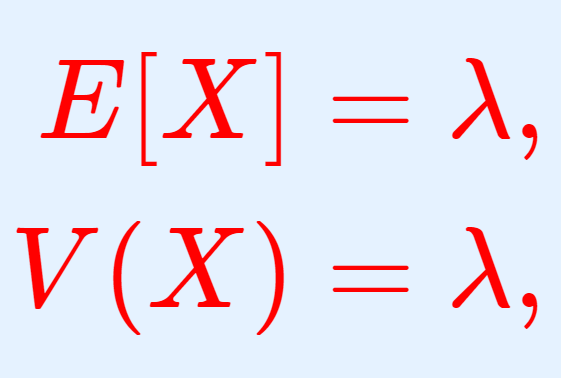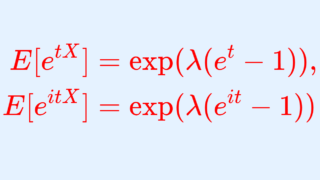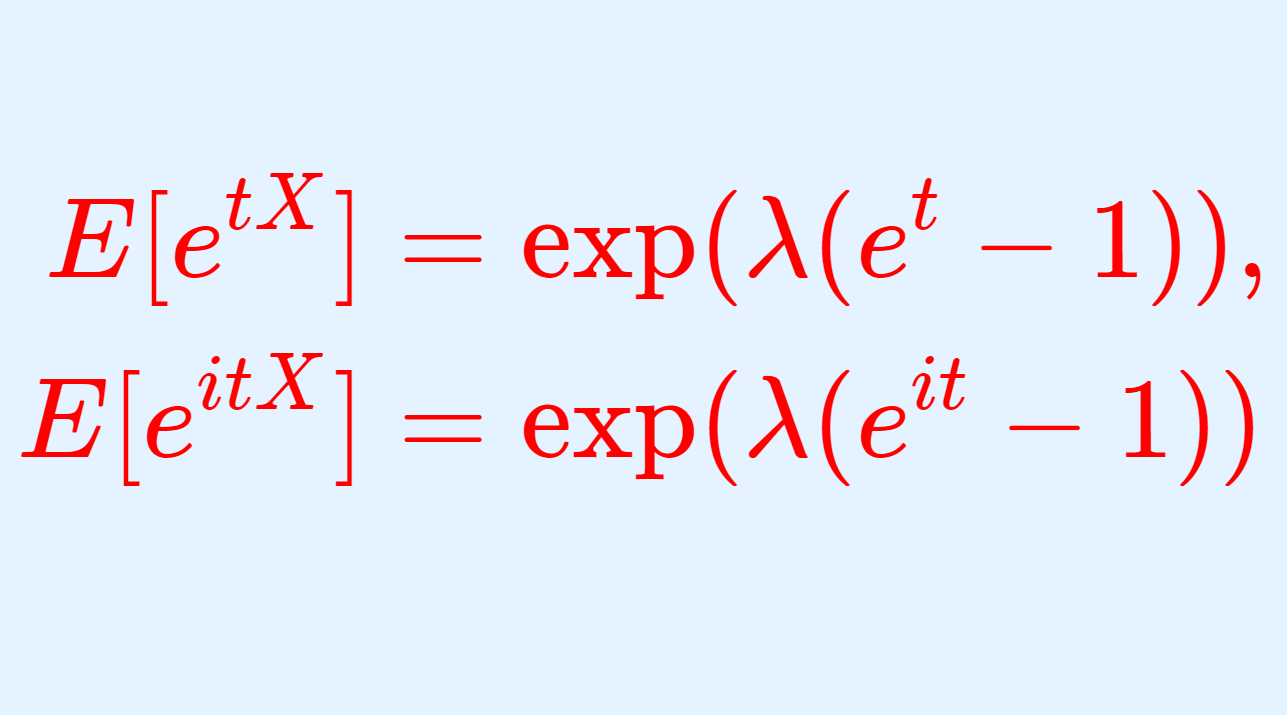ポアソン分布の期待値(平均)・分散・標準偏差はそれぞれ
\begin{aligned} E[X] &= \lambda, \\ V(X)&= \lambda, \\ \sqrt{V(X)} &= \sqrt{\lambda} \end{aligned}
となります。これについて,その導出証明を「定義から直接証明」「特性関数の微分を用いた証明」の2通りで行いましょう。
ポアソン分布の期待値(平均)・分散・標準偏差
まずは,もう一度結果をまとめましょう。
定理(ポアソン分布の期待値・分散・標準偏差)
X\sim \operatorname{Poisson}(\lambda) とする。このとき,X の期待値(平均)・分散・標準偏差はそれぞれ
\color{red}\begin{aligned} E[X] &= \lambda, \\ V(X)&= \lambda, \\ \sqrt{V(X)} &= \sqrt{\lambda} \end{aligned}
となる。
期待値も分散も,両方 \lambda になるんですね。
証明に入る前に,ポアソン分布の定義を復習しておきましょう。
X を確率変数, \lambda > 0 とする。 k=0,1,2,\ldots に対し,
\color{red} P(X=k) = \frac{\lambda^k}{k!}e^{-\lambda }
が成り立つとき, X はパラメータ \lambda のポアソン分布 (Poisson distribution) に従うという。本記事では,これを \color{red}X\sim \operatorname{Poisson}(\lambda) とかくことにする。
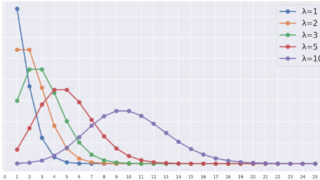
ポアソン分布は,「まれな事象が一定期間に起こる回数」をモデル化するのによく使います。詳しくは,以下の記事を参照してください。
ポアソン分布の期待値(平均)の導出証明
ポアソン分布の期待値(平均)の導出証明について,
- 定義から直接証明
- 特性関数の微分を用いた証明
の2種類で証明しましょう。
【期待値】定義から直接証明
定義から直接証明するには, e^x のマクローリン展開
e^x = \sum_{n=0}^\infty \frac{x^n}{n!},\quad x\in \mathbb{R}
を利用します。
証明
期待値とポアソン分布の定義より,
\begin{aligned} E[X] &= \sum_{k=0}^\infty k P(X=k) \\ &= \sum_{k=1}^\infty k \frac{\lambda^k}{k!}e^{-\lambda } \\ &= \sum_{k=1}^\infty \frac{\lambda^k}{(k-1)!}e^{-\lambda } \\ &= \lambda e^{-\lambda} \sum_{k=1}^\infty \frac{\lambda^{k-1}}{(k-1)!} \\ &= \lambda e^{-\lambda}e^{\lambda} = \lambda \end{aligned}
より,示せた。
証明終
【期待値】特性関数の微分を用いた証明
特性関数の微分を用いても,ポアソン分布の期待値を計算することが可能です。証明の前に,ポアソン分布の特性関数の結果を述べましょう。
これを微分する形で証明します。
証明
特性関数の式を両辺 t で微分すると,
E[iXe^{itX}] = i\lambda \exp(\lambda(e^{it}-1)+it) .
両辺 t=0 を代入すると, E[iX] = i\lambda であり,よって,
E[X] = \lambda.
証明終
なお,今回は特性関数を微分しましたが,積率母関数(モーメント母関数)を微分しても証明可能です。
ポアソン分布の分散の導出証明
ポアソン分布の分散の導出証明についても,
- 定義から直接証明
- 特性関数の微分を用いた証明
の2種類で証明しましょう。 V(X) =E[X^2] -E[X]^2 を用います。
【分散】定義から直接証明
証明
まずは二次モーメント E[X^2] について,ポアソン分布の定義から,
\begin{aligned}&E[X^2]\\ &= \sum_{k=0}^\infty k^2 P(X=k) \\ &= \sum_{k=1}^\infty k^2 \frac{\lambda^k}{k!}e^{-\lambda } \\ &= \sum_{k=1}^\infty \{k(k-1)+k\} \frac{\lambda^k}{k!}e^{-\lambda } \\ &= e^{-\lambda}\left\{ \sum_{k=2}^\infty \frac{\lambda^k}{(k-2)!}+\sum_{k=1}^\infty \frac{\lambda^k}{(k-1)!} \right\} \\ &= e^{-\lambda} \left\{ \lambda^2 \sum_{k=2}^\infty \frac{\lambda^{k-2}}{(k-2)!} + \lambda\sum_{k=1}^\infty \frac{\lambda^{k-1}}{(k-1)!} \right\} \\ &= e^{-\lambda} (\lambda^2 e^{\lambda} + \lambda e^{\lambda} )\\ &= \lambda^2 +\lambda \end{aligned}
であるから,
証明終
【分散】特性関数の微分を用いた証明
証明
特性関数の式 E[e^{itX}]= \exp(\lambda(e^{it}-1)) の両辺を t で2回微分すると,
\begin{aligned} & E[(iX)^2 e^{itX}] \\ &= -\lambda (\lambda e^{it}+1)\exp(\lambda(e^{it}-1)+it) . \end{aligned}
両辺 t=0 を代入すると, E[(iX)^2] = -\lambda(\lambda+1) すなわち,
よって, V(X) = E[X^2] - E[X]^2 = (\lambda^2 + \lambda)-\lambda^2 = \lambda である。
証明終
ポアソン分布の標準偏差について
標準偏差は,分散の平方根 \sqrt{V(X)} で定義されます。上の計算より, V(X0 = \lambda でしたから,
\sqrt{V(X)} = \sqrt{\lambda}
が分かりますね。