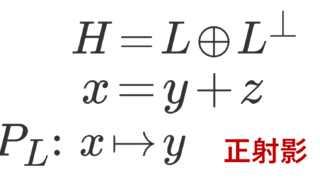ヒルベルト空間において非常に基本的な定理である射影定理 (projection theorem) について,その定理の主張と証明を行いましょう。
ヒルベルト空間における射影定理
実あるいは複素ヒルベルト空間 H に対して,A\subset H が凸集合 (convex set) であるとは,
\color{red}x,y\in A\implies tx+(1-t)y\in A\quad(0\le t\le 1)
を意味します(→凸集合とは何かをわかりやすく~定義と性質~)。このことを踏まえて,定理を述べましょう。
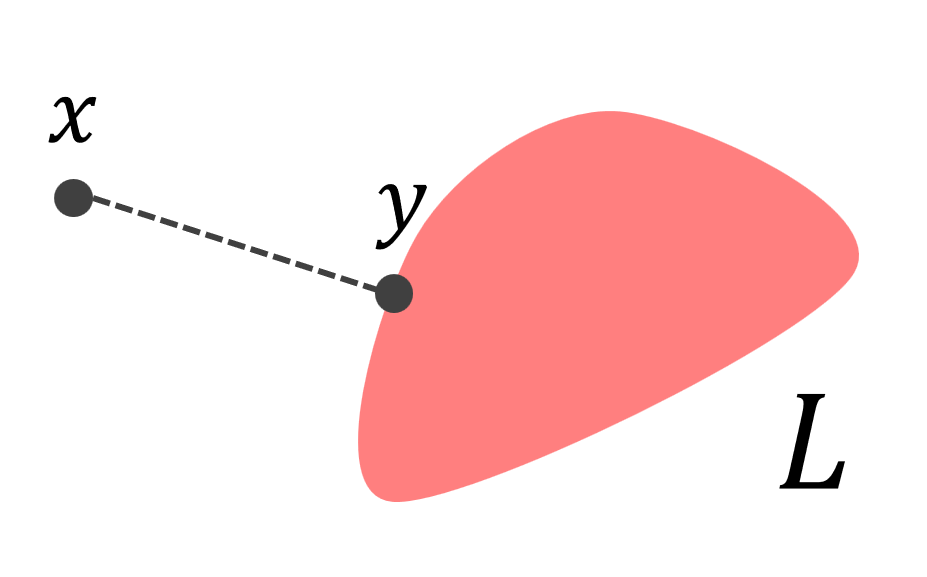
定理1 (射影定理)
H をヒルベルト空間とし, A\subset H を空でない閉凸集合とする。このとき,任意の x\in X に対して,
\color{red} \Large\|x-y\| =\inf_{a\in A} \|x-a\|
となる y\in A が唯一つ存在する。また, A が閉部分空間ならば, x-y\perp A である。
x\in A なら,単に y=x とすればよいです。
x-y\perp A とは,\forall a\in A, \langle x-y, a\rangle =0 の意味です。
閉部分空間は明らかに閉凸集合ですから,定理1の「閉凸集合」の部分は「閉部分空間」にしても成立します。x = y+(x-y) であり,y\perp x-y ですから,さらに以下の定理が成立します。
定理2(射影定理2)
H をヒルベルト空間, L\subset H をその閉部分空間とする。また,
L^\perp=\{ x\in H\mid \langle x,y\rangle =0,\, \forall y\in L\}
を L の直交補空間とする。このとき,任意の x\in H に対し,
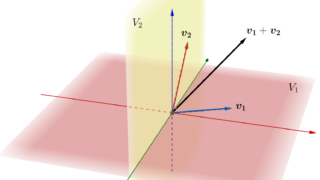
となる y,z が唯一つ存在する。特に,\large\color{red} H= L\oplus L^{\perp} である(→ベクトル空間の和・直和の定義)。
直交補空間については,以下の記事でも掘り下げています。
定理1と2はどちらも射影定理と言われます。
射影定理の証明
さて,早速証明しましょう。
H をヒルベルト空間とし, A\subset H を空でない閉凸集合とする。このとき,任意の x\in X に対して,
\color{red} \Large\|x-y\| =\inf_{a\in A} \|x-a\|
となる y\in A が唯一つ存在する。また, A が閉部分空間ならば, x-y\perp A である
- y の存在性について
- y の一意性について
- A が閉部分空間のとき x-y\perp A について
に分けて証明していきましょう。どれもある程度テクニカルであり,証明も大事ですが,結果を身につけることがとても大切です。
定理1の証明
1. y の存在性について
\inf_{a\in A} \|x-a\|=\alpha とおく。下限(inf)の定義より, \{y_n\}\subset A で, \lim_{n\to\infty}\|x-y_n\| =\alpha となるものが存在する。中線定理も用いることで,
\begin{aligned} &\|y_m-y_n\|^2 \\&= \|(y_m-x)-(y_n-x)\|^2 \\ &=2(\|y_m-x\|^2+\|y_n-x\|^2)\\ &\qquad-\|(y_m-x)+(y_n-x)\|^2 \\ &=2(\|y_m-x\|^2+\|y_n-x\|^2)\\ &\qquad\qquad\quad-4\left\|\frac{y_m+y_n}{2}-x\right\|^2 \\ \end{aligned}
である。 A は凸より, \frac{y_m+y_n}{2}\in A である。ゆえに \alpha の定義より, |\frac{y_m+y_n}{2}-x\| \ge \alpha である。したがって,
となり, \{y_n\} はコーシー列である。ゆえに y_n\xrightarrow{n\to\infty} y\in H が存在し, A は閉より, y\in A である。ここで,
より, \|x-y\|=\alpha である。以上から存在性が示せた。
2. y の一意性について
y_1,y_2\in A が \|x-y_1\| = \|x-y_2\| = \alpha をみたすとする。中線定理より,
\hspace{-10pt}\begin{aligned}&\| (x-y_1)+(x-y_2)\|^2+\| (x-y_1)-(x-y_2)\|^2 \\&=2(\|x-y_1\|^2 +\|x-y_2\|^2) . \end{aligned}
言い換えると,
A は凸より, \frac{y_1+y_2}{2}\in A なので, \alpha の定義より, \| x-\frac{y_1+y_2}{2}\|\ge \alpha である。よって,上式は
したがって, y_1=y_2 となって,一意性が示せた。
3. A が閉部分空間のとき x-y\perp A について
z=x-y と略記する。 a\in A とし,さらに \rho = \langle z, a\rangle とする。 \rho=0 を示せばよい。 t\in \mathbb{C} について, t\rho a\in A である。 \varphi(t)=\|z-t\rho a\| と定めると,\|x-y\| の最小性より, \varphi(0)\le \varphi(t) である。 一方で, t\in \R なら,
\|z-t\rho a\|^2= \|z\|^2-2|\rho|^2t+|\rho|^2\|a\|^2t^2
となるため, \rho=0 でなければ \varphi(0)\le \varphi(t) に矛盾する。
証明終
H をヒルベルト空間, L\subset H をその閉部分空間とする。また,
L^\perp=\{ x\in H\mid \langle x,y\rangle =0,\, \forall y\in L\}
を L の直交補空間とする。このとき,任意の x\in H に対し,
となる y,z が唯一つ存在する。特に,\large\color{red} H= L\oplus L^{\perp} である(→ベクトル空間の和・直和の定義)。
定理2の証明
存在性については,定理1より明らか。
一意性について
x=y_1+z_1=y_2+z_2,\;\; y_1,y_2\in L,\, z_1,z_2\in L^\perp とする。このとき, y_1-y_2=z_2-z_1 \in L\cap L^\perp = \{0\} であるから, y_1=y_2,\, z_1=z_2 となり,一意である。
証明終
一意性の証明は,ベクトル空間の和・直和の定義とその次元の等式の証明での証明と同じで,一般のベクトル空間でも成立します。