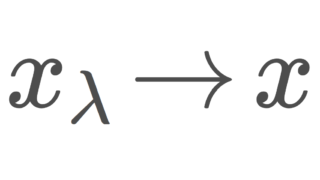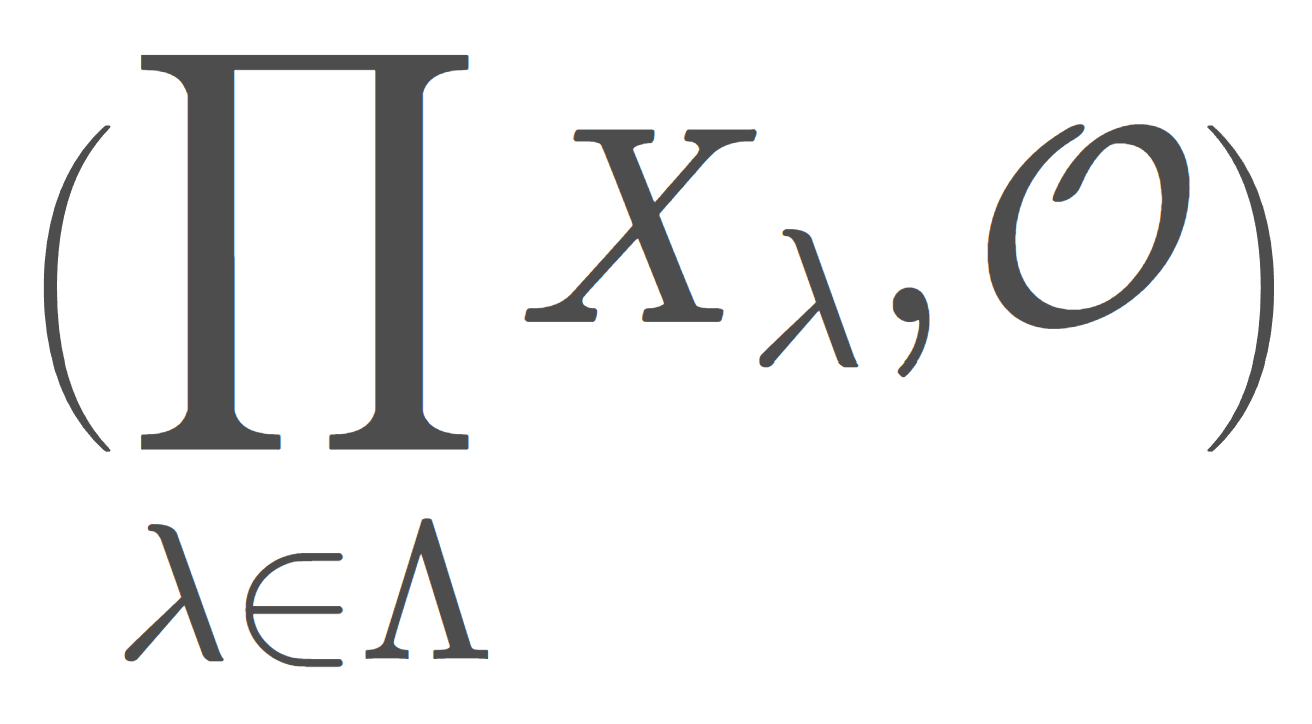相対コンパクトとは，閉包がコンパクトになるような部分集合のことを言います。
相対コンパクトについて，その定義と具体例，さらにはネット(有向点族)・点列との関係性まで紹介しましょう。
相対コンパクトの定義
定義（相対コンパクト）
(X,\mathcal{O}) を位相空間とし， A\subset X とする。
閉包 \overline{A} がコンパクト集合であるとき， A は相対コンパクト (relatively compact) であるという。
「閉包がコンパクト」と言いたい場面は多いですが，毎回「閉包がコンパクト」というのもアレなので，「相対コンパクト」と言おう，という感じです。英語でも，its closure is compact というより，relatively compact と言った方が良さげですね。
ちなみに， A が相対コンパクトであることを，記号で A\Subset X とかくこともあります。
相対コンパクトの例・そうでない例
一般には，相対コンパクトだからといってコンパクトとは言えないし，逆にコンパクトだからといって相対コンパクトとも言えません。確認しましょう。
例1( \R).
通常の位相が入った実数 \R の空間について， a<b とすると，
- [a,b] はコンパクトかつ相対コンパクトである
- (a,b) はコンパクトでないが，相対コンパクトではある
- A\subset \R が相対コンパクトである必要十分条件は， A が有界集合であることである。
A\subset \R がコンパクトである必要十分条件は， A が有界閉集合であることです。
例2(特定点位相).
X を無限集合とし， x\in X とする。
\mathcal{O}=\{ O\subset X\mid x\in O\}\cup \{\emptyset\}
を， x を含む部分集合族(と \{\emptyset\} の和集合)とすると， (X,\mathcal{O}) は位相空間となる。
このとき，\{x\} は1点集合なのでコンパクトであるが，相対コンパクトではない
\overline{\{x\}}=X であり， X は今はコンパクトではないので， \{x\} は相対コンパクトではありません。
例3(密着位相).
(X,\{ \emptyset, X\}) を密着空間とするとき，任意の部分集合 A\subset X はコンパクトかつ相対コンパクトである。
A\subset X の開被覆は \{X\} しかなく，これは \overline{A}=X の開被覆にもなっています。
相対コンパクトの性質
相対コンパクトの性質について，コンパクトとの関係性と，ネット(有向点族)や点列との収束の関係性について述べましょう。
コンパクトと相対コンパクトの関係性
一般には相対コンパクトだからといってコンパクトとは言えないし，逆にコンパクトだからといって相対コンパクトとは言えないことを確認しました。実際はもう少し仮定を増やすと，これらには関係性があります。
定理1（コンパクトと相対コンパクトの関係性）
(X,\mathcal{O}) を位相空間とする。このとき，
証明
1.について コンパクト集合の閉部分集合は常にコンパクトであるから，任意の部分集合は相対コンパクトである。
2.について ハウスドルフ空間のコンパクト集合は閉集合である。よって， A がコンパクトなら A は閉集合なので，相対コンパクトでもある。
証明終
収束と相対コンパクトの関係性
ネット(有向点族)や点列の収束と，相対コンパクトの関係性を述べましょう。
定理2（ネット(有向点族)の収束と相対コンパクトの関係性）
(X,\mathcal{O}) を位相空間とし， A\subset X を空でないとする。
- A がコンパクト \iff 任意のネット (x_\lambda)\subset A が A 内に収束する部分ネットを持つ
- A が相対コンパクト \implies 任意のネット (x_\lambda)\subset A が収束する部分ネットを持つ
証明
1.については，コンパクト空間とコンパクト集合について詳しくの中で証明している。
2.について， \overline{A} はコンパクトである。よって1.より，ネット (x_\lambda)\subset A\subset \overline{A} は， \overline{A} 内に収束する部分ネットをもつ。
証明終
なお，一般に2.の逆( \impliedby 方向)は成立しません。これは例2.からわかります。実際，例2.において，任意のネット (x_\lambda)\subset \{x\} は定ネットなので x に収束しますが，\overline{\{x\}}=X はコンパクトでなく， X は全体空間なので， \overline{X}=X であり，相対コンパクトではないとわかります。
距離空間なら，ネット(有向点族)の議論は点列の議論に置き換えても大丈夫です。以下が成り立ちます。
定理3（点列の収束と相対コンパクトの関係性）
(X,d) を距離空間とし， A\subset X を空でないとする。
- A がコンパクト \iff 任意の点列 (x_n)\subset A が A 内に収束する部分点列を持つ
- A が相対コンパクト \iff 任意の点列 (x_n)\subset A が収束する部分点列を持つ
2.で \impliedby が成り立つのがポイントです。距離空間において相対コンパクトを示すのに，任意の点列が収束部分列を持つことはよく使います。
2.の \impliedby の証明
\overline{A} がコンパクトであることを示せばよい。1.より，任意の点列 (x_n)\subset \overline{A} が収束部分列をもつことを示せばよい。
x_n\in \overline{A} より， B_{1/n}(x_n)\cap A \ne \emptyset である。ただし，
B_{1/n} (x_n)= \{ y\in X\mid d(y, x_n)<1/n\}
は， x_n の周りの 1/n-近傍とする。よって， y_n\in B_{1/n}(x_n)\cap A を選ぶことができ，これにより，点列 (y_n)\subset A が取れる。2.の仮定より，収束部分列 (y_{n_k})\subset A が取れる。 y_{n_k}\xrightarrow{k\to\infty} y\in \overline{A} とする。
このとき， \varepsilon >0 に対し，ある K\ge 1 が存在して，
k\ge K\implies d(y_{n_k}, y)< \frac{\varepsilon}{2},\quad \frac{1}{k}<\frac{\varepsilon}{2}
とできる。このとき， k\ge K に対し，
となるから， x_{n_k}\xrightarrow{k\to\infty} y である。ゆえに， (x_n) が収束部分列をもつことが示された。
証明終
コンパクトに関連する概念
最後に，コンパクトに関係する概念を紹介しましょう。用語は
L. A. Steen, J. A. Seebach, Counterexamples in Topology, 2nd edition. Springer, 1978.
にならっています。
| 名称 | 定義 |
|---|---|
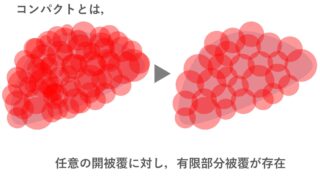
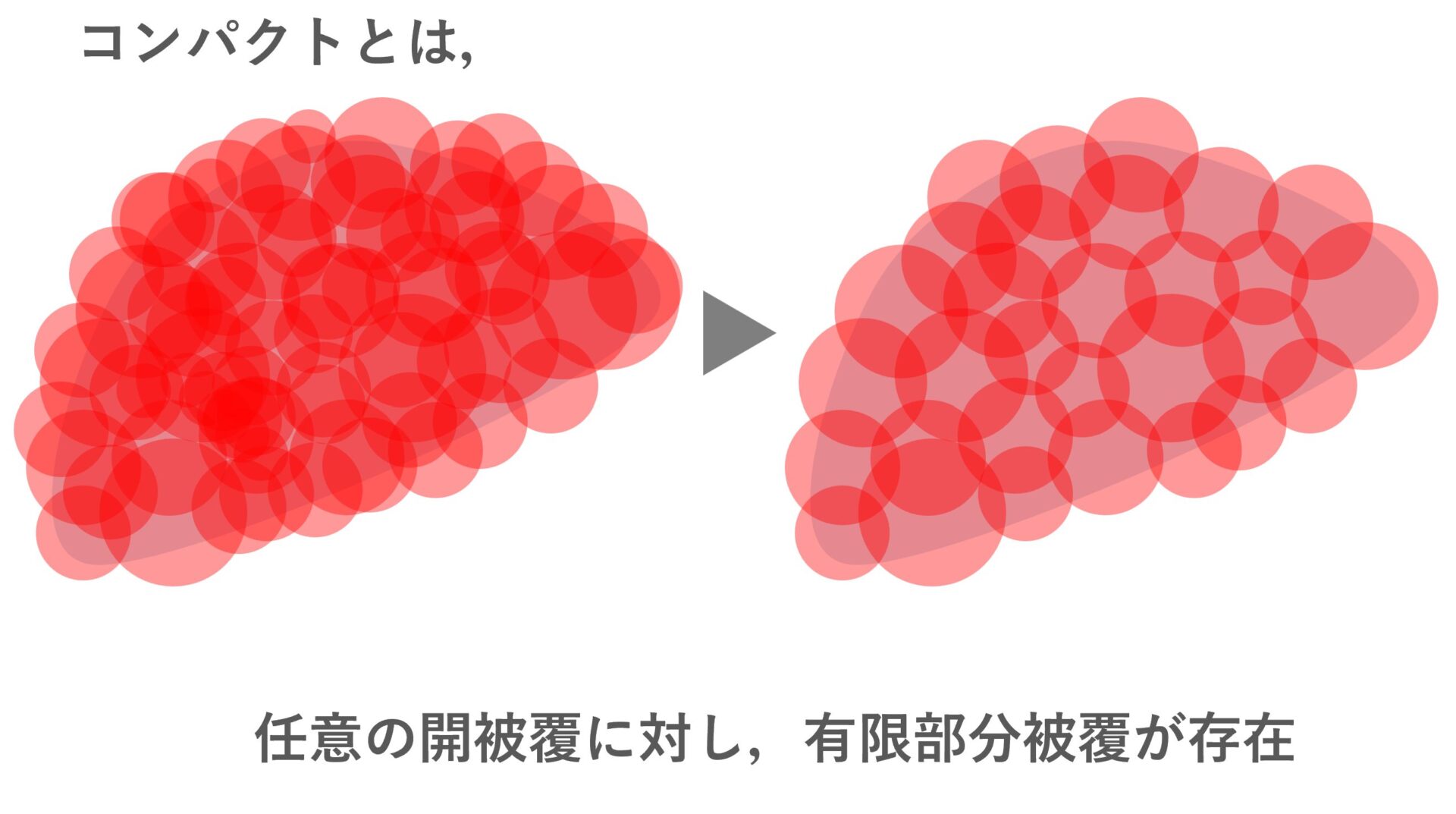
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| 強局所コンパクト (strong locally compact) | 任意の点がコンパクトな閉近傍をもつ |
| 相対コンパクト (relatively compact) | 閉包がコンパクトな部分集合 |
| 可算コンパクト (countably compact) | 任意の可算開被覆が有限部分被覆をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち，各点ごとに有限個の集合でしか覆われていない)部分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち，各点ごとに有限個の集合でしか覆われていない近傍をもつような)部分被覆をもつ |
