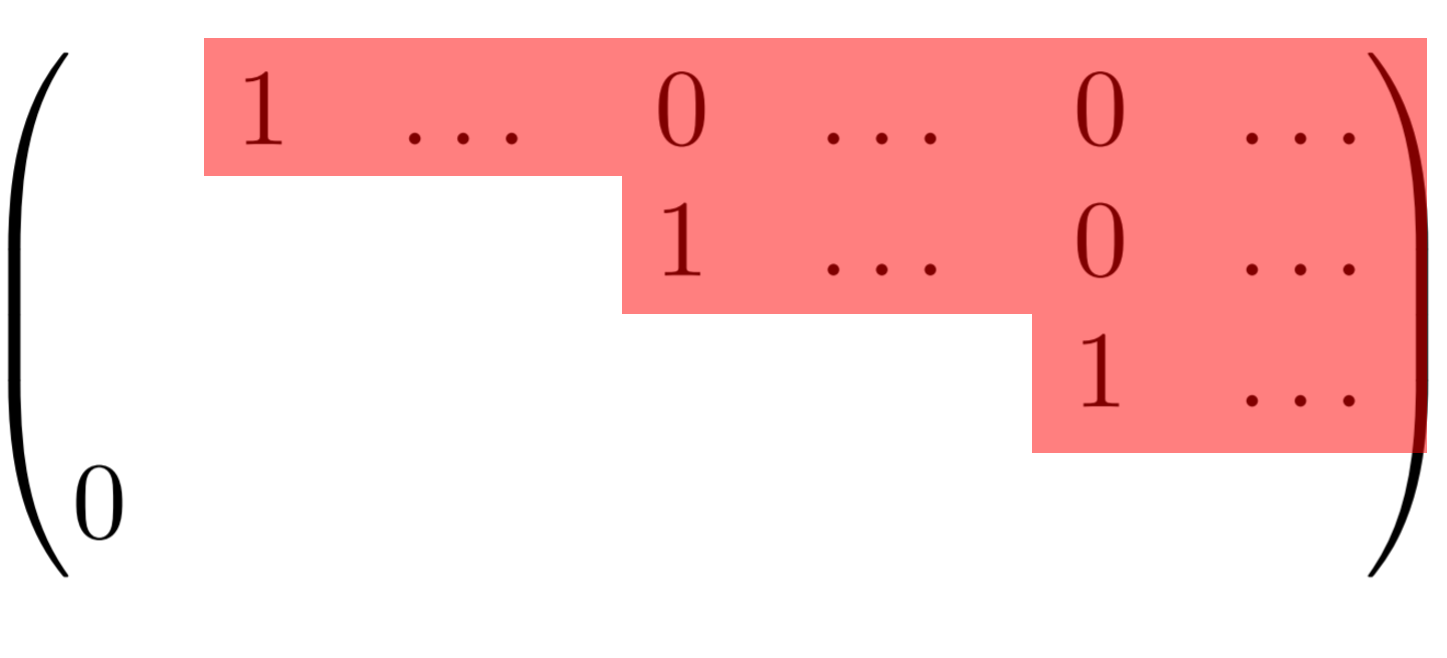
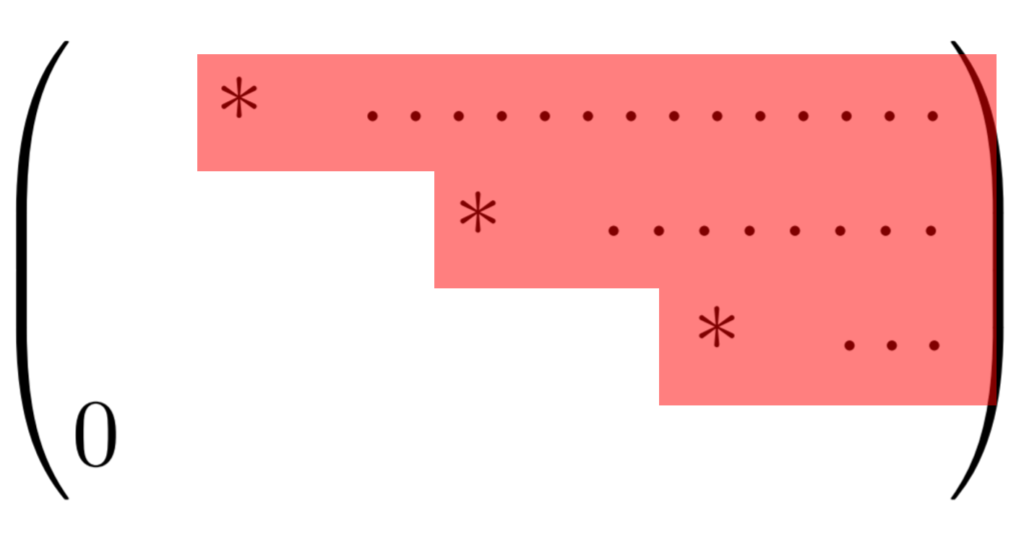
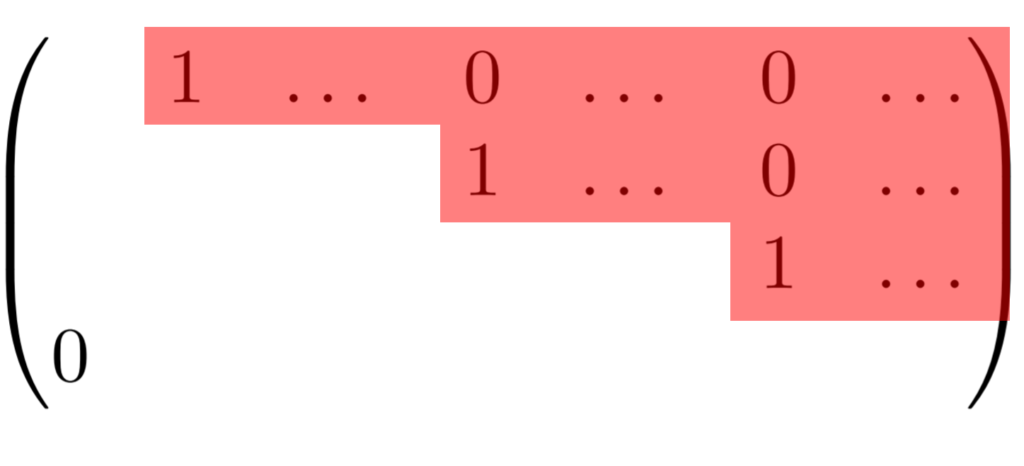
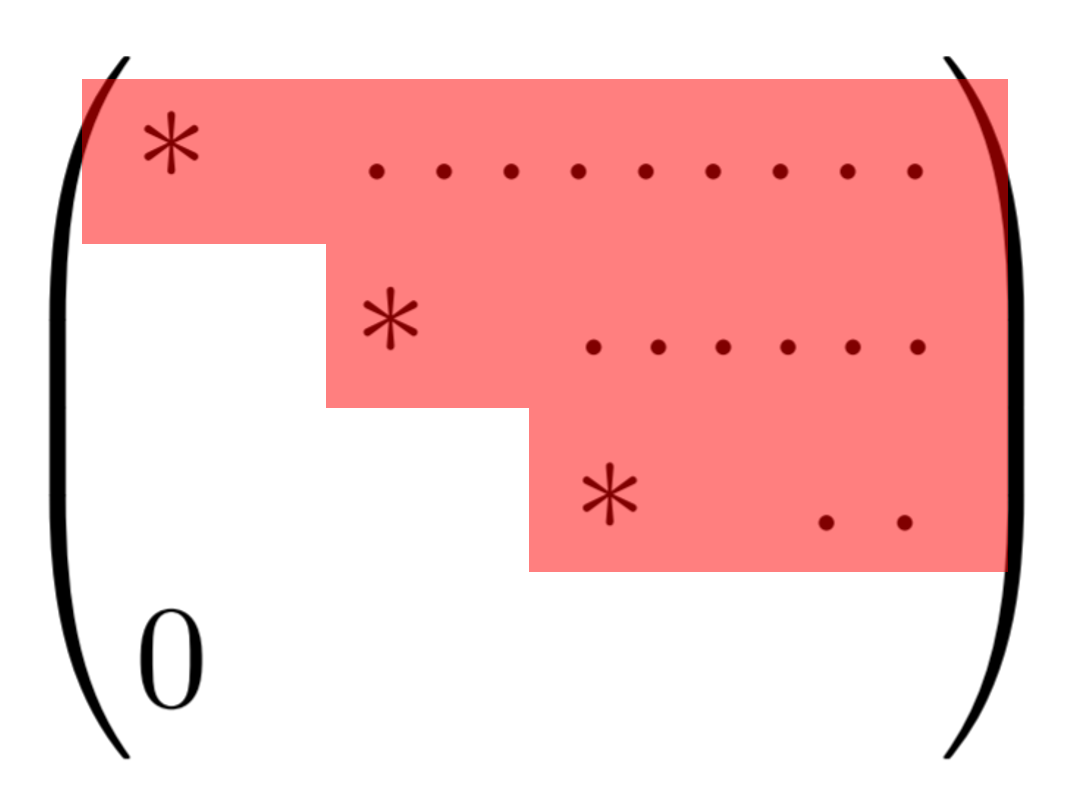
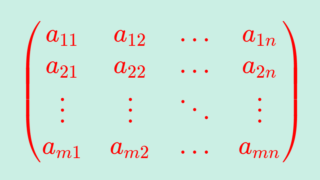階段行列のうち,特別な形のものをRREF行列 (Reduced row echelon form) といい,この行列に変形することを,「行列の簡約化」といいます。これの定義と,その求め方を分かりやすく紹介します。
【行列の簡約化】RREF行列の定義
RREF行列は階段行列の特殊なものなわけですね。
RREF行列の具体例
RREF行列の具体例を挙げましょう。
例
- \begin{pmatrix} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & 1 \end{pmatrix}
- \begin{pmatrix} 1 & 2 & 0 & -1 & 0 \\ 0 & 0 & 1 & 2 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{pmatrix}
- \begin{pmatrix} 0 & 1 & 0 & 2 \\ 0 & 0 & 1 & 2 \\ 0 & 0 & 0 & 0 \end{pmatrix}
- \begin{pmatrix} 1 & 0 & 2 & 0 \\ 0 & 1 & 2 & 0 \end{pmatrix}
- \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ 0 & 0 \\ 0 & 0\end{pmatrix}
- 単位行列
【行列の簡約化】RREF行列の行基本変形を用いた求め方
RREF行列を,行基本変形のみを用いて求める方法を紹介します。これを,行列の簡約化といいます。求め方は以下の通りです。
- 行基本変形を用いて階段行列に直す
- 階段行列に対して, * を 1 に,その上が 0 になるように行基本変形を行う
1.の階段行列を得るところまでは,階段行列の求め方と全く一緒なので,以下の記事を参照してください。
今回は,2.のステップのみ,例を交えて紹介することにしましょう。
例題
\begin{pmatrix} 1 & 1& 3& 5\\ 0 & 1& 1& -2 \\ 0 & 0 & 9 & 7 \end{pmatrix} を,行基本変形を用いてRREF行列に変形せよ。
解答を確認してみましょう。方針としては,残すべき「1」の上すべてが「0」になるように足し引きを行います。