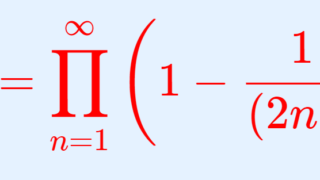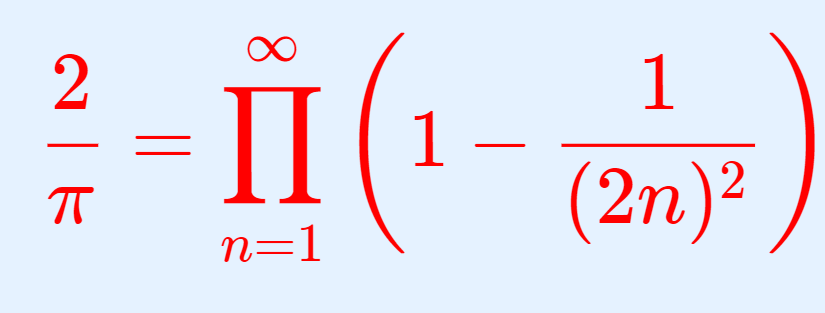n! の近似公式であるスターリングの公式 \displaystyle n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n を紹介し,証明しましょう。
スターリングの公式
定理(スターリングの公式; Stirling’s formula)
\color{red} n! \sim \sqrt{2\pi n} \left(\frac{n}{e}\right)^n.
ここで, f(x) \sim g(x) とは, f(x)/g(x) \xrightarrow{x\to\infty} 1 を意味する。
ここでの「近似」とは,両者の比が 1 に収束することを指します。すなわち,
\lim_{n\to\infty} \frac{n!}{\sqrt{2\pi n} \left(\frac{n}{e}\right)^n} = 1
ということですね。早速証明していきましょう。
スターリングの公式の厳密な証明
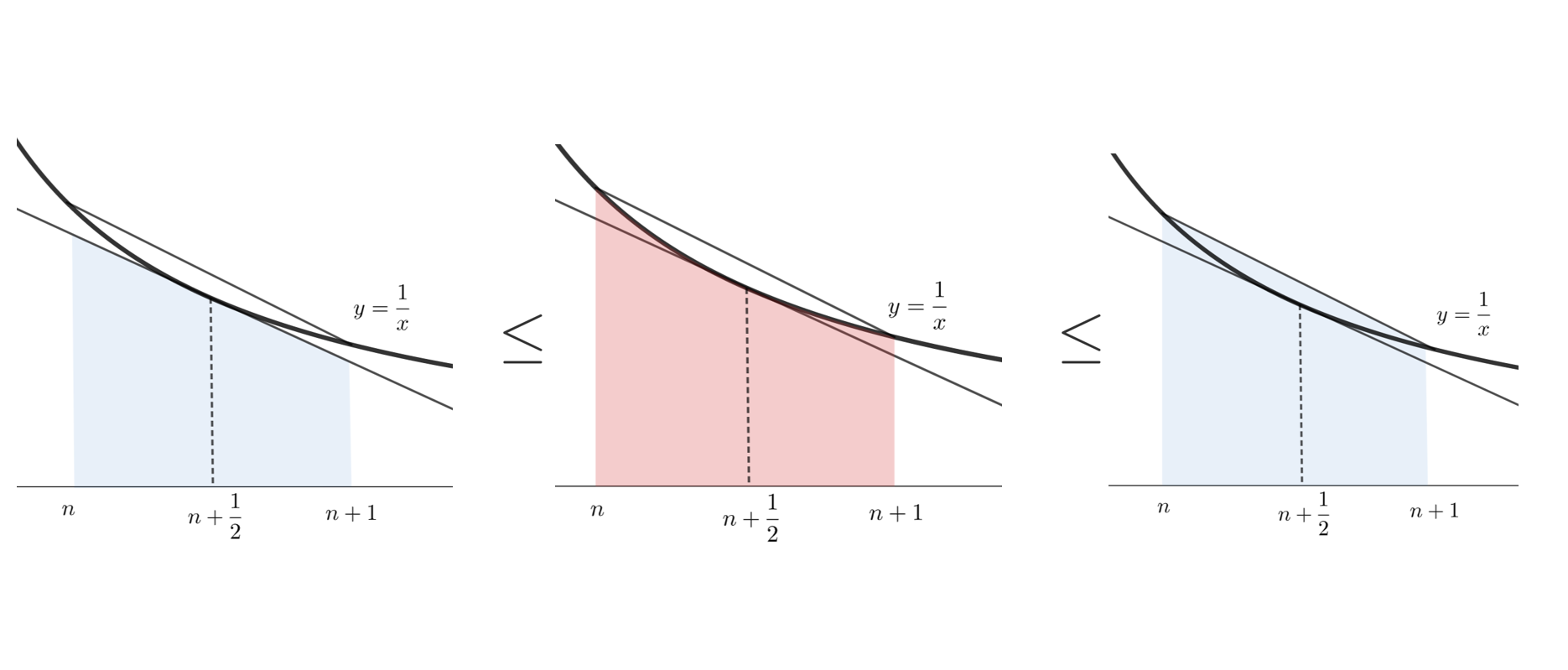
証明にはウォリスの公式を用います。ウォリスの公式をかいておきましょう。
ウォリスの公式自体の証明は,以下の記事で解説しています。
これを用いて証明してみましょう。
証明
a_n = \dfrac{n!}{ \sqrt{n}\left(\frac{n}{e}\right)^n} とおいて, a_n \xrightarrow{n\to\infty} \sqrt{2\pi} を示せばよい。
\begin{aligned} \log \frac{a_n}{a_{n+1}}&= \log a_n - \log a_{n+1} \\ &=\left(n+\frac{1}{2}\right) \log\left(1+\frac{1}{n}\right) - 1 \\ &= \left(n+\frac{1}{2}\right) \int_n^{n+1} \frac{dx}{x} - 1 \end{aligned}
であり, y=\frac{1}{x} は凸であるから,面積の比較により,
\frac{1}{n+1/2} \le \int_n^{n+1} \frac{dx}{x} \le \frac{1}{2}\left( \frac{1}{n} + \frac{1}{n+1} \right).
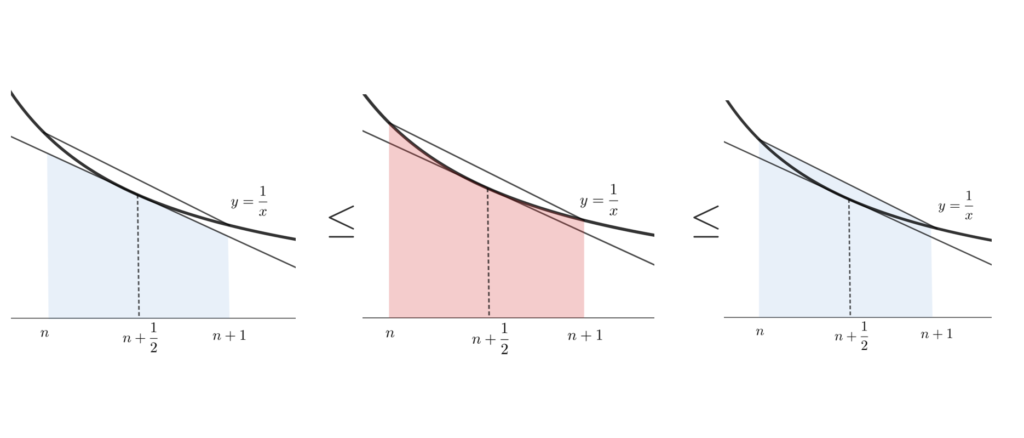
従って, 0 \le \log a_n/a_{n+1} \le 1/4n(n+1). であり,各辺 \sum_{n}^{2n-1} とすることで,
これより, a_n/a_{2n} \xrightarrow{n\to\infty} 1.
ここで,
\begin{aligned} \frac{a_n^2}{a_{2n}}&= \frac{2^{2n+1/2}}{\sqrt{n}} &=\sqrt{2} \frac{2^{2n}(n!)^2} {\sqrt{n}(2n)!} \end{aligned}
であり,両辺 n\to\infty とすると,ウォリスの公式から,
よって結論を得る。
証明終
若干天下りなような気もしますが,証明できましたね。