 測度論
測度論 【ヴィタリ集合】ルベーグ非可測集合の存在とその証明
ヴィタリ集合(vitali set)とは,剰余群R/Qにおける各代表元の集合を指し,選択公理を仮定することで存在が認められます。ヴィタリ集合はルベーグ非可測集合の例として有名です。ヴィタリ集合について,その構成とルベーグ非可測であることの証明を行いましょう。
 測度論
測度論  線形代数学
線形代数学  線形代数学
線形代数学  群・環・体
群・環・体  測度論
測度論  線形代数学
線形代数学  線形代数学
線形代数学 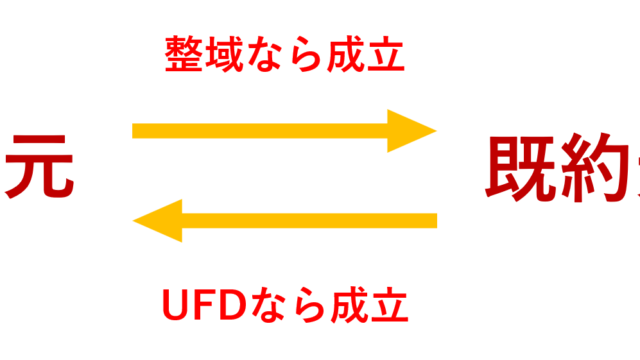 群・環・体
群・環・体 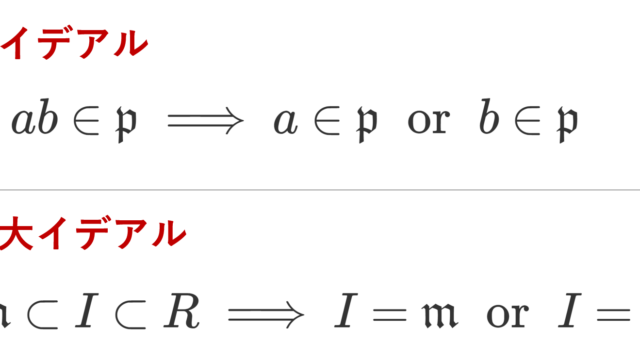 群・環・体
群・環・体 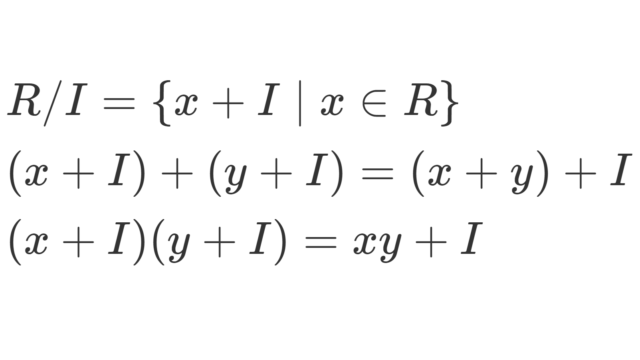 群・環・体
群・環・体