 解析学(大学)その他
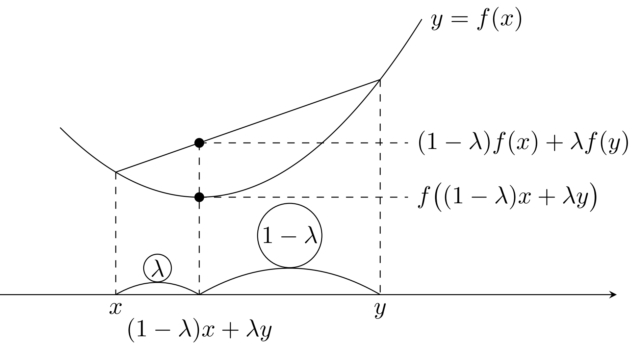
解析学(大学)その他 凸関数と凸不等式(イェンセンの不等式)についてかなり詳しく
凸関数 (convex function) は,それ自身が研究対象の一つであり,凸解析 (convex analysis) といわれることがあります。凸関数・凹関数と凸不等式(イェンセンの不等式)について,基本的なことを詳しくまとめましょう。
 解析学(大学)その他
解析学(大学)その他  群・環・体
群・環・体 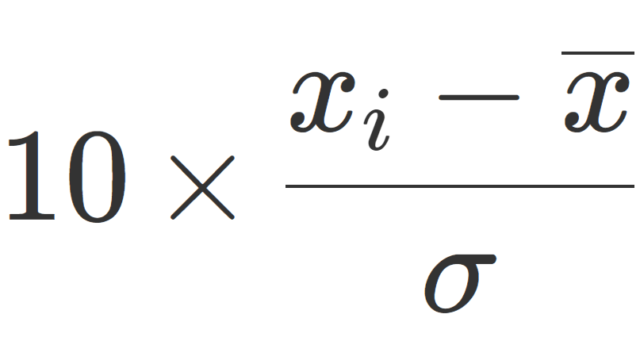 統計学
統計学  数論
数論 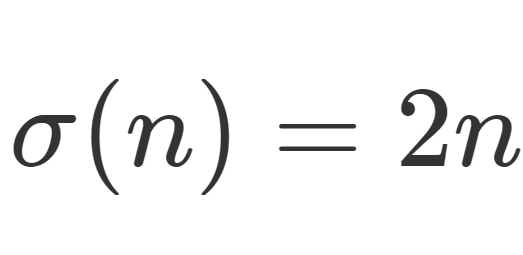 数論
数論 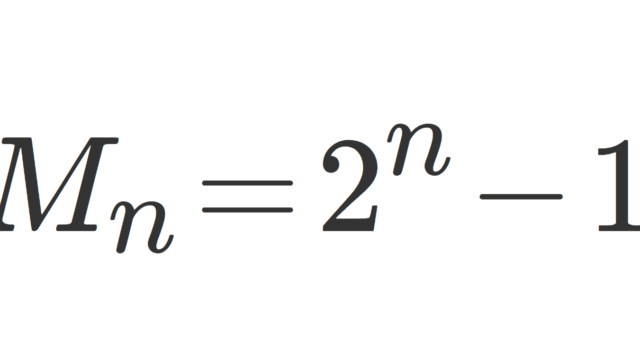 数論
数論 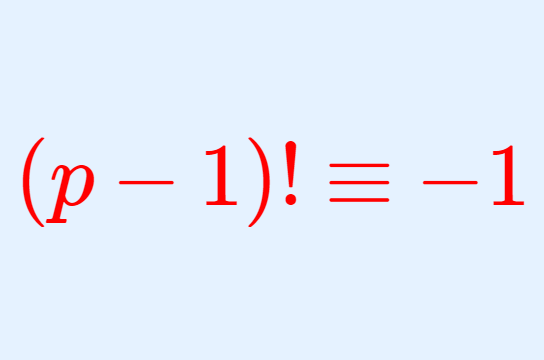 数論
数論 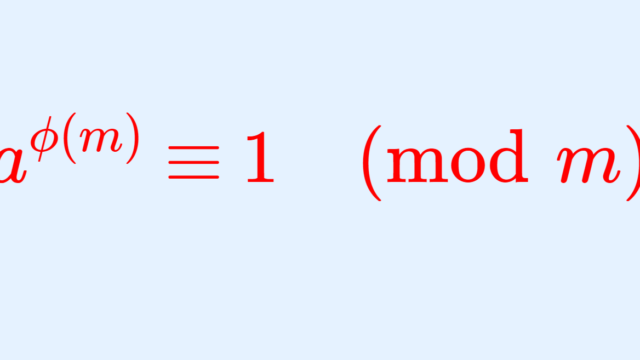 数論
数論 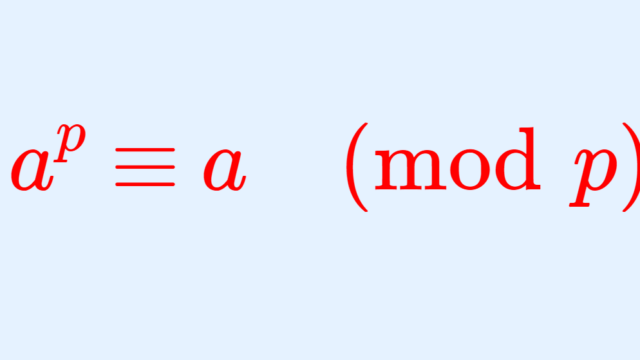 数論
数論  微分積分学(大学)
微分積分学(大学)