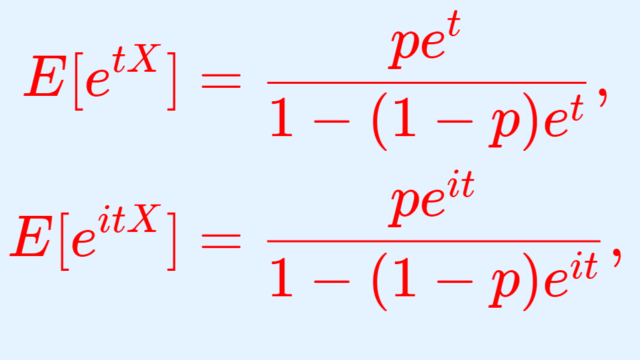 確率論
確率論 幾何分布のモーメント母関数・特性関数とその導出証明
幾何分布は,コインで初めて表が出る試行回数を表す離散型確率分布です。これについて,そのモーメント母関数(積率母関数)・特性関数の紹介と,その導出の証明を行いましょう。
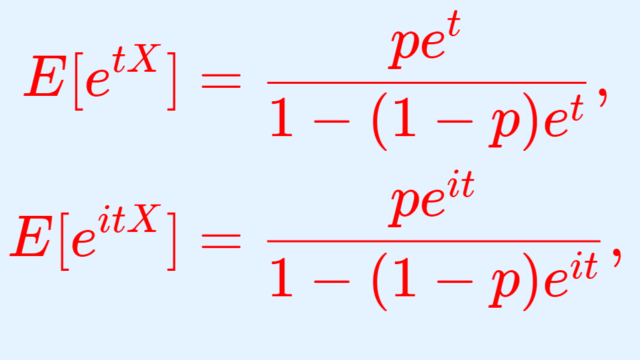 確率論
確率論 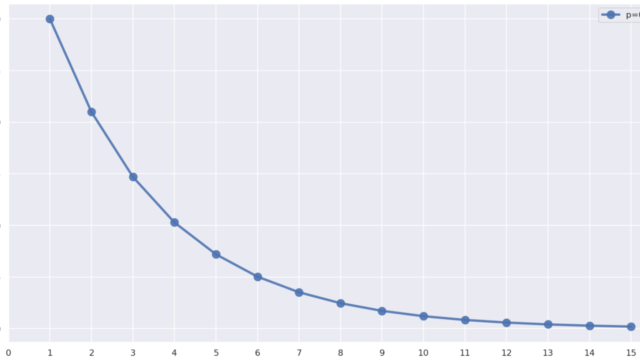 確率論
確率論 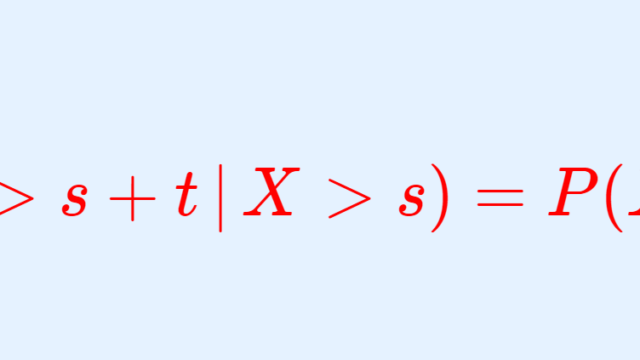 確率論
確率論 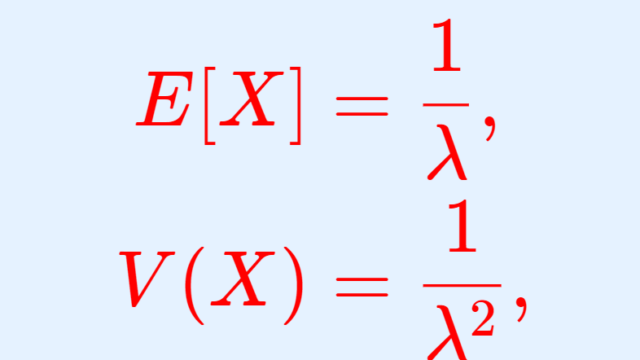 確率論
確率論 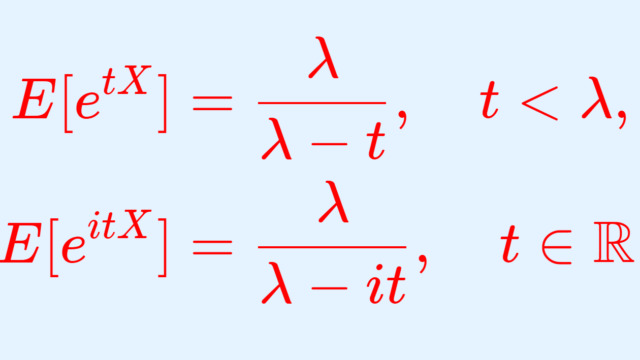 確率論
確率論 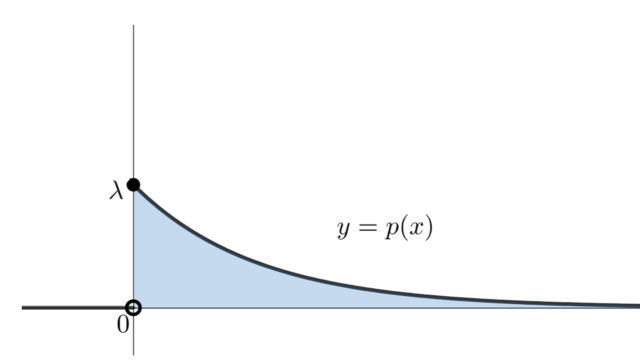 確率論
確率論 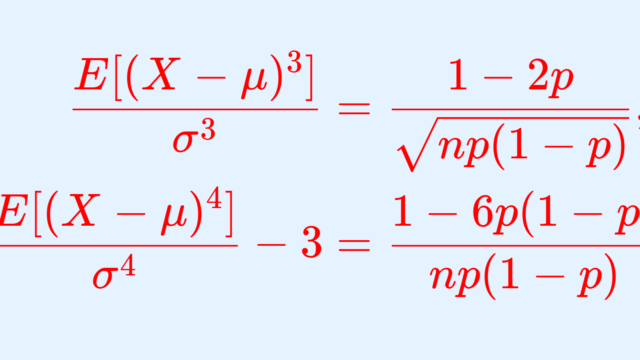 確率論
確率論 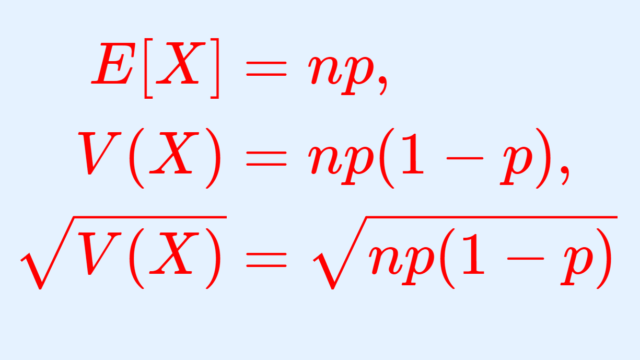 確率論
確率論 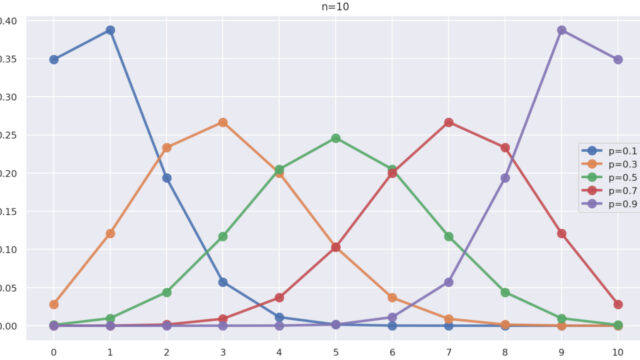 確率論
確率論  微分積分学(大学)
微分積分学(大学)