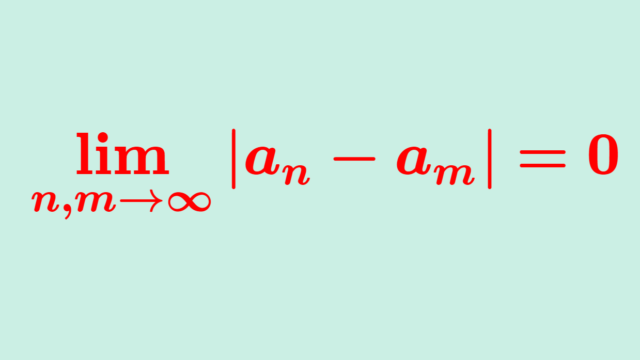 微分積分学(大学)
微分積分学(大学) 【微分積分学】コーシー列とは~定義と収束性の証明~
コーシー列(Cauchy sequence, 基本列)は,収束値は分からないが収束することが分かる,収束判定の道具といえます。これについて定義と,コーシー列であることと収束列であることが同値であるという定理の証明を行います。否定の紹介もします。
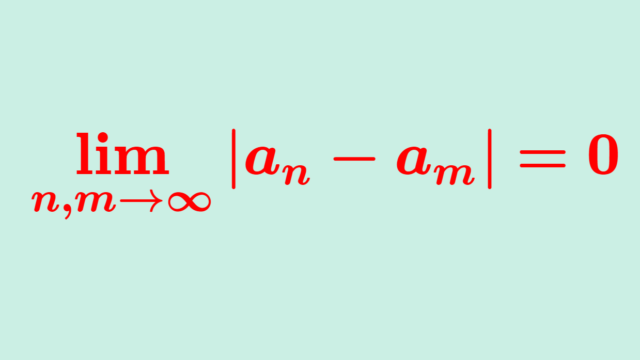 微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学)  微分積分学(大学)
微分積分学(大学) 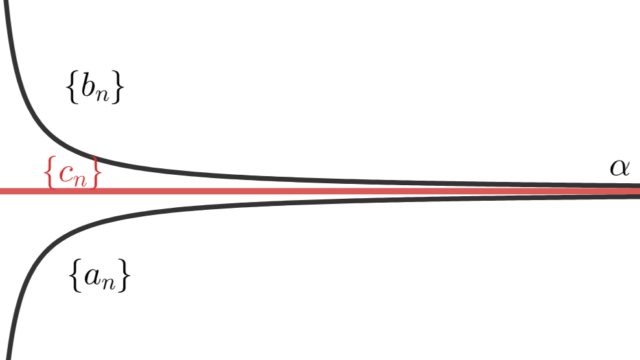 微分積分学(大学)
微分積分学(大学) 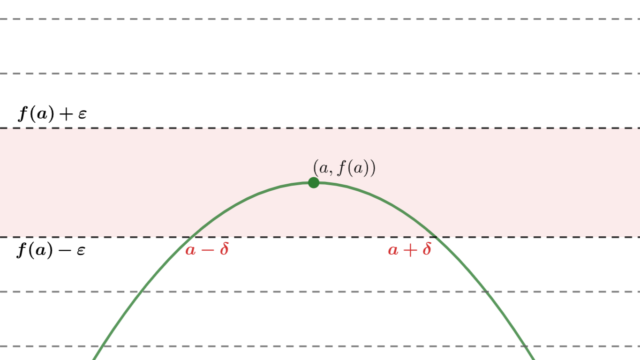 微分積分学(大学)
微分積分学(大学) 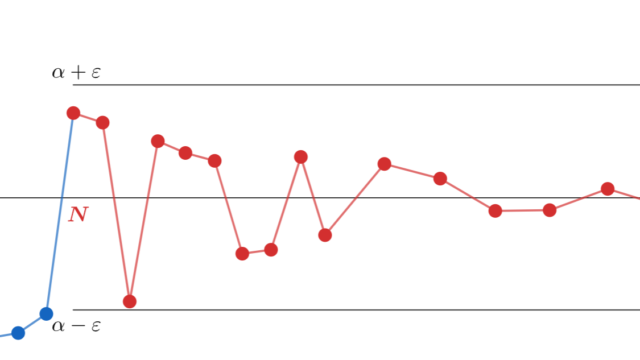 微分積分学(大学)
微分積分学(大学) 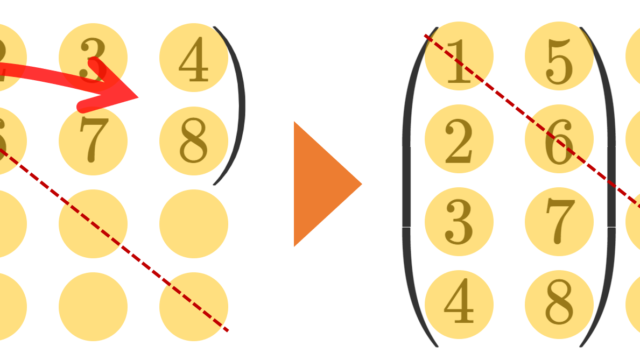 線形代数学
線形代数学  微分積分学(大学)
微分積分学(大学)  線形代数学
線形代数学  線形代数学
線形代数学