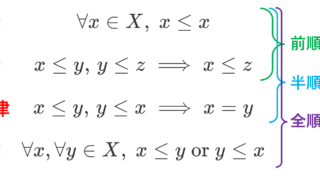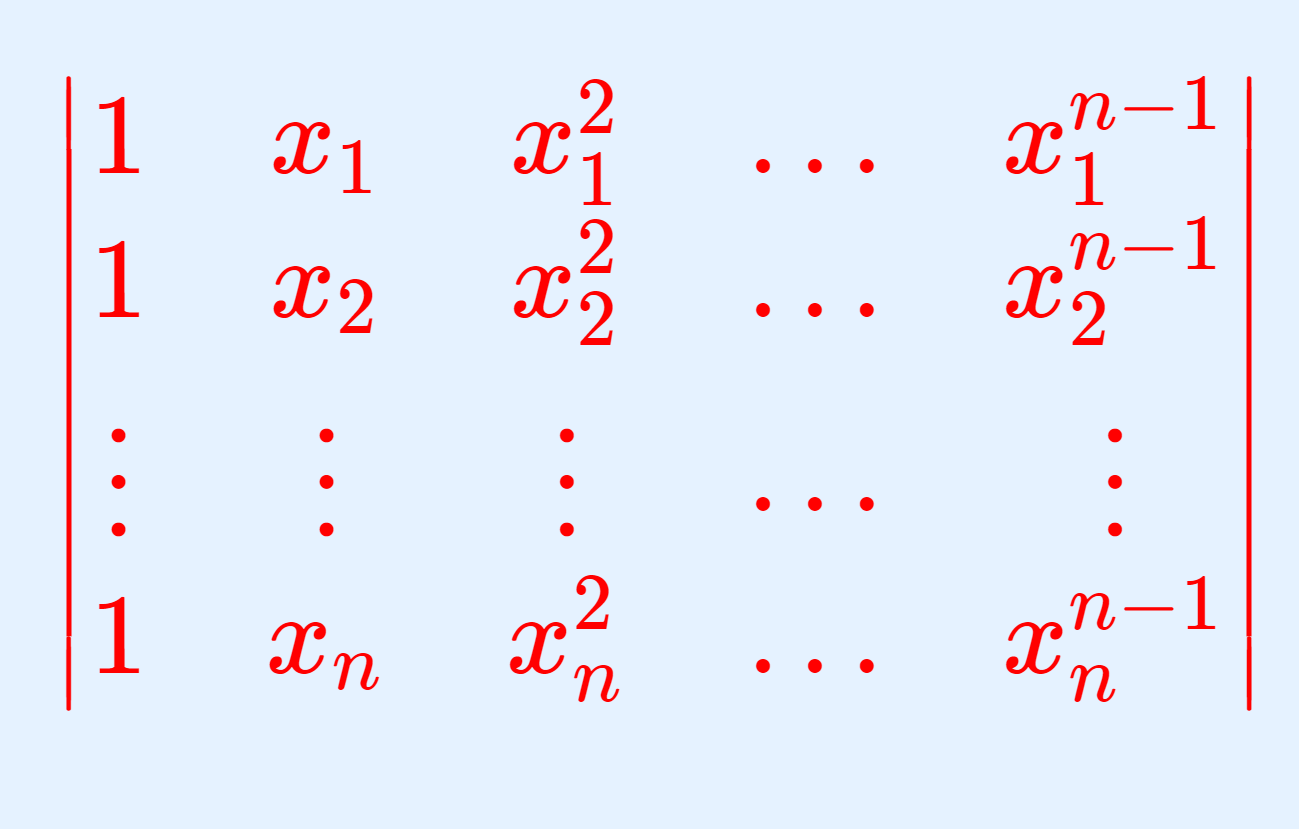実数の部分集合における上界・下界についてその定義と具体例を紹介します。
上界・下界・上に有界・下に有界の定義
定義(上界・下界・上に有界・下に有界)
A \subset \mathbb{R} を空でないとする。
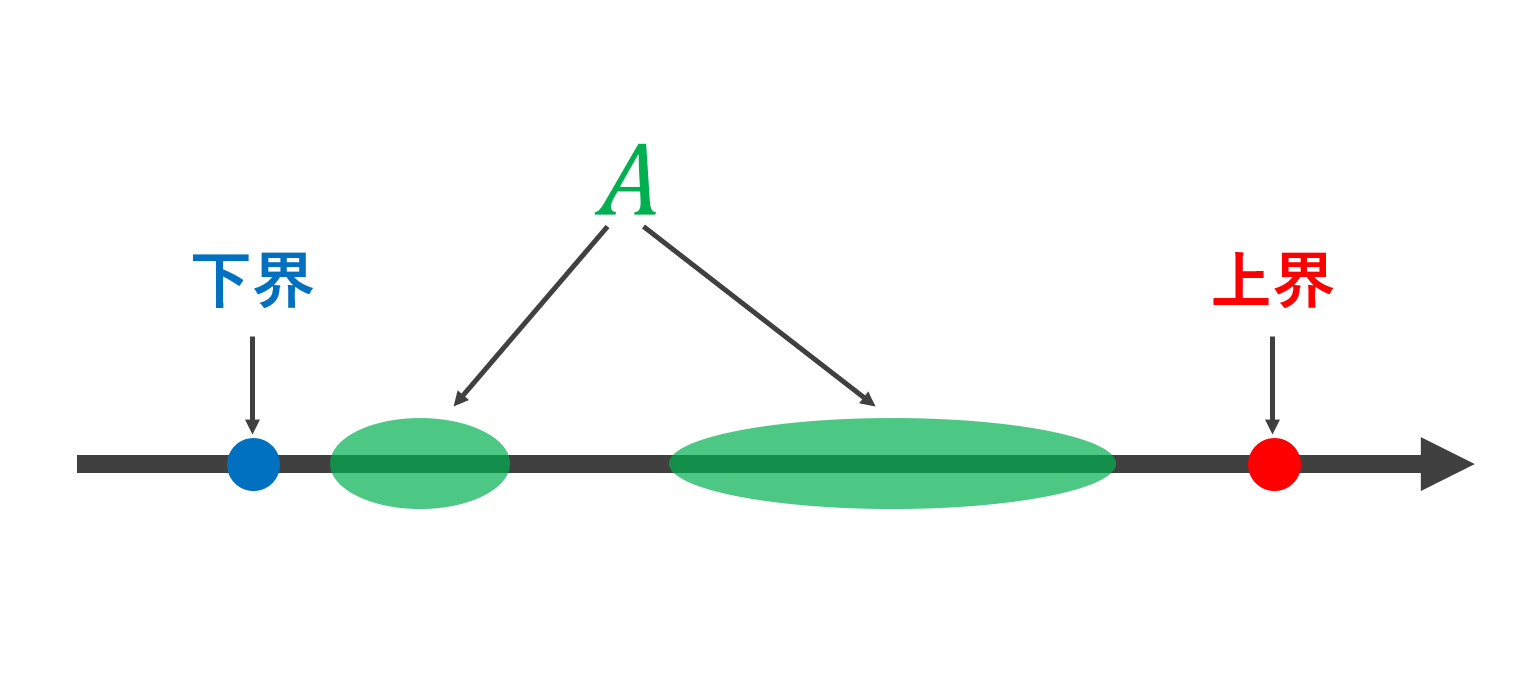
K \in \mathbb{R} が A の(一つの)上界 (upper bound) であるとは, \color{red} x \in A \implies x \le K が成立することであり,
L \in \mathbb{R} が A の(一つの)下界 (かかい; lower bound) であるとは, \color{red} x \in A \implies L \le x が成立することである。
上界が存在するとき, A は上に有界であるといい,下界が存在するするとき, A は下に有界であるという。
図で描くと次のような感じです。
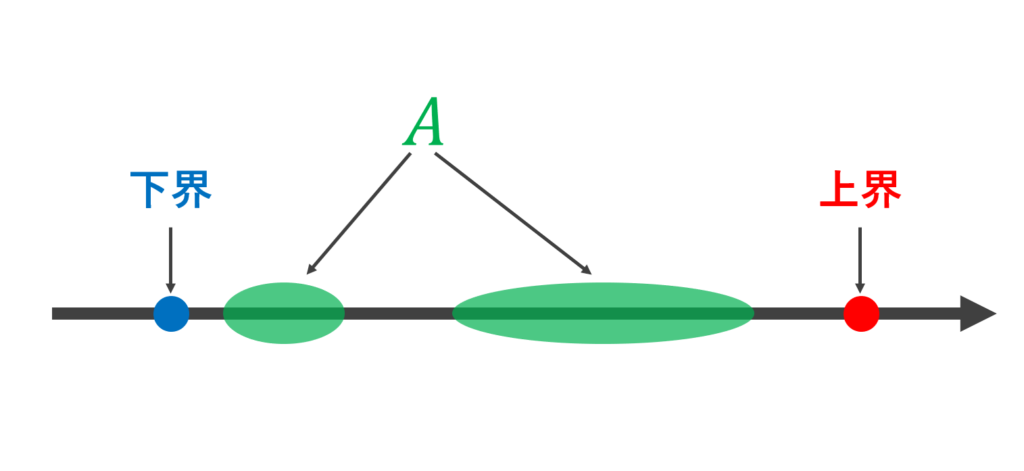
なお,今は実数 \mathbb{R} の部分集合を考えましたが,順序 \le が定義された集合(半順序集合)であれば何でも構いません。
A が上に有界かつ下に有界のとき, A は有界 (bounded) であるといいます。これについては,以下でも詳しく解説しています。
上界・下界の取り方は複数あり得ることに注意しましょう。実際,定義より直ちに次が成立します。
命題
K \in \mathbb{R} が A \subset \mathbb{R} の上界のとき, k \ge K となる任意の実数 k もまた A の上界である。
同様に, L \in \mathbb{R} が A \subset \mathbb{R} の下界のとき, l \le L となる任意の実数 l もまた A の下界である。
上界・下界の具体例
簡単かつ重要な具体例を挙げましょう。
上界・下界の具体例
- [0, 3] において, 3, 5, 2\pi は全て上界であり, 0, -3, -11/3 は全て下界である。
- (0, 3) において, 3, 5, 2\pi は全て上界であり, 0, -3, -11/3 は全て下界である。
- (0, \infty) の上界は存在しない。よって上に有界でない。
- \mathbb{Z} や \mathbb{Q} には上界・下界が存在しない。よって上にも下にも有界でない。
- A において最大値 M ,最小値 m が存在するとき, M, m はそれぞれ上界・下界である。特にそれぞれ上界のうち最小なもの,下界のうち最大のものになっている。
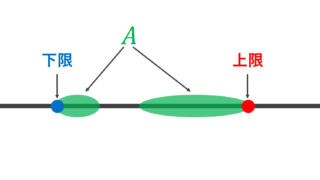
上限・下限
上界・下界のうち,最小・最大のものをそれぞれ上限・下限と言い,それぞれ \sup A, \inf A といった記号で表します。これは以下で詳しく解説していますから,そちらを参照してください。
より一般の順序集合における上界・下界
以下を参照してください。