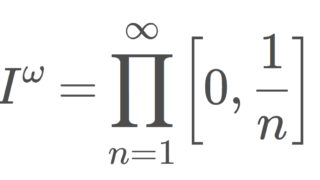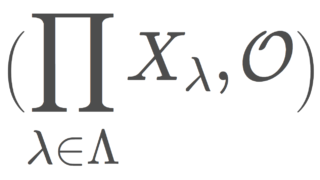ウリゾーンの距離化定理とは,位相空間が可分距離空間と思える必要十分条件を与える定理で,第二可算かつ正規ハウスドルフ空間(本サイトでは単に正規空間と言うだけでハウスドルフ性も含むとする)であることが必要十分です。
ウリゾーンの距離化定理について,その証明をしましょう。
ウリゾーンの距離化定理

本サイトでは,分離公理は一貫して次を採用しています。
| 名称 | 定義 |
|---|---|
| T_1 | 任意の異なる2点 x,y\in X に対して, x\in O_x,\, y\notin O_x となる開集合 O_x と x\notin O_y, \,y\in O_y となる開集合 O_y の両方が取れる |
| T_2 ハウスドルフ | 任意の異なる2点 x,y\in X が開集合で分離される, すなわち x\in O_x, \, y\in O_y,\, O_x\cap O_y=\emptyset となる開集合 O_x, O_y が取れる |
| T_3 | 任意の閉集合 F と任意の点 x\in X\setminus F が開集合で分離される, すなわち F\subset O_F,\, x\in O_x,\, O_F\cap O_x=\emptyset となる開集合 O_F, O_x が取れる |
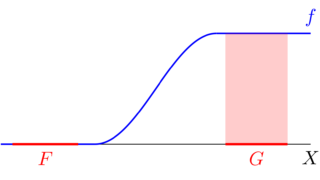
| T_4 | 任意の2つの互いに素な閉集合 F,G\subset X が開集合で分離される, すなわち F\subset O_F,\, G\subset O_G,\, O_F\cap O_G=\emptyset となる開集合 O_F, O_G が取れる |
| 正規 (normal) | T_1 かつ T_4( \iff T_2 かつ T_4\iff T_3 かつ T_4) |
注意ですが,文献によって, T_4 と正規の定義が逆のことがあります。いずれにせよ,今回のウリゾーンの距離化定理において正規空間とは,正規ハウスドルフ空間のことです。主張を見ていきましょう。
ウリゾーンの距離化定理 (Urysohn’s metrization theorem)
(X,\mathcal{O}) を位相空間とする。このとき,以下は同値である。
なお,第二可算のとき,正則空間 ( T_2 かつ T_3)と正規空間 ( T_2 かつ T_4) は同値なので,1.の「正規空間」は「正則空間」に置き換えてもかまいません。
証明
1. \implies 3.について
1.のとき,第二可算性から,\mathcal{B} を可算開基とする。
\mathcal{M}=\{ (U, V)\in\mathcal{B}\times \mathcal{B}\mid \overline{U}\subset V\}
と定めると, \mathcal{M} も可算集合なので, \mathcal{M}=\{(U_n, V_n)\} と番号付けしておく。 \overline{U_n}, \,X\setminus V_n は互いに素な閉集合であるから,ウリゾーンの補題より,
となる連続関数 f_n\colon X\to [0,1]=I が存在する。 f\colon X\to f(X)\subset I^\mathbb{N} を f(x)=\bigl(f_n(x)\bigr)_n\; (x\in X) と定める。これが同相写像であることを示せばよい。全射 であることは f\colon X\to f(X) で考えているので明らか。直積位相と普遍性より, f が連続であることも分かる。
f が単射であることを示そう。 x,y\in X,\; x\ne y とする。 X は T_1 なので, x\in V, y\notin V となる V\in \mathcal{B} が取れ,また T_1 かつ T_4 なら T_3 でもあるので, x\in U\subset \overline{U}\subset V となる U\in\mathcal{B} が取れる。このとき, (U, V)\in\mathcal{M} なので,ある n が存在して,(U,V)=(U_n, V_n) とかける。この n で f_n(x)=0\ne 1=f_n(y) であるから, f は単射である。
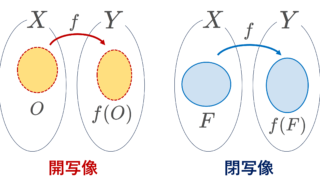
f が開写像であることを示そう。 O\subset X を開集合とする。 x\in O に対し, X は T_3 なので, x\in U\subset \overline{U}\subset O となる U\in\mathcal{B} が存在し,また X は T_4 なので, \overline{U}\subset V\subset \overline{V}\subset O となる V\in\mathcal{B} が存在する。 (U, V)\in\mathcal{M} なので,ある n が存在して,(U,V)=(U_n, V_n) とかける。 n で f_n(x)=0\ne 1=f_n(X\setminus O) であるから,
f_n(x)\notin \overline{f_n(X\setminus O)}
ゆえに,
ただし,最後の等号は直積位相とは~定義・具体例・性質~内で示した。 x\in O は任意であったから,
一方で,明らかに
なので,
である。右辺は f(X) における開集合であるから, f は開写像である。全単射・連続・開写像なら同相写像なので,証明が終わる。
3. \implies 2.について
x=(x_n), \, y=(y_n)\in I^\mathbb{N} に対し,
d(x,y) = \sum_{n=1}^\infty \frac{|x_n-y_n|}{2^n}
と定めると, I^\mathbb{N}=\prod_{n=1}^\infty [0,1] は距離空間である。また,可分な距離空間の部分空間は可分な距離空間であるから,2.が示せた(※ 関係ないが一般の位相空間では可分空間の部分空間が可分とは言えないことに注意)。
2. \implies 1.について
2.を仮定する。距離空間では,可分性と第二可算性は同値なので, X は第二可算であり,距離空間は正規なので,1.が成り立つ。
証明終
ヒルベルト立方体 I^\mathbb{N} については,以下で解説しています。