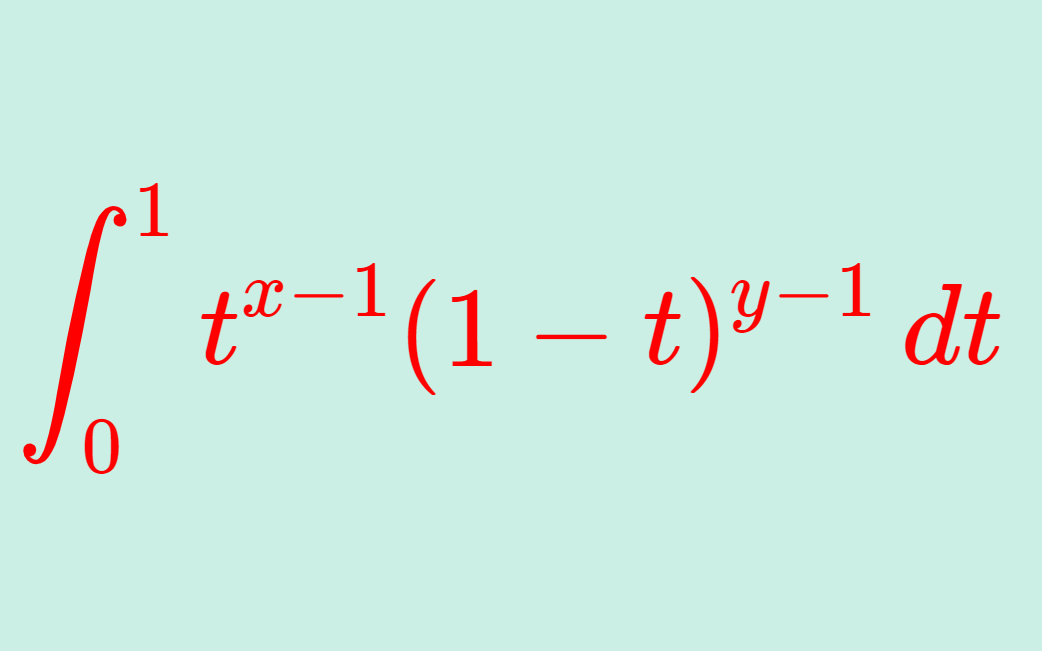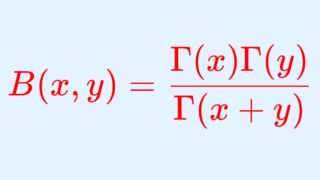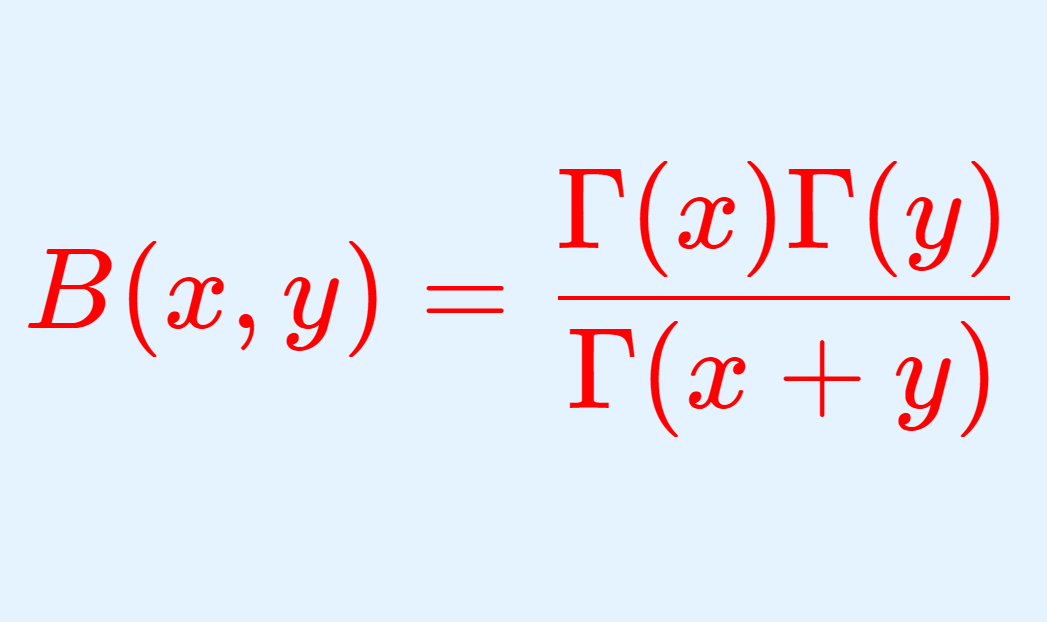ベータ関数とは, B(x,y) =\int_0^1 t^{x-1} (1-t)^{y-1}\, dt と定義される特殊関数です。これについて,その定義と性質とその証明を行いましょう。
ベータ関数の定義
\operatorname{Re} x, \,\operatorname{Re} y > 0 の複素数の範囲で定義しますが,複素関数が分からない場合は,単に x,y>0 と思って全く差し支えありません。
定義(ベータ関数)
\operatorname{Re} x, \,\operatorname{Re} y > 0 とする。
\color{red} B(x,y) = \int_0^1 t^{x-1} (1-t)^{y-1}\, dt
をベータ関数 (beta function) という。
ベータ関数の積分が収束することは, |t^z|= |e^{z\log t}| = e^{\operatorname{Re} (z)\log t} = t^{\operatorname{Re} z} に注意すると, \operatorname{Re} x - 1 >-1 ,\; \operatorname{Re} y-1>-1 であるから,
\small\begin{aligned}&\left|\int_0^1 t^{x-1} (1-t)^{y-1}\, dt\right| \\ &\le \int_0^1 |t^{x-1} (1-t)^{y-1}|\, dt \\ &\le \int_0^{1/2} \frac{1}{2^{\operatorname{Re}y-1}} t^{\operatorname{Re}x-1}\, dt + \int_{1/2}^1 \frac{1}{2^{\operatorname{Re}x-1}} (1-t)^{\operatorname{Re}y-1}\, dt \\ &\le \frac{1}{2^{\operatorname{Re}y-1}} \int_0^1 t^{\operatorname{Re}x-1}\, dt + \frac{1}{2^{\operatorname{Re}x-1}} \int_0^1 t^{\operatorname{Re}y-1}\, dt \\ &\le \frac{1}{2^{\operatorname{Re}y-1}\operatorname{Re}x} + \frac{1}{2^{\operatorname{Re}x-1}\operatorname{Re}y} <\infty \end{aligned}
となるため,分かりますね。
ベータ関数の性質8つ
定理(ベータ関数の性質)
\operatorname{Re} x, \,\operatorname{Re} y > 0 とする。このとき,
- B(x,y) = B(y,x).
- xB(x,y+1) = yB(x+1,y).
- B(x,y) = B(x+1,y) + B(x,y+1) .
- (x+y)B(x+1,y) = xB(x,y).
- (x+y)B(x,y+1) = yB(x,y).
- B(x,y) =\displaystyle 2\int_0^{\pi/2} \sin^{2x-1} \theta \cos^{2y-1}\theta\, d\theta.
- B(x,y) =\displaystyle \dfrac{1}{2^{x+y-1}}\int_{-1}^1 (1+t)^{x-1}(1-t)^{y-1}\, dt.
- B(1,x) = B(x,1) = \dfrac{1}{x}.
それぞれ証明していきましょう。
1. B(x,y) = B(y,x)
証明
u=1-t と置換積分すると,
\begin{aligned} B(x,y)&=\int_0^1 t^{x-1}(1-t)^{y-1}\, dt \\ &= \int_0^1 (1-u)^{x-1}u^{y-1}\, du \\ &= B(y,x). \end{aligned}証明終
2. xB(x,y+1) = yB(x+1,y)
証明
部分積分公式より,
\begin{aligned} &xB(x, y+1) \\ &= x\int_0^1 t^{x-1}(1-t)^{y}\, dt \\ &= \left[ t^x (1-t)^y \right]_0^1 + y \int_0^1 t^{x} (1-t)^{y-1}\, dt \\ &= y B(x+1,y). \end{aligned}証明終
3. B(x,y) = B(x+1,y) + B(x,y+1)
証明
ベータ関数の定義式より,
\begin{aligned}&B(x,y+1)\\ &= \int_0^1 t^{x-1}(1-t)^y \,dt \\ &= \int_0^1 t^{x-1}(1-t)^{y-1}(1-t) \,dt \\ &= \int_0^1 t^{x-1}(1-t)^{y-1} \,dt - \int_0^1 t^{x}(1-t)^{y-1}\,dt \\ &= B(x,y)-B(x+1,y) \end{aligned}
であるから,移項して B(x,y) = B(x,y+1)+B(x+1,y) .
証明終
4. (x+y)B(x+1,y) = xB(x,y)
証明
3.を適用してから2.を使うことで,
\begin{aligned} B(x,y) &= B(x,y+1)+B(x+1,y) \\ &= \frac{y}{x}B(x+1,y) + B(x+1,y) \\ &= \frac{x+y}{x} B(x+1,y). \end{aligned}
よって, (x+y)B(x+1,y) = xB(x,y) .
証明終
5. (x+y)B(x,y+1) = yB(x,y)
証明
3.を適用してから2.を使うことで,
\begin{aligned} B(x,y) &= B(x,y+1)+B(x+1,y) \\ &= B(x,y+1) +\frac{x}{y} B(x,y+1) \\ &= \frac{x+y}{y} B(x+1,y). \end{aligned}
よって, (x+y)B(x,y+1) = yB(x,y) .
証明終
6. B(x,y) = 2∫_0^{π/2} sin^{2x-1} Θ cos^{2y-1}Θ dΘ
証明
t=\sin^2 \theta とおくと, 1-t = \cos^2 \theta であり,
\begin{aligned} &B(x,y) \\ &= \int_0^1 t^{x-1}(1-t)^{y-1}\, dt \\ &= \int_0^{\pi/2} \sin^{2x-2}\theta \cos^{2y-2}\theta \,\, 2\sin\theta\cos\theta d\theta \\ &= 2\int_0^{\pi/2} \sin^{2x-1} \theta \cos^{2y-1}\theta\, d\theta. \end{aligned}証明終
7. B(x,y) = 1/2^{x+y-1}∫_{-1}^1 (1+t)^{x-1}(1-t)^{y-1} dt
証明
ベータ関数の定義式より,
B(x,y) = \int_0^1u^{x-1}(1-u)^{y-1}\, du.
t=2u-1 と置換積分すると,
証明終
8. B(1,x) = B(x,1) = 1/x
証明
前半の等式は1.からわかる。後半の等式については,ベータ関数の定義より,
\begin{aligned} B(x,1) &= \int_0^1 t^{x-1}\, dt = \left[\frac{t^x}{x}\right]_0^1 = \frac{1}{x}\end{aligned}
よりわかる。
証明終
ベータ関数とガンマ関数の関係
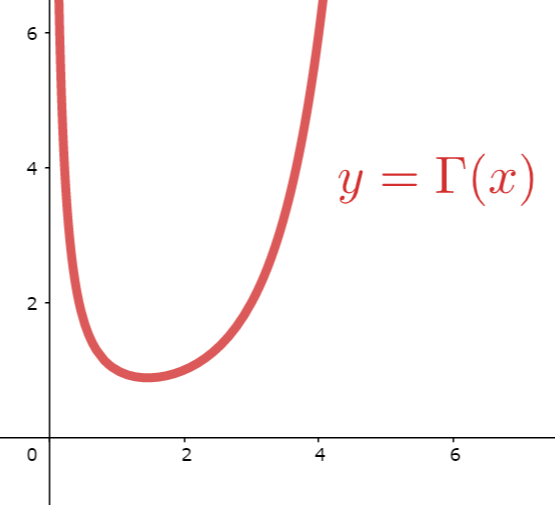
\Gamma(z) = \int_0^\infty t^{z-1}e^{-t}\, dt \quad (\operatorname{Re}z>0)
をガンマ関数としましょう(→ ガンマ関数とは~定義と性質をわかりやすく~)。このとき,ベータ関数とガンマ関数の間には,以下の関係があります。
これは,以下で解説しています。
これを踏まえると,ガンマ関数の値を用いることで,
等も分かります。