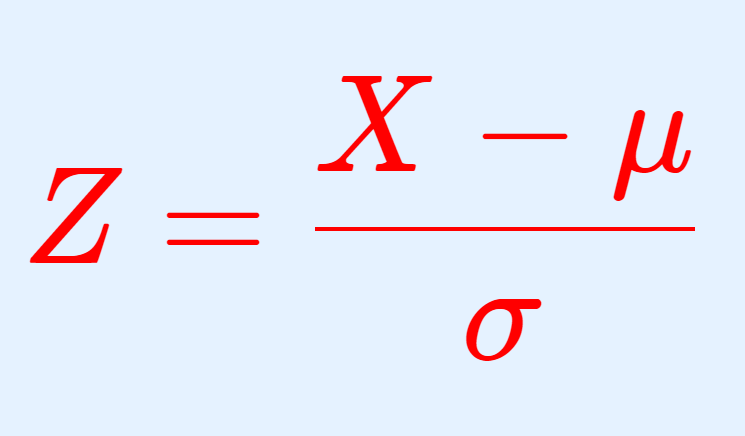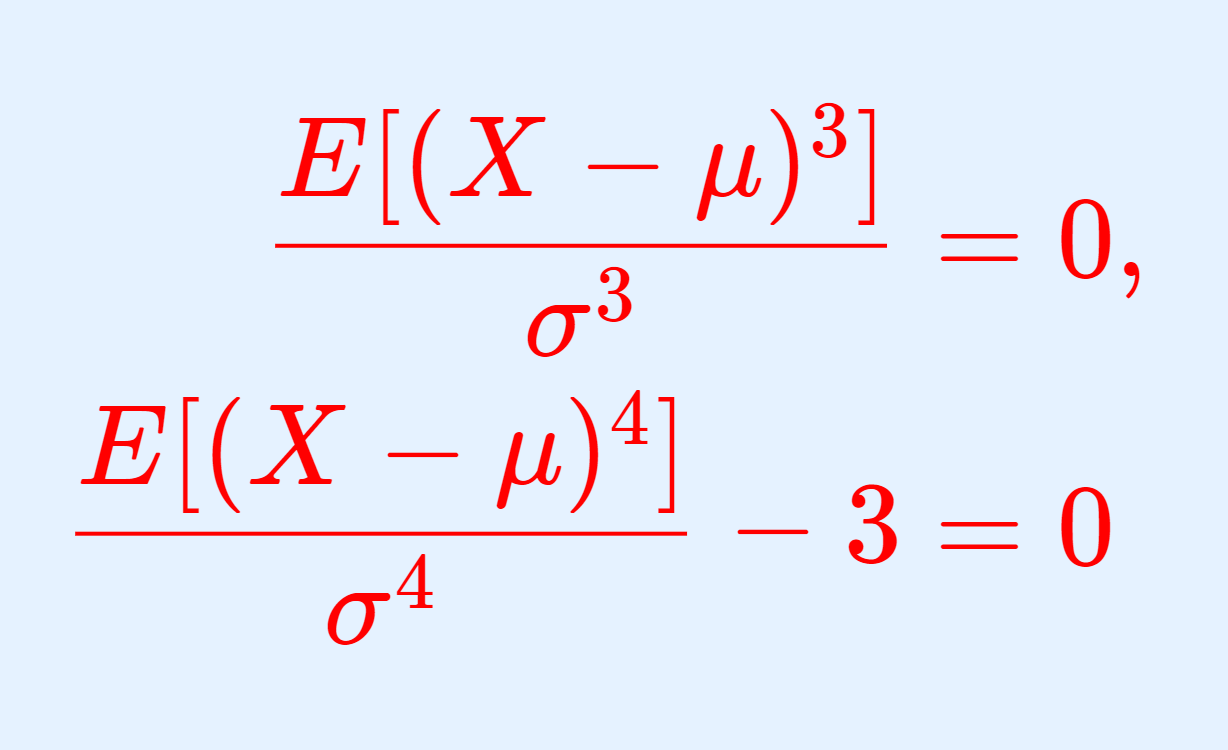正規分布の標準化とその証明

$X\sim N(\mu, \sigma^2)$ のとき， $Z = \dfrac{X-\mu}{\sigma}$ とスケール変換すると， $Z\sim N(0,1)$ になります。これを，正規分布の標準化といいます。これについて詳しく述べ，証明しましょう。

正規分布の標準化

定理（正規分布の標準化）

$X\sim N(\mu, \sigma^2)$ とするとき，

\large\color{red} Z = \frac{X-\mu}{\sigma}

とすると， $Z\sim N(0,1)$ になる。

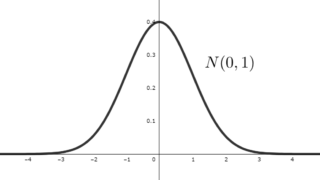
正規分布の標準化 (standardization) とは， $N(\mu,\sigma^2)$ （平均 $\mu$ ，分散 $\sigma^2$ の正規分布）に従う確率変数を，変換によって $N(0,1)$ （平均 $0$ ，分散 $1$ の標準正規分布）に従うようにすることです。

正規分布を標準化すれば，標準正規分布表を利用することができますから，統計学においては，何かと便利です。

なお一般に， $E[aX+b] = aE[X]+b, \; V(aX+b) = a^2 V(X)$ ですから，

\begin{aligned}& E[X] =\mu, \quad V(X) = \sigma^2 \\ &\implies E[Z] = 0,\quad V(Z) = 1\end{aligned}

となることは明らかです。ここで大切なのは，単に $Z$ の期待値・分散が $0, 1$ になることではなく， $Z$ がちゃんと再び正規分布に従うことです。

これについて，証明してみましょう．

正規分布 $N(\mu, \sigma^2 )$ の確率密度関数 $p(x)$ は

p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}

となることを思い出しましょう。

証明

$a<b$ に対し， $P(a\le Z\le b)$ を考える。 $X\sim N(\mu,\sigma^2)$ であるから，

\begin{aligned} P(a\le Z\le b) &= P(a\le \frac{X-\mu}{\sigma}\le b) \\ &= P(\mu+\sigma a \le X \le \mu+\sigma b) \\ &= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{\mu+\sigma a}^{\mu+\sigma b} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx. \end{aligned}

ここで， $z = \dfrac{x-\mu}{\sigma}$ とおいて置換積分すると，

\begin{aligned} &\frac{1}{\sqrt{2\pi\sigma^2}}\int_{\mu+\sigma a}^{\mu+\sigma b} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \, dx \\ &= \frac{1}{\sqrt{2\pi\sigma^2}}\int_{a}^{b} e^{-\frac{z^2}{2}} \, \sigma dz \\ &= \frac{1}{\sqrt{2\pi}}\int_{a}^{b} e^{-\frac{z^2}{2}} \, dz \end{aligned}

であるから， $Z$ の確率密度関数は $\frac{1}{\sqrt{2\pi}}e^{-\frac{z^2}{2}}$ となる。これは， $Z\sim N(0,1)$ を意味する。

証明終