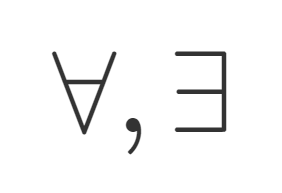
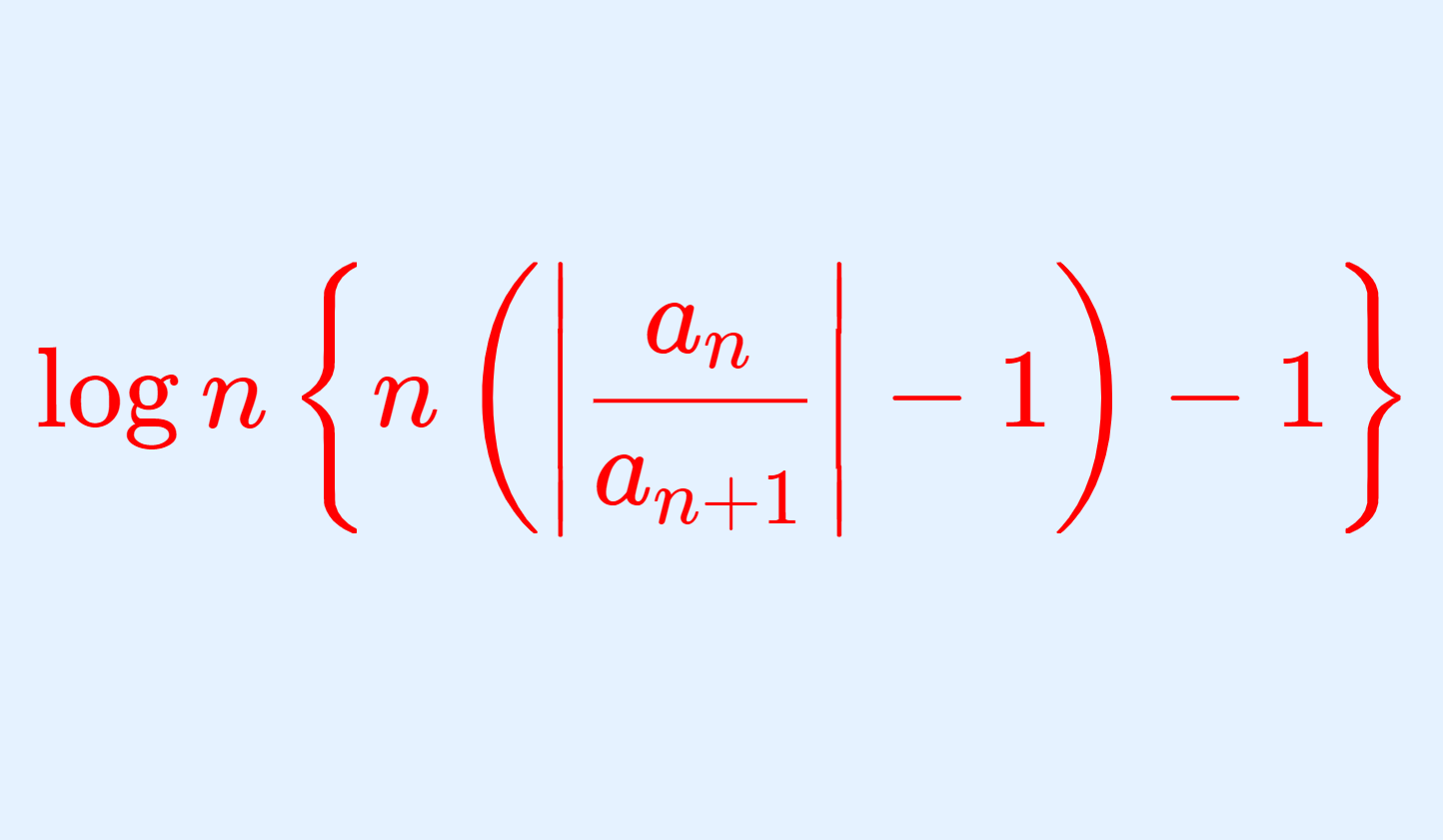大学数学において,授業やセミナー,ときどき論文や教科書でも使われる記号である,∀(任意の)と∃(存在する)は,それぞれ「全称記号」「存在記号」といわれます。たとえば,
\forall x> 0,\; x^2>0.
は,「任意の x>0 に対して, x^2>0 が成立する」と同じ意味です。
これについて,その定義・使い方を,さまざまな具体例を交えて解説します。
∀(全称記号,任意の)と∃(存在記号,存在する)の定義
定義( \forall, \exists )
「任意の~に対して」「全ての~に対して」を記号 \forall を用いて, \color{red}\boldsymbol{\forall \sim } とかくことがある。これを全称記号という。
「ある~が存在して」「少なくとも一つ~があって」を記号 \exists を用いて, \color{red}\boldsymbol{ \exists \sim} とかくことがある。これを存在記号という。
\forall は「任意・全て」を表す All の “A” をひっくり返したもの, \exists は「存在」を表す Exists の “E” をひっくり返したものです。
ちなみに, \LaTeX においてこれを出力するには, \forall は \forall, \exists は \exists とかきます(→【LaTeX】論理記号(否定,かつ,または,任意,存在など)一覧)。
なお,本サイトの他の記事においては,基本的にこの記号は用いずに解説しています。
∀(全称記号,任意の)と∃(存在記号,存在する)の使い方の例
定義を眺めるより,具体例を確認した方が手っ取り早いので,そうしましょう。
例1.
以下の2つは同じ意味である。(ただし, \mathbb{R} は実数全体の集合を指す)
- 任意の x\in \mathbb{R} に対して, x^2 \ge 0 が成立する。
- \forall x\in\mathbb{R} , \; x^2\ge 0.
「任意の~」の部分が \forall に置き換わっており,コンマで区切って,後ろの主張が書かれていますね。なお,コンマで区切る代わりに,
- \forall x\in \mathbb{R};\; x^2 \ge 0.
- \forall x\in\mathbb{R} \; [x^2\ge 0].
- \forall x\in\mathbb{R} \,\text{ s.t. }\, x^2\ge 0.
のようなかき方をすることもあります。s.t. は such that の略で,「…のような」くらいの意味です。数学では,後ろに主張を書きたいときに,これを用いることがあります。
例2.
以下の2つは同じ意味である。
- ある x\in\mathbb{R} が存在して,x^2 = 0 が成立する。
- \exists x\in\mathbb{R},\; x^2=0.
なお「ある~が存在して…」というのは,「…となる~が存在する」と同じ意味です。英語では,”There exists ~ such that …” という言い方をするため,その語順に合わせて日本語訳されることが多いです。いつも英語で読み書きしている研究者にとっては,その方が都合がいい訳ですね。
先ほどの例と同じく,[] で囲ったり,s.t. を用いて書かれることもあります。
例3.
次の2つは同じ意味である。
- 任意の x\in \mathbb{R} に対して,ある y\in\mathbb{R} が存在して, x+y=0 とできる。
- \forall x\in \mathbb{R}, \exists y\in \mathbb{R},\; x+y=0.
このように,論理記号を複数並べて書くことも可能です。
ここで, y の取り方は, x によって変えても構いません。実際,上の場合は y=-x ですね。 y の取り方は, x に依存して良いわけです。
例4.
次の2つは同じ意味である。
- ある y\in \mathbb{R} が存在して,任意の x\in \mathbb{R} に対して, xy=0 とできる。
- \exists y\in \mathbb{R}, \forall x\in \mathbb{R},\; xy=0.
さっきと, \forall, \exists の順番が逆なことに注意しましょう。
このとき,例3とは違って, y は x に依存してはいけません。「どんな x でも成立する」ような y を取れると言っているからです。
今回の主張の場合は, y=0 と取れば,全ての x で xy=0 が成立しますね。
例5(イプシロンエヌ論法).
以下の2つは同じ意味である。
- 任意の \varepsilon >0 に対して,ある N\ge 0 が存在して, n\ge N \implies |a_n-a| < \varepsilon が成立する。
- \forall \varepsilon > 0, \exists N \ge 0, \; n\ge N \implies |a_n-a| < \varepsilon.
これは,大学で最初で習うイプシロンエヌ論法の主張です。イプシロンエヌ論法については,イプシロンエヌ論法をわかりやすく丁寧に~数列の極限の定義~を参照してください。
「ただ一つ存在」の記号∃!, ∃1
存在するの記号 \exists において,その存在がただ一つであるときは,
\color{red}\large \exists ! ,\quad \exists 1
などの記号を用います。たとえば,以下の2つは同じ意味です。
- 任意の x>0 に対して, xy=1 となる y>0 がただ一つ存在する。
- \forall x>0, \exists ! \,y>0, \; xy=1.
これらの記号は,大学数学の授業やセミナーで多く目にすることになるでしょう。しっかりと理解しておきたいところです。