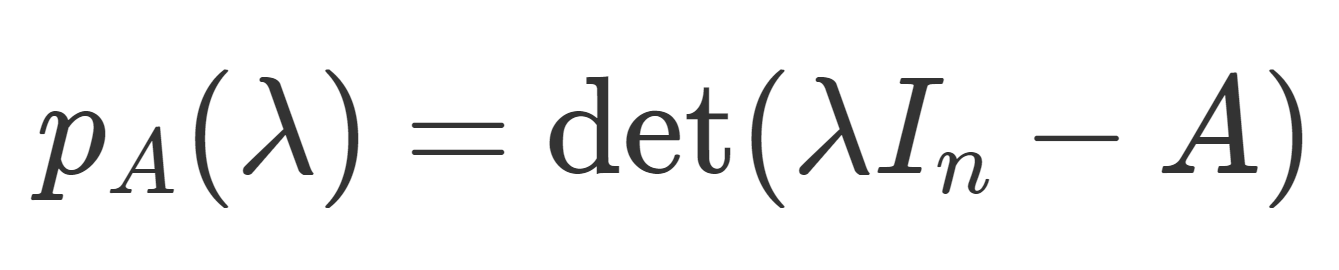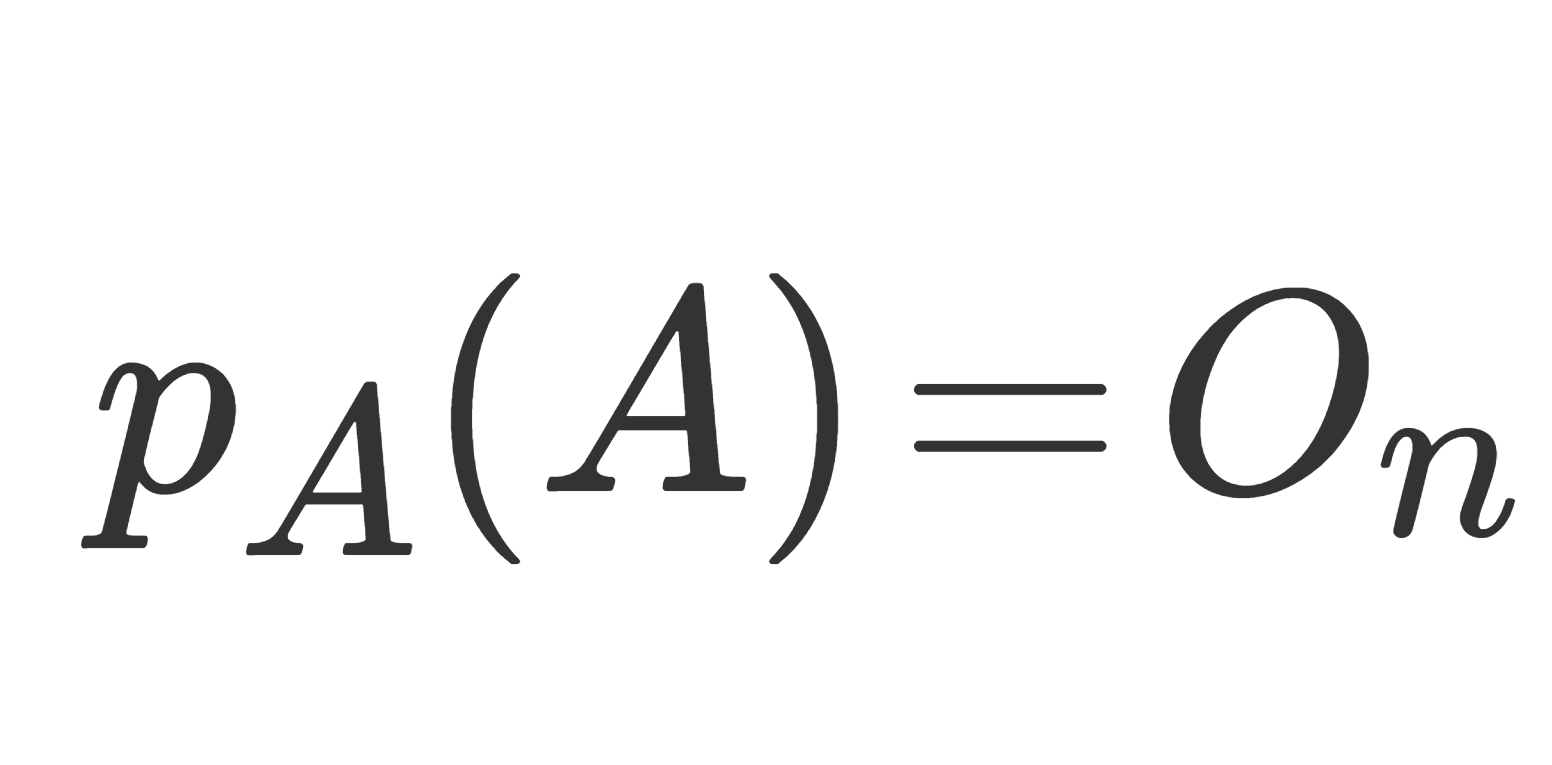正方行列における,固有多項式・最小多項式について,その定義と求め方,性質を順番に解説していきましょう。
固有多項式の定義と求め方
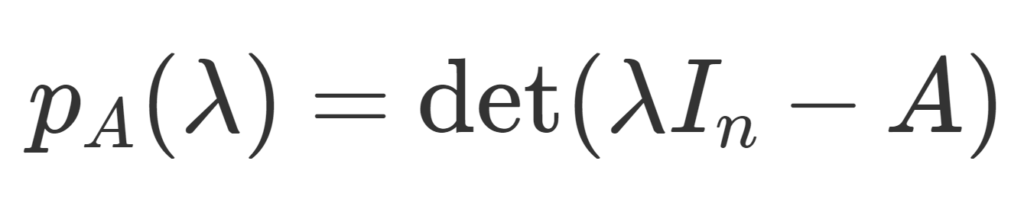
固有多項式の定義
定義(固有多項式)
A を n 次正方行列とする。このとき,
\color{red}\large p_A(\lambda)=\det (\lambda I_n-A)
を固有多項式 (characteristic polynomial) という。I_n は n 次単位行列である。
行列式の定義を考えることで, p_A(\lambda) は最高次が \lambda^n となる多項式になっていることが分かるでしょう。
なお, p_A(\lambda)=0 の解 \lambda\in\mathbb{C} を固有値 (eigenvalue) といいます。
固有多項式の求め方
固有多項式を求めるには,行列式 \det (\lambda I_n -A) の計算をすればよいです。これについては,固有値の求め方の途中で現れるため,以下が参考になると思います。
あるいは,行列式の求め方の記事を見るといいでしょう。
最小多項式の定義と求め方
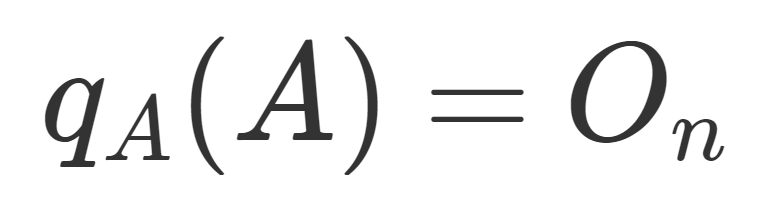
最小多項式の定義
定義(最小多項式)
A を n 次正方行列とする。最高次係数が 1 の多項式 q_A(\lambda) のうち,
\large \color{red} q_A(A)=O_n
となるもので次数が最小のものを A の最小多項式 (minimal polynomial) という。 O_n は n 次零行列である。
行列を代入して零行列になる,最小次数の多項式を最小多項式というわけですね。
ここで,多項式 f(x)=a_nx^n +a_{n-1}x^{n-1}+\dots + a_0 に対し,
f(A)=a_n A^n +a_{n-1} A^{n-1}+\dots + a_0 I_n
と考えます。
最小多項式の求め方
最小多項式を求めるには,以下の性質を用います。
- 固有多項式は最小多項式で割り切れる(次々節性質1.)
- 最小多項式は全ての固有値を根にもつ(次々節性質3.)
性質の証明は,あとに「固有多項式・最小多項式の性質」のところで行います。
上を参考に,以下の手順で求めましょう。
- 固有多項式 p_A(\lambda) を求める。 p_A(\lambda)=(\lambda-\lambda_1)^{a_1} \dots (\lambda-\lambda_n)^{a_n} とする。
- (\lambda-\lambda_1)^{i_1} \dots (\lambda-\lambda_n)^{i_n}\;(1\le i_1\le a_1,\dots, 1\le i_n\le a_n) に A を代入して実際に O_n になるものを見つける。
次節で具体例を挙げます。
固有多項式・最小多項式の例
例1.
A=\begin{pmatrix} 1 &0&0\\ 0&2&0\\ 0&0&2\end{pmatrix} とすると,
固有多項式は \color{red}p_A(\lambda)= (\lambda-1)(\lambda-2)^2 で,最小多項式は \color{red} q_A(\lambda)=(\lambda-1)(\lambda-2) である。
固有多項式は
\begin{aligned} p_A(\lambda)&=\det (\lambda I_3-A)\\&= \begin{vmatrix}\lambda-1 & 0 & 0\\ 0& \lambda-2 & 0 \\ 0&0&\lambda-2 \end{vmatrix}\\&= (\lambda-1)(\lambda-2)^2\end{aligned}
です。これより,最小多項式は (\lambda-1)(\lambda-2) か (\lambda-1)(\lambda-2)^2 のどちらかです。ここで,
ですから,最小多項式は q_A(\lambda)= (\lambda-1)(\lambda-2) とわかります。(ここで, (A-1)(A-2) は厳密には (A-I_3)(A-2I_3) です)
例2.
B=\begin{pmatrix} 1 &2&-1\\ 0&1&0\\ 0&0&1\end{pmatrix} とすると,
固有多項式は \color{red}p_B(\lambda)= (\lambda-1)^3 で,最小多項式は \color{red} q_B(\lambda)=(\lambda-1)^2 である。
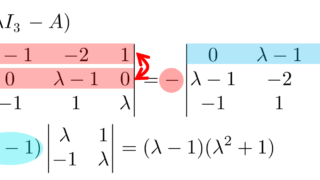
固有多項式は
\begin{aligned} p_A(\lambda)&=\det (\lambda I_3-B)\\&= \begin{vmatrix}\lambda-1 & -2 & 1\\ 0& \lambda-1 & 0 \\ 0&0&\lambda-1 \end{vmatrix}\\&= (\lambda-1)^3\end{aligned}
であり,
ですから,最小多項式は q_A(\lambda)=(\lambda-1)^2 です。
固有多項式・最小多項式の性質
以下はどれも押さえておくべき性質です。
定理(固有多項式・最小多項式の性質)
- 正方行列 A の固有多項式 p_A(\lambda) は最小多項式 q_A(\lambda) で割り切れる。
- 正方行列 A,B が相似であるとするとき,A,B の最小多項式は一致する。すなわち, q_A(\lambda)=q_B(\lambda) である。
- 最小多項式は固有値を根にもつ。すなわち, A の最小多項式 q_A(\lambda) について, \alpha\in\mathbb{C} を A の固有値とすると, q_A(\alpha)=0 となる。
A,B が相似とは,ある正則行列(可逆行列) P が存在して, B=P^{-1}AP とできることを言います(→行列の相似とは~定義と性質6つの証明~)。
どれも重要な性質ですから,順番に証明していきましょう。
1. 固有多項式p_A(λ)は最小多項式q_A(λ)で割り切れる
ケーリーハミルトンの定理より, p_A(A)=O であることを用います(→ケーリーハミルトンの定理とその厳密な証明をわかりやすく)。
証明
p_A(\lambda) を q_A(\lambda) で割った商を s(\lambda),余りを r(\lambda) とする。すなわち,
p_A(\lambda)=q_A(\lambda)s(\lambda)+r(\lambda)
とする。ケーリーハミルトンの定理より, p_A(A)=O なので,両辺に A を代入すると r(A)=O となる。 r(\lambda)=0 でないと, q_A が最小多項式であることに矛盾するので, r(\lambda)=0 であり,
なので p_A(\lambda) は q_A(\lambda) で割り切れる。
証明終
この定理より, n 次正方行列の最小多項式の次数は n 以下であることが分かります。
2. 相似ならば固有多項式・最小多項式は等しい
以下で n 次正方行列 A,B は相似,すなわち P を正則行列(可逆行列)として B=P^{-1}AP としましょう。
証明
固有多項式が等しいこと
\begin{aligned} p_B(\lambda)&= \det (\lambda I_n-B)\\ &= \det ( \lambda I_n-P^{-1}AP) \\ &= \det (P^{-1} (\lambda I_n-A ) P) \\ &= (\det P)^{-1} \det (\lambda I_n -A) \det P \\ &= \det (\lambda I_n -A) \\ &= p_A(\lambda). \end{aligned}
途中で行列式の積の性質を用いた(→行列式の性質6つの証明(列,行の線形性,置換,積,転置など))。
最小多項式が等しいこと
q_A(\lambda) を A の最小多項式とする。このとき,
q_A(B)= q_A( P^{-1}AP )=P^{-1} q_A(A) P = O_n
より, q_A に B を代入しても零行列になる。したがって, q_B を B の最小多項式とすると, q_B の次数は q_A 以下である。同様に q_A の次数は q_B 以下である。したがって, q_A=q_B である。
証明終
3. 最小多項式は固有値を根にもつ
証明
A を n 次正方行列, q_A(\lambda) をその最小多項式とする。
さらに \alpha \in\mathbb{C} を固有値, \boldsymbol{x} をそれに対応する固有ベクトルとする。このとき, A^m \boldsymbol{x}=\alpha A^{m-1}\boldsymbol{x}=\dots =\alpha^m \boldsymbol{x} である。これより,
\boldsymbol{0}=O_n \boldsymbol{x} =q_A(A)\boldsymbol{x}=q_A(\alpha)\boldsymbol{x}
なので, q_A(\alpha)=0 である。よって q_A(\lambda)=0 は固有値 \alpha を解に持つ。
証明終
無事にすべて証明できましたね。