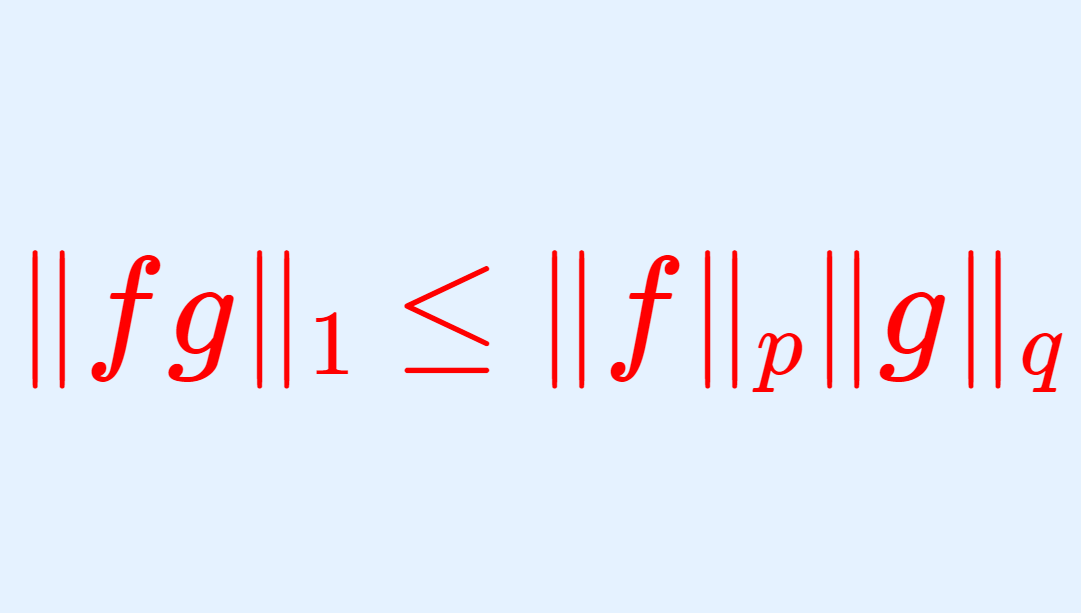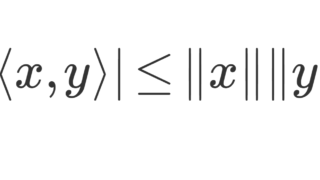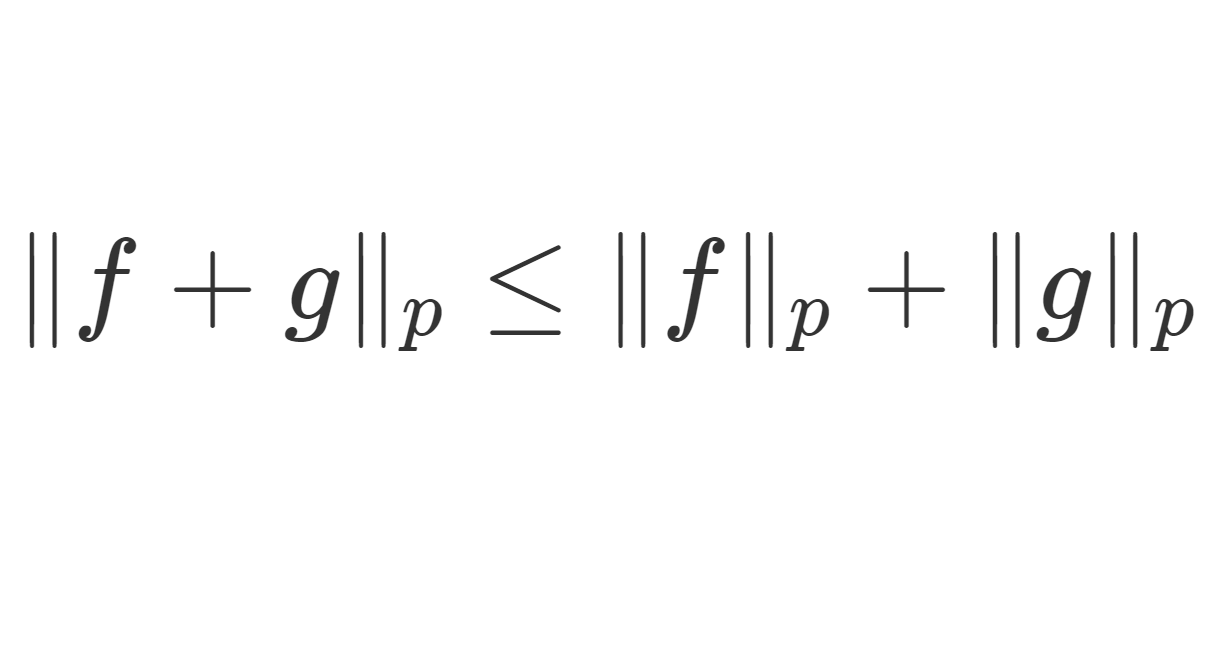ヘルダーの不等式とは,関数解析学における基本的な不等式であり,コーシーシュワルツの不等式の一般化にもなっています。
ヘルダーの不等式について,その主張と証明を分かりやすく紹介します。
ヘルダーの不等式
ヘルダーの不等式 (Hölder’s inequality)
1\le p,q\le \infty,\; 1/p+1/q=1 であり, f\in L^p(\mathbb{R}),\; g\in L^q(\R) とする ( p=\infty なら q=1 とする。逆も同じ)。このとき,
\color{red}\large \| fg\|_1 \le \| f\|_p \|g\|_q
である。 \|\cdot \|_p は L^p ノルムを意味する。すなわち, 1<p,q<\infty のときは
が成り立つ。特に fg\in L^1(\R) である。
これはコーシーシュワルツの不等式の一般化になっています。実際, p=q=2 とすると,
\int_\R |fg|\,dx\le \sqrt{\int_\R |f|^2\,dx} \sqrt{\int_\R |g|^2\,dx}
であり,すなわち |\langle f,g\rangle|\le \| f\|_2 \|g\|_2 となりますね。
また,ヘルダーの不等式は一般の測度空間上の積分でも証明可能です(証明はこれから紹介するものと全く同じです)。すなわち, 1<p,q<\infty のときは
\int |fg|\,d\mu\le \left(\int_\R |f|^p\,d\mu\right)^{1/p} \left(\int_\R |g|^q\,d\mu\right)^{1/q}
です。\mu =\sum_{n=1}^\infty {\delta_n} ( \delta_n は n に重みを持つデルタ測度) とすれば,級数版のヘルダーの不等式
も導けます。
ヘルダーの不等式の証明
証明すべきは 1/p+1/q=1 に対し, \| fg\|_1 \le \| f\|_p \|g\|_q であり,特に 1<p,q<\infty のときは
\int_\R |fg|\,dx\le \left(\int_\R |f|^p\,dx\right)^{1/p} \left(\int_\R |g|^q\,dx\right)^{1/q}
でした。早速証明をやっていきましょう。
証明
1<p,q<\infty のとき
\|f\|_p=0 のとき, f=0,\; \text{a.e.} なので, fg=0,\; \text{a.e.} であり, \|fg\|_1=0 より明らか。 \|g\|_q=0 でも同じなので, \|f\|_p, \|g\|_q>0 としてよい。
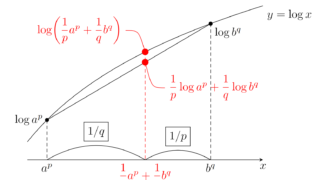
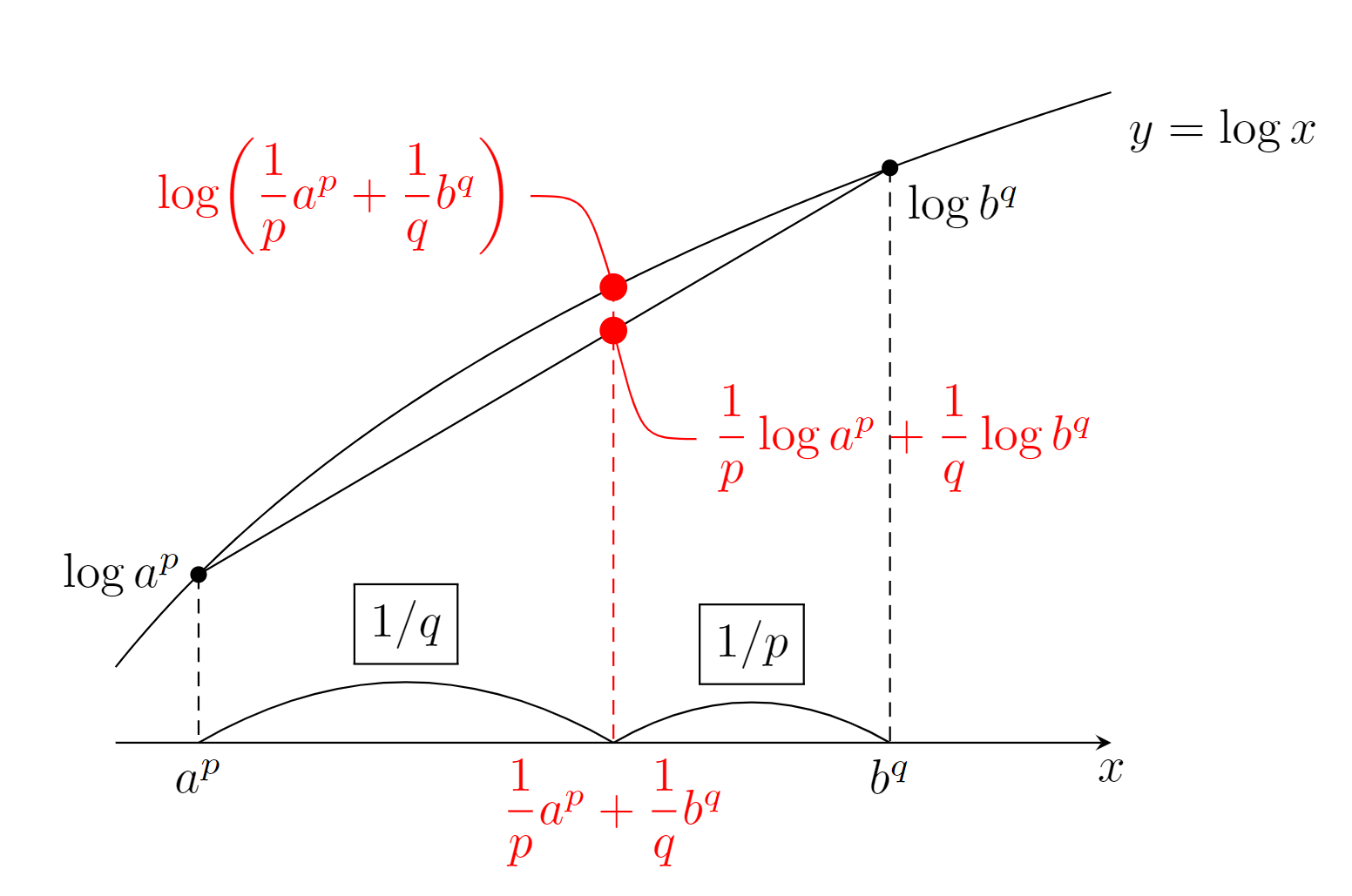
\tilde{f}=f/\|f\|_p,\; \tilde{g}=g/\|g\|_q とする。このとき, \|\tilde{f}\|_p = \|\tilde{g}\|_q=1 である。ヤングの不等式より,
|\tilde{f}\tilde{g}|\le \frac{|\tilde{f}|^p}{p}+\frac{|\tilde{g}|^q}{q}
である(→ヤングの不等式の証明とその一般化)。この両辺積分すると,
なので,
である。よって \| fg\|_1 \le \| f\|_p \|g\|_q である。
p=\infty または q=\infty のとき
同じことなので, p=\infty, \; q=1 とする。 |f|\le \|f\|_\infty,\;\text{a.e.} なので,
\begin{aligned}\int_\R |fg|\,dx &\le \int_\R \|f\|_\infty |g|\,dx \\ &= \|f\|_\infty\int_\R |g|\,dx \end{aligned}
すなわち, \|fg\|_1\le \|f\|_\infty \|g\|_1 である。
証明終
なお, 1<p,q<\infty のとき,等号成立は f=0,\;\text{a.e.} または g=0,\;\text{a.e.} または |{f}|^p = c|{g}|^q \; \text{a.e.} となる定数 c が存在するときになります。これは,ヤングの不等式の等号成立条件を考えればわかります。
p=\infty のときの等号成立条件は g=0,\;\text{a.e.} または |f| がa.e.で定数関数であることです。