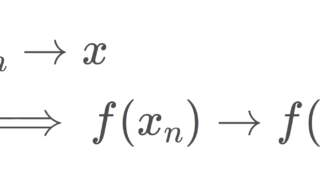第一可算公理と第一可算な位相空間の性質・具体例

第一可算とは，各点が高々可算な基本近傍系をもつ位相空間，すなわち可算個の近傍で各点周りの開集合が記述できるような空間です。第一可算な空間は，点列の収束で多くの性質が記述できる良い性質をもちます。

第一可算について，その定義と点列で扱えるという性質，それから具体例を紹介しましょう。

第一可算公理とは
第一可算な位相空間の性質
第一可算な空間やそうでない空間の具体例
関連する概念
関連する記事
参考

第一可算公理とは

定義（第一可算）

$(X,\mathcal{O})$ を位相空間とする。各 $x\in X$ が高々可算個からなる基本近傍系をもつとき， $X$ は第一可算 (first countable) または第一可算公理をみたす (first axiom of countability) という。

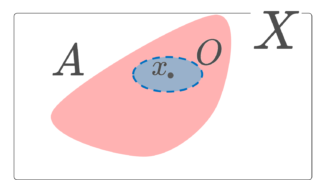
基本近傍系の定義を復習しておきましょう。 $x\in X$ の近傍 (neighborhood) とは， $x\in \operatorname{Int}(A)$ となる部分集合 $A\subset X$ のことを指します。ただし， $\operatorname{Int}(A)$ とは， $A$ の内部(開核)を意味します。

基本近傍系の定義

$(X, \mathcal{O})$ を位相空間とし， $x\in X$ に対し， $\mathcal{N}(x)$ を $x$ の近傍系(近傍全体の集合)とする。

$\mathcal{B}(x)\subset \mathcal{N}(x)$ が $x$ の基本近傍系 (neighbourhood basis) であるとは，任意の $N\in \mathcal{N}(x)$ に対し，ある $B\in \mathcal{B}(x)$ が存在して， $x\in B\subset N$ とできることをいう。

基本近傍系とは，どんなに小さな近傍を取ってきても，その近傍に含まれる集合が基本近傍系の中から取ってこれるような集合族です。

基本近傍系のイメージについては，以下の記事の後半で膨らませておいてください。

第一可算な位相空間の性質

第一可算な位相空間は，点列でさまざまな性質を記述できる便利な空間です。

距離空間は常に第一可算
集積点と部分収束列の存在
閉集合と点列の存在
開集合・閉集合の点列の特徴づけ
連続写像の点列の特徴づけ
第一可算な位相空間の直積

の順番に紹介しますが，1.から5.は「第一可算な空間は点列で記述できる」という話です。

1. 距離空間は常に第一可算

距離空間は，第一可算公理をみたす典型例です。イメージを膨らませましょう。

定理1（距離空間は常に第一可算）

距離空間 $(X, d)$ は第一可算である。

証明

$x\in X,\, \varepsilon >0$ に対し， $\varepsilon$ -近傍を

B_\varepsilon (x)= \{ y\in X\mid d(x,y)<\varepsilon\}

と定めると， $\{ B_{1/n} (x)\}_{n=1}^\infty$ は $x$ の可算な基本近傍系である。よって，第一可算である。

証明終

位相空間は距離空間の一般化ですが，第一可算でない位相空間は，位相空間独特なものです。

2. 集積点と収束部分列の存在

定理2（集積点と収束部分列の存在）

$(X,\mathcal{O})$ を第一可算な位相空間とする。このとき，次の2つは同値である。

$x\in X$ が点列 $(x_n)$ の集積点である
$(x_n)$ の部分列で， $x$ に収束するものが存在する

なお，第一可算でないと2. $\implies$ 1.しか言えない。後の例6.で紹介する。

$x$ が点列 $(x_n)$ の集積点 (accumulation point) であるとは， $x$ の任意の開近傍 $U\subset X$ と任意の $N\ge 1$ に対し， $x_n \in U$ となる $n\ge N$ が存在することを言います。これを， $(x_n)$ is frequently in $U$ ということがあります。よって， $y, x, x, x, \ldots$ みたいなときの $x$ も集積点に含みます。

また，点列 $(x_n)$ が $x$ に収束する (converge) とは， $x$ の任意の開近傍 $U$ に対し，ある $N\ge 1$ が存在して， $n\ge N\implies x_n \in U$ となることを言います。これを， $(x_n)$ is eventually in $U$ ということがあります。明らかに収束点は集積点です。

証明

1. $\implies$ 2.について

$x$ が $(x_n)$ の集積点とする。 $X$ は第一可算なので， $x$ の可算な基本近傍系 $\{U_m\}$ を

U_1\supset U_2\supset U_3\supset\cdots

となるようにとる。 $\{x_n \mid n\ge 1\}\cap U_1\ne \emptyset$ より， $x_{n_1}\in U_1$ となるような $n_1\ge 1$ をとる。続いて， $\{x_n \mid n>n_1\}\cap U_2\ne \emptyset$ より， $x_{n_2}\in U_2$ となるような $n_2> n_1$ をとる。続いて $\{x_n \mid n> n_2\}\cap U_3\ne \emptyset$ より， $x_{n_3}\in U_3$ となるような $n_3>n_2$ をとる。

このように帰納的に点列 $(x_{n_k})_k$ を定めると， $x_{n_k}\to x$ である。

2. $\implies$ 1.について

背理法で示す。 $x$ が $(x_n)$ の集積点でないとすると，ある $x$ の開近傍 $U$ と $N\ge 1$ があって， $x_n \notin U \;(n\ge N)$ とできる。よって， $x_n$ の部分列が $x$ に収束することはない。

証明終

2. $\implies$ 1.の証明は， $X$ が第一可算でなくてもそのまま通用します。

3. 閉集合と点列の存在

定理3（閉集合と点列の存在）

$(X,\mathcal{O})$ を第一可算な位相空間とし， $A\subset X$ とする。このとき，次の2つは同値である。

$x\in \overline{A}$
ある点列 $(x_n)\subset A$ が存在して， $x_n\to x$ とできる

なお，第一可算でないと2. $\implies$ 1.しか言えない。後の例4.で紹介する。

証明

1. $\implies$ 2.について

$x\in\overline{A}$ とすると， $x$ の任意の開近傍 $U$ に対し， $U\cap A\ne\emptyset$ となる。 $X$ は第一可算なので， $x$ における可算な基本近傍系を

U_1\supset U_2\supset U_3\supset\cdots

とする。各 $n \ge 1$ に対し， $x_n\in U_n\cap A$ をとると，点列 $(x_n)$ は $x_n\to x$ となる。

2. $\implies$ 1.について

定理2より， $x$ は $(x_n)$ の集積点である。よって， $x$ の任意の開近傍 $U$ に対して， $(x_n)\cap U\ne \emptyset$ であるから， $A\cap U\ne \emptyset$ である。ゆえに $x\in \overline{A}$ である。

証明終

4. 開集合・閉集合の点列の特徴づけ

定理4（開集合・閉集合の点列の特徴づけ）

$(X,\mathcal{O})$ を第一可算な位相空間とし， $A\subset X$ とする。このとき，

$A$ が開集合である $\iff x_n\to x\in A$ となる任意の点列 $(x_n)\subset X$ に対し，ある $N\ge 1$ が存在して， $x_n \in A \; (n\ge N)$ とできる(すなわち $(x_n)$ is eventually in $A$ )
$A$ が閉集合である $\iff x_n\to x$ となる任意の点列 $(x_n)\subset A$ に対し， $x\in A$ となる

なお，第一可算でないと1.も2.も $\implies$ しか言えない。1.は後の例4.，2.は後の例5.で紹介する。

開集合・閉集合が点列で記述できるという定理です。

証明

1.の $\implies$ について

$A$ は $x$ の開近傍であり，収束の定義から明らか。

1.の $\impliedby$ について

$A$ が開集合でないとすると， $x\in A\setminus \operatorname{Int}(A)$ が取れる。ただし， $\operatorname{Int}(A)$ は $A$ の内部(開核)を表す。すなわち $x$ は $A$ の境界である。よって， $x\in \overline{X\setminus A}$ である。

したがって，定理3から $( x_n)\subset X\setminus A$ で， $x_n \to x$ となるものが取れる。これは， $(x_n)$ is eventually in $A$ となっていないので仮定に矛盾する。

2.の $\implies$ について

もし $x\notin A$ すなわち $x\in X\setminus A$ であるとすると， $X\setminus A$ は開集合なので，1.の $\implies$ より， $(x_n)$ is eventually in $X\setminus A$ となるが，これは $(x_n)\subset A$ という仮定に矛盾する。

2.の $\impliedby$ について

$A$ が閉集合でないとすると， $x\in \overline{A}\setminus A$ が取れる。特に， $x\in \overline{A}$ である。したがって，定理3から $( x_n)\subset A$ で， $x_n \to x$ となるものが取れるが， $x_n \to x\notin A$ となって仮定に矛盾する。

証明終

5. 連続写像の点列の特徴づけ

定理5（連続写像の点列の特徴づけ）

$(X,\mathcal{O}_X), (Y,\mathcal{O}_Y)$ を位相空間とし， $X$ を第一可算，かつ $f\colon X\to Y$ とする。このとき，以下は同値である。

$f$ は連続である
任意の $x\in X$ と任意の点列 $(x_n)\subset X$ に対し， $x_n \to x\implies f(x_n)\to f(x)$ (点列連続)

なお，第一可算でないと1. $\implies$ 2.しか言えない。

よく関数 $f\colon \R\to \R$ が $x\in \R$ で連続であることを示すのに， $x_n \to x$ となる任意の点列に対し， $\lim_{n\to\infty } f(x_n)=f(x)$ となることを示すことがありますが，これは連続性と点列連続性が同値であることを暗に使っています。

定理4の証明や反例の紹介は以下の記事で行っています。

6. 第一可算な位相空間の直積

定理6（第一可算な位相空間の直積）

第一可算な位相空間の高々可算個の直積はまた第一可算である。一方で，非可算個の直積は第一可算とは限らない。

証明

$n\ge 1$ に対し， $(X_n, \mathcal{O}_n)$ を第一可算な位相空間とし，直積 $X=\prod_{n}^\infty X_n$ に対し， $x=(x_n)\in X$ とする。 $x_n\in X_n$ における可算な基本近傍系を $\mathcal{B}_n$ とする。このとき， $x$ の基本近傍系は， $k\ge 1,\, n_1,\ldots, n_k\ge 1,\, B_{n_1}\in\mathcal{B}_{n_1},\ldots, B_{n_k}\in \mathcal{B}_{n_k}$ を用いて，

B_{n_1}\times \cdots \times B_{n_k} \times \prod_{n\ne n_1, \ldots, n_k} X_n

の形にかける集合全体である。可算集合の可算個の和集合は可算集合であるから，このような集合全体は可算個なので， $X$ も第一可算である。

一方で，たとえば，第二可算な空間 $I=[0,1]$ の非可算個の直積 $I^I$ は第一可算でない(→I^I の位相的性質～コンパクトだが点列コンパクトでない例～)。

証明終

第一可算な空間やそうでない空間の具体例

性質より具体例をみて，イメージを膨らませましょう。

例1( $\R$ ).

実数全体の集合 $\R$ は通常の位相で第一可算である。

$\R$ は距離空間であり，定理1より第一可算です。具体的には， $x\in \R$ に対し， $\{(x-1/n, x+1/n)\}_n$ は可算な基本近傍系です。

例2(密着位相).

密着空間 $(X, \{\emptyset, X\})$ は第一可算である。実際，任意の $x\in X$ に対し， $\{X\}$ は $x$ の基本近傍系である。

明らかですね。

例3(離散位相).

離散空間 $(X, 2^X)$ は第一可算である。実際，任意の $x\in X$ に対し， $\{x\}$ は $x$ の基本近傍系である。

例2.や例3.から分かる通り，第一可算は「各点についての性質」ですから，位相が大きくても小さくても（細かくても粗くても）第一可算になることがあります。

他にも，定理1で取り上げた通り，距離空間は全て第一可算です。

ここからは第一可算でないものも紹介しましょう。

例4(補有限位相・補可算位相).

$X$ を非可算集合とする。

\mathcal{O}_f=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\}

とすると， $(X,\mathcal{O}_f)$ は位相空間になる。この位相を補有限位相 (cofinite topology, finite complement topology) という。

\mathcal{O}_c=\{\emptyset \}\cup \left\{O\subset X\middle|\begin{gathered} X\setminus O \text{ is at most} \\ \text{countable}\end{gathered}\right\}

とすると， $(X,\mathcal{O}_c)$ は位相空間になる。この位相を補可算位相 (cocountable topology, countable complement topology) という。

$(X,\mathcal{O}_f)$ や $(X,\mathcal{O}_c)$ は第一可算でない。

$x\in X$ とします。 $y\ne x$ に対し， $X\setminus \{y\}$ は $x$ の開近傍であり， $\bigcap_{y\ne x} X\setminus \{y\}=\{x\}$ です。

ここで，もし $x$ で高々可算な基本近傍系 $\mathcal{B}_x$ をもつとすると，各 $y\ne x$ に対し， $x\in B\subset X\setminus\{y\}$ となる $B\in \mathcal{B}_x$ があるはずなので，上の議論より $\bigcap_{B\in\mathcal{B}_x} B = \{x\}$ でなければならないです。一方，両辺これの補集合を取ると，

\bigcup_{B\in\mathcal{B}_x} X\setminus B=X\setminus\{x\}

となりますが， $X$ には補有限位相(resp. 補可算位相)が入っているので， $X\setminus B$ は有限集合(resp. 高々可算集合)です。今の仮定より，左辺は可算個の和集合なので，左辺は高々可算集合です。一方で，右辺はそうなっていないので，矛盾していますね。よって， $X$ は第一可算ではありません。

補可算位相 $(X,\mathcal{O}_c)$ における点列の収束について考えましょう。 $x_n\to x$ となるとき， $\bigl(X\setminus (x_n)\bigr)\cup \{x\}$ も $x$ の開近傍なので， $(x_n)$ is eventually in $\bigl(X\setminus (x_n)\bigr)\cup \{x\}$ となります。よって，補可算位相について点列 $(x_n)$ が収束するならば，eventually constant，すなわちある $N\ge 1$ が存在して， $x_n=x \;(n\ge N)$ とならなければなりません。

補可算位相 $(X,\mathcal{O}_c)$ は，第一可算でないときの定理3の1. $\implies$ 2.の反例になっています。たとえば， $A\subset X$ を非可算とすると， $\overline{A}=X$ ですが，点列 $(x_n)\subset A$ が $x$ に収束するならばeventually constantなので，必ず $x\in A$ となってしまいます。

また，補可算位相 $(X,\mathcal{O}_c)$ は第一可算でないときの定理4.1の $\impliedby$ の反例にもなっています。なぜなら， $A\subset X$ を空でない任意の部分集合としたとき，点列 $(x_n)\subset X$ が $x_n \to x\in A$ となるなら，eventually constantなので， $(x_n)$ is eventually in $A$ と言えるからです。

さらに，補可算位相 $(X,\mathcal{O}_c)$ は第一可算でないときの定理5の2. $\implies$ 1.の反例にもなっています。これは，位相空間における点列連続性と点列連続だが連続でない例で紹介しています。

補有限位相・補可算位相の性質は，以下でも取り上げています。

例5(順序位相).

$\omega_1$ を最小の非可算順序数とし， $\omega_1+1=[0,\omega_1]$ における順序位相を考える。このとき，この空間は第一可算でない。

順序数における順序位相については，以下の記事で解説しています。

例5.において， $[0,\omega_1)\subset [0,\omega_1]$ は閉集合ではありませんが，「点列 $(x_n)\subset [0,\omega_1)$ が $x_n \to x$ ならば $x\in [0,\omega_1)$ 」は成立します。よって，第一可算でないときの定理4.2の $\impliedby$ の反例になっています。

例6.

$0$ 以上の整数全体の集合を $\mathbb{Z}_{\ge 0}$ とし，直積 $X=\mathbb{Z}_{\ge 0}\times \mathbb{Z}_{\ge 0}$ を考える。 $X$ における部分集合 $O\subset X$ に対し，

$(0,0)\notin O$
$(0,0)\in O$ のときは，有限個を除く $x\in \mathbb{Z}_{\ge 0}$ に対し， $\{ y \in \mathbb{Z}_{\ge 0} \mid (x, y)\notin O\}$ が有限集合になる

のいずれかが成立するような部分集合 $O\subset X$ 全体を $\mathcal{O}$ とすると， $(X,\mathcal{O})$ は位相空間になる。

この空間における $X \setminus \{(0,0)\}$ は可算集合であり，番号付けにより点列 $\bigl((x_n, y_n)\bigr)$ とみると， $(0,0)$ はこの点列の集積点であるが， $(0,0)$ に収束する部分点列は存在しない。よって定理2が成立しないので，第一可算でない。

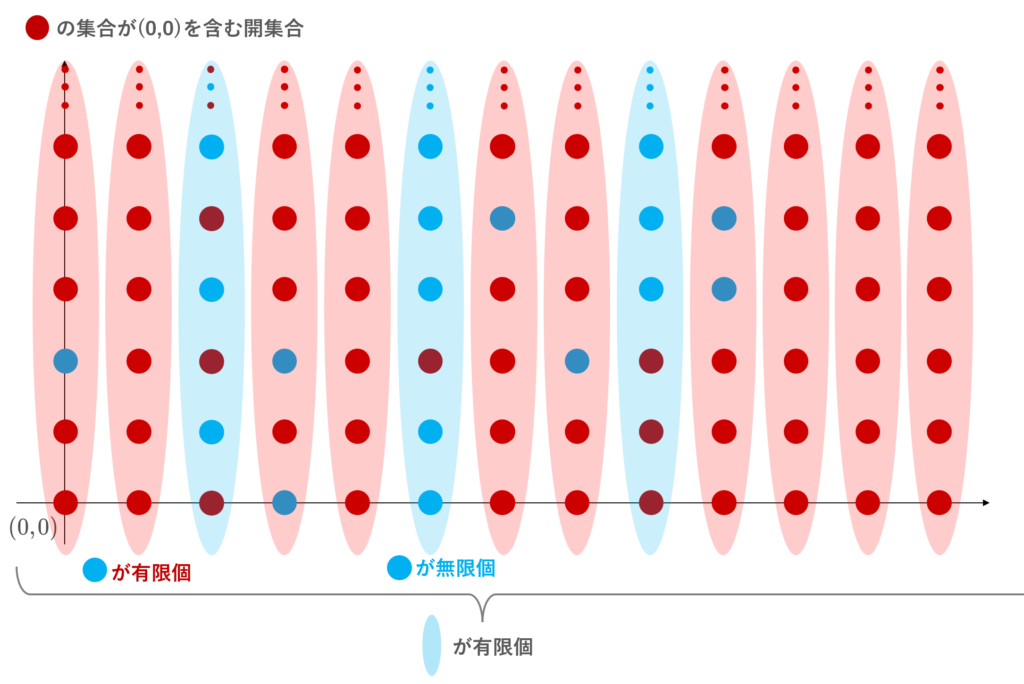
この例は，第一可算でないときの定理2の1. $\implies$ 2.の反例になっています。

$(0,0)$ が集積点であることは明らかでしょう。ここで，任意の点列 $\bigl((x_n, y_n)\bigr)\subset X\setminus \{(0,0)\}$ で， $(0,0)$ に収束するものが存在しないことを示しましょう。

$X\setminus \{(0,0)\}$ における点列で， $(0,0)$ に収束するものがない証明

背理法により，点列 $\bigl((x_n, y_n)\bigr)\subset X\setminus \{(0,0)\}$ が $(0,0)$ に収束すると仮定する。 $k\ge 1$ に対し， $U_k=X\setminus(\{k\} \times \mathbb{Z}_{\ge 0} )$ とすると， $U_k$ は $(0,0)$ の開近傍である。

よって背理法の仮定より，ある $N_k \ge 1$ が存在して， $n\ge N_k\implies (x_n, y_n)\in U_k$ （すなわち $\bigl((x_n, y_n)\bigr)$ is eventually in $U_k$ ）ゆえに， $x_n =k$ となる $n\in\mathbb{Z}_{\ge 0}$ は有限個しかない。

ここで， $U=X\setminus \bigl((x_n, y_n)\bigr)$ と定める。このとき， $(0,0)\in U$ であり，かつ上の議論より，各 $k\in\mathbb{Z}_{\ge 0}$ に対し， $\{ y \in \mathbb{Z}_{\ge 0} \mid (k, y)\notin U\}$ が有限集合になる。よって $U$ は $(0,0)$ の開近傍である。しかし，任意の $n\ge 1$ で $(x_n, y_n)\notin U$ なので，これは点列 $\bigl((x_n, y_n)\bigr)$ が $(0,0)$ に収束することに矛盾する。

したがって，題意は示された。

証明終

なお，ネット(有向点族)の話を知っていれば，「ネットが集積点をもてば，その点に収束する部分ネットがある」ことが知られていますから，今回の例は，点列が収束部分列をもたないが，収束部分ネットはもつような例になっています。収束部分ネットの取り方は，ネット(有向点族)による位相空間論と点列との比較における，「ネットが集積点をもてば，その点に収束する部分ネットがある」の証明を読めばおおよそ分かるでしょう。