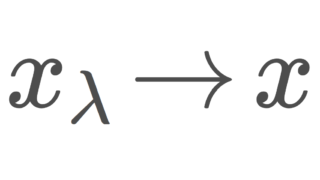位相空間におけるフィルターとは,収束の概念を集合族によって記述する概念であり,ネット(有向点族)と並んで,位相空間の性質を収束という観点から扱うのに有用なツールです。
本サイトでは位相空間におけるフィルターの概念と,それによって記述される位相的性質を証明付きで紹介しましょう。
1. フィルターの定義と具体例
まずは,フィルター・自由フィルター・フィルター基・超フィルターなどの基本的な概念の定義と具体例を一気に紹介しましょう。
フィルターの定義
フィルター自体は,位相空間でなくても定義できます。
定義1(フィルター・自由フィルター・細分)
X を空でない集合とする。 X の空でない部分集合族 \emptyset\ne \mathscr{F}\subset 2^X ( 2^X はべき集合)が X 上のフィルター (filter) であるとは,
- \large\color{red} \emptyset \notin \mathscr{F}
- \large\color{red} F_1, F_2\in\mathscr{F}\implies F_1\cap F_2\in\mathscr{F}
- \large\color{red} F\in\mathscr{F}, \, F\subset F'\implies F'\in\mathscr{F}
の全てが成立することを言う。
X 上のフィルター \mathscr{F} が \bigcap_{F\in\mathscr{F}} F=\emptyset をみたすとき,\mathcal{F} は自由 (free) であるという。
X 上のフィルター \mathscr{F},\mathscr{G} に対し,\mathscr{F}\subset \mathscr{G} が成立するとき,\mathscr{G} は \mathscr{F} の細分 (refinement) であるという。
1.と2.より,任意の F_1, F_2\in\mathscr{F} に対して, F_1\cap F_2\ne \emptyset でなければなりません。これは大事なことです。また3.より明らかに X\in\mathscr{F} です。
自由でないフィルター,すなわち \bigcap_{F\in\mathscr{F}} F\ne \emptyset をみたすフィルター \mathscr{F} を固定された (fixed) ということもあります。
例を挙げましょう。
フィルターの簡単な具体例
例1.
A\subset X を空でないとするとき,
\mathscr{F}=\{ F\subset X\mid A\subset F\}
とすると,これはフィルターである。
これは, \bigcap_{F\in\mathscr{F}} F=A\ne\emptyset なので,自由でないフィルターです。
例2.
(X,\mathcal{O}) を位相空間とし, A\subset X を空でないとする。
\mathscr{F}=\{F\subset X\mid A\subset\operatorname{Int}(F)\}
とすると,これはフィルターである。ただし, \operatorname{Int}(A) は A の内部(開核)を表す。特に A=\{a\} であるとき, \mathscr{F} は a の近傍系(近傍全体の集合)になる。
例1.とほぼ同じですが,例1.は A\in \mathscr{F} だったのに対し,今回はそうとは限りません。
これは, \bigcap_{F\in\mathscr{F}} F\supset A なので,自由でないフィルターです。
近傍系も一種のフィルターなので,フィルターの性質1.から3.は,近傍系がみたす性質より緩いです。
例3(フレシェフィルター).
X を無限集合とし,
\mathscr{F}=\{F\subset X\mid X\setminus F\text{ is finite}\}
は自由フィルターである。これをフレシェフィルター (Fréchet filter) または補有限フィルター (cofinite filter) という。
フィルター基の定義と具体例
近傍系(近傍全体の集合)に対応する基本近傍系の概念があるように,フィルターにも対応するフィルター基という概念があります。定義しましょう。
定義2(フィルター基)
X を空でない集合とし,\mathscr{F} を X 上のフィルターとする。
\mathscr{C}\subset \mathscr{F} がフィルター基 (filter base) であるとは,任意の F\in \mathscr{F} に対して,ある C\in \mathscr{C} が存在して,
\Large\color{red} C\subset F
とできることをいう。
フィルター基の取り方は一通りではありません。たとえば,\mathscr{F} そのものは \mathscr{F} のフィルター基であるし,前述の例1.のように, \mathscr{F}=\{ F\subset X\mid A\subset F\} のときは, \mathscr{C}=\{A\} もフィルター基です。
逆に,部分集合族が与えられたときに,それをフィルター基とするフィルターを生成できるでしょうか。それの答えが以下の定理です。
定理1.1(フィルター基からのフィルターの生成)
X を空でない集合とし,\emptyset\ne \mathscr{C}\subset 2^X を空でない部分集合族とする。
\mathscr{C} が,あるフィルター \mathscr{F} のフィルター基となる必要十分条件は,
- \emptyset\notin \mathscr{C}
- C_1, C_2\in\mathscr{C} ならば,ある C\in\mathscr{C} が存在して, C\subset C_1\cap C_2 とできる
の両方が成り立つことである。このとき,
\mathscr{F}=\{F\subset X\mid \exists C\in\mathscr{C},\, C\subset F\}
となり,\mathscr{F} を,\mathscr{C} によって生成される (generated) フィルターといい,本記事では \large\color{red} \mathscr{F}(\mathscr{C}) とかく。
なお, \mathscr{D} が,有限交叉性をもつ,すなわち任意の有限個の D_1, \ldots, D_n\in\mathscr{D} が D_1\cap \cdots\cap D_n\ne\emptyset をみたすとき,
\mathscr{C}= \left\{D_1\cap \cdots\cap D_n\mid n\ge 1,\, D_1, \ldots, D_n\in\mathscr{D} \right\}
はフィルター基の条件をみたします。このときの \mathscr{F}(\mathscr{C}) を本記事では \large\color{red} \mathscr{F}(\mathscr{D}) とかき,\mathscr{D} によって生成される (generated) フィルターということにします。
定理1.1の証明
フィルター基 \implies 1,2.について
\mathscr{C} がフィルター \mathscr{F} のフィルター基とすると, \mathscr{C}\subset \mathscr{F} より,1.が成り立っていなければならず,また, C_1,C_2\in \mathscr{C}\subset \mathscr{F} に対し, C_1\cap C_2\in\mathscr{F} であるから,フィルター基の定義より,2.が成り立たなければならない。
1,2.\implies あるフィルターのフィルター基について
フィルターの定義より,\mathscr{C} がフィルター基なら生成されるフィルターは \mathscr{F}=\{F\subset X\mid \exists C\in\mathscr{C},\, C\subset F\} を含む。
\mathscr{F} がフィルターであることを示そう。 \emptyset \notin \mathscr{F} と F\in\mathscr{F}, \, F\subset F'\implies F'\in\mathscr{F}は明らか。 F_1, F_2\in\mathscr{F} とすると, C_1\subset F_1,\, C_2\subset F_2 をみたすある C_1, C_2\in\mathscr{C} が存在する。このとき,条件2.より,ある C\in\mathscr{C} が存在して,
C\subset C_1\cap C_2\subset F_1\cap F_2
であり, \mathscr{F} の定義より, F_1\cap F_2\in\mathscr{F} である。したがって,\mathscr{F} はフィルターである。
\mathscr{C} が \mathscr{F} のフィルター基であることは, \mathscr{F} の定め方より明らか。よってすべて示せた。
証明終
例4.
\R 上の集合族
\mathscr{C}=\{ (a,\infty)\mid a\in\R\}
はフィルター基の条件(定理1.1中の1.と2.)をみたす。\mathscr{C} によって生成されるフィルターは
である。これは自由フィルターである。
なので,自由フィルターです。このフィルターは, \bigl(\mathbb{Q}\cap (0,1)\bigr)\cup (2,\infty)\in\mathscr{F} ですが, (0,1)\notin \mathscr{F} です。
例5.
\R 上の集合族
\mathscr{C}=\left\{ \left(0,\frac{1}{n}\right)\middle| n\ge 1 \right\}
はフィルター基の条件をみたす。\mathscr{C} によって生成されるフィルターは
である。これは自由フィルターである。
例6.
(X,\mathcal{O}) を位相空間とし, x\in X とする。
\mathcal{B}_x を x における基本近傍系とすると, \mathcal{B}_x はフィルター基の条件をみたす。\mathcal{B}_x によって生成されるフィルターは, x の近傍系(近傍全体の集合) \mathcal{N}_x である。
x\in \bigcap_{N\in\mathcal{N}_x} N なので,これは自由でないフィルターです。
例7( f(\mathscr{F})).
(X,\mathcal{O}_X),(Y,\mathcal{O}_Y) を位相空間とし, f\colon X\to Y を写像とする。
X 上のフィルター \mathscr{F} に対し,
\mathscr{C}_Y= \{ f(F)\mid F\in\mathscr{F}\}
は Y 上のフィルター基の条件をみたす。\mathscr{C}_Y によって生成されるフィルター \mathscr{F}(\mathscr{C}_Y) を \large\color{red} f(\mathscr{F}) とかく。
f は連続でなくてもかまいません。連続である必要十分条件は,後の定理2.3で述べます。
\mathscr{C}_Y 自体がフィルターとは言えません。 f が全射でないと, X\in \mathscr{C}_Y にならないです。フィルター基であること(定理1.1の1.と2.をみたすこと)は簡単に示せます。
フィルターの収束・集積点と具体例
フィルターは収束の概念を扱うために有用なツールです。
定義3(フィルターの収束・集積点)
(X,\mathcal{O}) を位相空間とし, x\in X とする。また, x の近傍系(近傍全体の集合)を \mathcal{N}_x とする。
X 上のフィルター \mathscr{F} が x に収束する (converge) とは,
\Large \color{red} \mathcal{N}_x\subset \mathscr{F}
すなわちフィルター \mathscr{F} が近傍系 \mathcal{N}_x の細分になっていることをいう。これを,\large\color{red}\mathscr{F}\to x とかく。
また,任意の F\in\mathscr{F} と任意の N\in \mathcal{N}_x に対して,
\Large\color{red}F \cap N\ne \emptyset
となるとき,\mathscr{F} は x を集積点 (accumulation point, cluster point) にもつという。これは, x\in \bigcap_{F\in \mathscr{F}} \overline{F} となることと同値である。
\mathcal{N}_x\subset \mathscr{F} とかくのと \mathscr{F}\to x とかくのはそんなに労力が変わらない気がしますが,「収束」的なかき方をします。
明らかにフィルター \mathscr{F} が x に収束すれば, x を集積点にもちます。
例を見ましょう。
例8.
(X,\mathcal{O}) を2点以上の点をもつ位相空間とし, x\in X,\, A\subset X とする。
\mathscr{F}_x=\{ F\subset X\mid x\in F\}
とすると,これはフィルターで,位相によらず \mathscr{F}_x\to x である。 X が密着空間なら,任意の y\in X に対して,\mathscr{F}_x\to y である。
とすると,これはフィルターである。ある x\in X に対し, x の任意の近傍が A を含むとき, \mathscr{F}_A\to x である。そのような x が存在しないときは, \mathscr{F}_A は収束点をもたない。一方で,任意の a\in A は \mathscr{F}_A の集積点である。
\mathscr{F}_x\to x とは \mathcal{N}_x\subset \mathscr{F}_x のこと,\mathscr{F}_x\to y とは \mathcal{N}_y\subset \mathscr{F}_x のことであったことに注意してください。
密着位相のときは, y\notin F となる F\in\mathscr{F}_x があったとしても, \mathscr{F}_x\to y となります。また,一般に収束先は1点とは限りません。
例9(\R).
例5.で取り上げた \R 上のフィルター基
\mathscr{C}=\left\{ \left(0,\frac{1}{n}\right)\middle| n\ge 1 \right\}
において,\mathscr{F}(\mathscr{C})\to 0 である。
すなわち,\mathcal{N}_0\subset \mathscr{F}(\mathscr{C}) です。フィルター基 \mathscr{C} は 0 を含むものはありませんが,生成されるフィルターが 0 に収束するのはあり得るわけです。また,\mathscr{F}(\mathscr{C}) は自由フィルターです。自由フィルターでも収束することがあるということです。
例10(補有限位相).
X を無限集合とし,
\mathcal{O}_f=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\}
とすると, (X,\mathcal{O}_f) は位相空間となる。これを補有限位相 (cofinite topology) という。さらに,
を例3.で述べたようにフレシェフィルターとする。このとき,任意の x に対し, \mathscr{F}\to x となる。
例10.も,例9.と同じく,自由フィルターでも収束することがある例になっています。
補有限位相については,補有限位相と補可算位相について掘り下げるでも解説しています。
超フィルター(極大フィルター)
続いて,超フィルターについて定義しましょう。フィルターを扱う上で欠かせない,興味深い概念です。
定義4(超フィルター・極大フィルター)
X を空でない集合とし, \mathscr{F} を X 上のフィルターとする。
\mathscr{F}\subsetneq \mathscr{G} となるフィルター \mathscr{G} が存在しないとき, \mathscr{F} を超フィルター (ultrafilter) または極大フィルター (maximal filter) という。
日本語で述べると,細分が自分自身以外に存在しないフィルターを超フィルターといいます。
例11(自由でない超フィルター).
X を空でない集合とし, \mathscr{F} を X 上の自由でないフィルターとする。 x\in\bigcap_{F\in\mathscr{F}} F に対し,
\mathscr{F}_x= \{ F\subset X\mid x\in F\}
とするとき,\mathscr{F}\subset \mathscr{F}_x であり,\mathscr{F}_x は超フィルターである。特に,自由でない超フィルターは \mathscr{F}_x \; (x\in X) の形に限る。
特に, (X,\mathcal{O}) を位相空間とするとき, x\in X に収束する超フィルターは \mathscr{F}_x に限る。
ここで重要な定理は次です。
定理1.2(超フィルターの性質)
X を空でない集合とし, \mathscr{F} を X 上のフィルターとする。このとき,次の3つが成立する。
- \mathscr{F}\subset \mathscr{F}' で,\mathscr{F}' が超フィルターであるものが常に存在する。
- \mathscr{F} が超フィルターである必要十分条件は,任意の A\subset X に対し, A\in \mathscr{F} または X\setminus A\in\mathscr{F} のいずれかが必ず成立することである。
- 超フィルター \mathscr{F} が x\in X を集積点にもてば \mathscr{F}\to x である。
1.はすなわち,任意のフィルターは超フィルターを細分にもつということです。証明には選択公理と同値なツォルンの補題を使います。
証明
1.について
\mathfrak{F}=\{ \mathscr{G}\colon \text{ filter} \mid \mathscr{F}\subset \mathscr{G}\} を,\mathscr{F} を含むフィルター全体の集合とすると,これは包含関係 \mathscr{F}_1\le \mathscr{F}_2\iff\mathscr{F}_1\subset \mathscr{F}_2 によって帰納的半順序集合であることが容易に示せる。ツォルンの補題より, \mathfrak{F} には少なくとも一つの極大元 \mathscr{F}' が存在する。
2.の \implies について
A\subset X とする。このとき,「任意の F\in\mathscr{F} に対して, F\cap A\ne \emptyset」か「任意の F\in\mathscr{F} に対して, F\cap (X\setminus A)\ne \emptyset」のいずれかが必ず成立する。実際,F_1, F_2\in \mathscr{F} が, F_1\cap A=F_2\cap (X\setminus A)=\emptyset が成り立つとすると, F_1\cap F_2=\emptyset となるから,フィルターの定義に矛盾する。
よって,「任意の F\in\mathscr{F} に対して, F\cap A\ne \emptyset」が成立すると仮定する。
\mathscr{C}=\{ F\cap A\mid F\in\mathscr{F}\}
とすると,これはフィルター基の条件をみたす。 A\in \mathscr{F}(\mathscr{C}) かつ \mathscr{F}\subset \mathscr{F}( \mathscr{C}) であるが,\mathscr{F} の極大性より,\mathscr{F}= \mathscr{F}( \mathscr{C}) である。よって,A\in\mathscr{F} であるから,題意は示された。
2.の \impliedby について
\mathscr{F} が超フィルターでないと仮定する。\mathscr{F}\subsetneq \mathscr{G} をフィルターとすると, A\notin \mathscr{F} かつ A\in \mathscr{G} となる A\subset X が取れる。
\mathscr{F} の仮定より, X\setminus A\in\mathscr{F} である。よって,A, X\setminus A\in\mathscr{G} であるが,
A\cap (X\setminus A)=\emptyset
となり,これは \mathscr{G} がフィルターであることに矛盾する。よって,\mathscr{F} は超フィルターである。
3.について
後の定理2.1と超フィルターの定義から明らか。
証明終
任意のフィルターがそれを含む超フィルターをもつので,自由フィルターも超フィルターをもつはずです。文献[1]いわく,自由な超フィルターで,具体的に構成されたものはまだ存在しないとのことです。神秘的ですね。
定理1.3(フィルターと写像)
(X,\mathcal{O}_X),(Y,\mathcal{O}_Y) を位相空間とし, f\colon X\to Y を写像とする。
\mathscr{F} を X 上の超フィルターとすると, f(\mathscr{F}) は Y 上の超フィルターである。
f(\mathscr{F}) の定義は例7.にあります。定理1.3の証明は,定理1.2.2を使えばほぼ明らかです。 f は連続でなくても構いません。
2. フィルターと位相的性質
さてここからは,フィルターによって記述できる位相的性質についてみていきましょう。
1. フィルターの集積点 ⇔ 収束する細分をもつ
定理2.1(フィルターの集積点 ⇔ 収束する細分をもつ)
(X,\mathcal{O}) を位相空間とし,\mathscr{F} をその上のフィルターとする。このとき,以下は同値である。
- x\in X が \mathscr{F} の集積点である
- x\in X に収束する \mathscr{F} の細分となるフィルターをもつ
特に,超フィルター \mathscr{F} が1.または2.の条件をみたすとき,\mathscr{F}\to x である。
超フィルターは,自分自身より大きな細分をもたないので,2.を仮定すれば x に収束するのは明らかです。1.と2.の同値性を示しましょう。
証明
1.\implies 2.について
\mathscr{C}=\{ N\cap F\mid N\in \mathcal{N}_x, \, F\in\mathscr{F}\}
とすると,これはフィルター基の条件をみたし,\mathscr{F}(\mathscr{C}) が2.をみたす。
2.\implies 1.について
もし,\mathscr{F}\subset\mathscr{G}\to x とすると,収束の定義より \mathcal{N}_x\subset \mathscr{G} である。 F\in\mathscr{F},\, N\in\mathcal{N}_x とすると,どちらも \mathscr{G} の元なので, F\cap N\ne\emptyset である。ゆえに,\mathscr{F} は x を集積点にもつ。
証明終
2. フィルターと閉集合
定理2.2(フィルターと閉集合)
(X,\mathcal{O}) を位相空間とし,A\subset X とする。このとき,以下は同値である。
- x\in\overline{A}
- X 上のフィルター \mathscr{F} で,A\in \mathscr{F} かつ \mathscr{F}\to x となるものが存在する
証明
1.\implies 2.について
x\in \overline{A} ならば,任意の N\in \mathcal{N}_x に対し, N\cap A\ne\emptyset となることに注意する。このとき,
\mathscr{C}=\{ N\cap A\mid N\in\mathcal{N}_x\}
はフィルター基の条件をみたし,A\in \mathscr{F}(\mathscr{C})\to x である。
2.\implies 1.について
X 上のフィルター \mathscr{F} が A\in \mathscr{F} \to x と仮定すると,定理2.1より,\mathscr{F} は x を集積点にもつので明らか。
証明終
3. フィルターと連続写像
定理2.3(フィルターと連続写像)
(X,\mathcal{O}_X),(Y,\mathcal{O}_Y) を位相空間とし, x\in X,\, f\colon X\to Y とする。このとき,次は同値である。
証明
1.\implies 2.について
\mathscr{F}\to x とすると, f は x で連続より, f(x) の任意の近傍 N に対し, f^{-1}(N)\in\mathscr{F} である。
よって, f\circ f^{-1}(N)\in f(\mathscr{F}) であり,写像の像・逆像と集合との演算証明より f\circ f^{-1}(N)\subset N なので, N\in f(\mathscr{F}) である。以上から, f(\mathscr{F})\to f(x) が言えた。
2.\implies 1.について
\mathscr{F}=\mathcal{N}_x として2.を適用する。f(\mathscr{F})\to f(x) なので, f(x) の任意の近傍 N に対し, f(M)\subset N となる M\in\mathscr{F}=\mathcal{N}_x が存在する。
M\subset f^{-1}(N) より, f^{-1}(N) は x の近傍である。よって, f は x で連続である。
証明終
4. フィルターと直積位相
定理2.4(フィルターと直積位相)
\{(X_\alpha,\mathcal{O}_\alpha)\}_{\alpha\in\Alpha} を位相空間の族とする。さらに, X=\prod_{\alpha\in\Alpha} X_\alpha における直積位相を考え, p_\alpha \colon X\to X_\alpha を自然な射影とする。
\mathscr{F} を X 上のフィルターとし, x\in X とする。このとき,次の2つは同値である。
- \mathscr{F}\to x
- 任意の \alpha\in \Alpha に対し, p_\alpha(\mathscr{F})\to p_\alpha(x)
証明
1.\implies 2.について
p_\alpha が連続であることと,定理2.3よりわかる。
2.\implies 1.について
U を x の開近傍とすると,直積位相の定義より, ある n\ge 1 と \alpha_1,\ldots, \alpha_n\in \Alpha と, U_1\in \mathcal{O}_{\alpha_1}, \ldots ,U_n\in\mathcal{O}_{\alpha_n} が存在して,
x\in \prod_{k=1}^n U_k \times\prod_{\alpha\in \Alpha\setminus\{\alpha_1,\ldots, \alpha_n\} }X_\alpha\subset U
とできる。真ん中の集合を B とする。各 \alpha\in \Alpha に対し, p_\alpha(\mathscr{F})\to p_\alpha(x) より, U_k\in p_{\alpha_k}(\mathscr{F}) である。ゆえに,ある F_k\in\mathscr{F} が存在して, p_{\alpha_k}(F_k)\subset U_k とできる。
F=\bigcap_{k=1}^n F_k とおくと,フィルターの定義から F\in\mathscr{F} であり, F\subset B\subset U より,U\in\mathscr{F} である。よって, \mathscr{F}\to x である。
証明終
5. フィルターと分離公理~収束先の一意性~
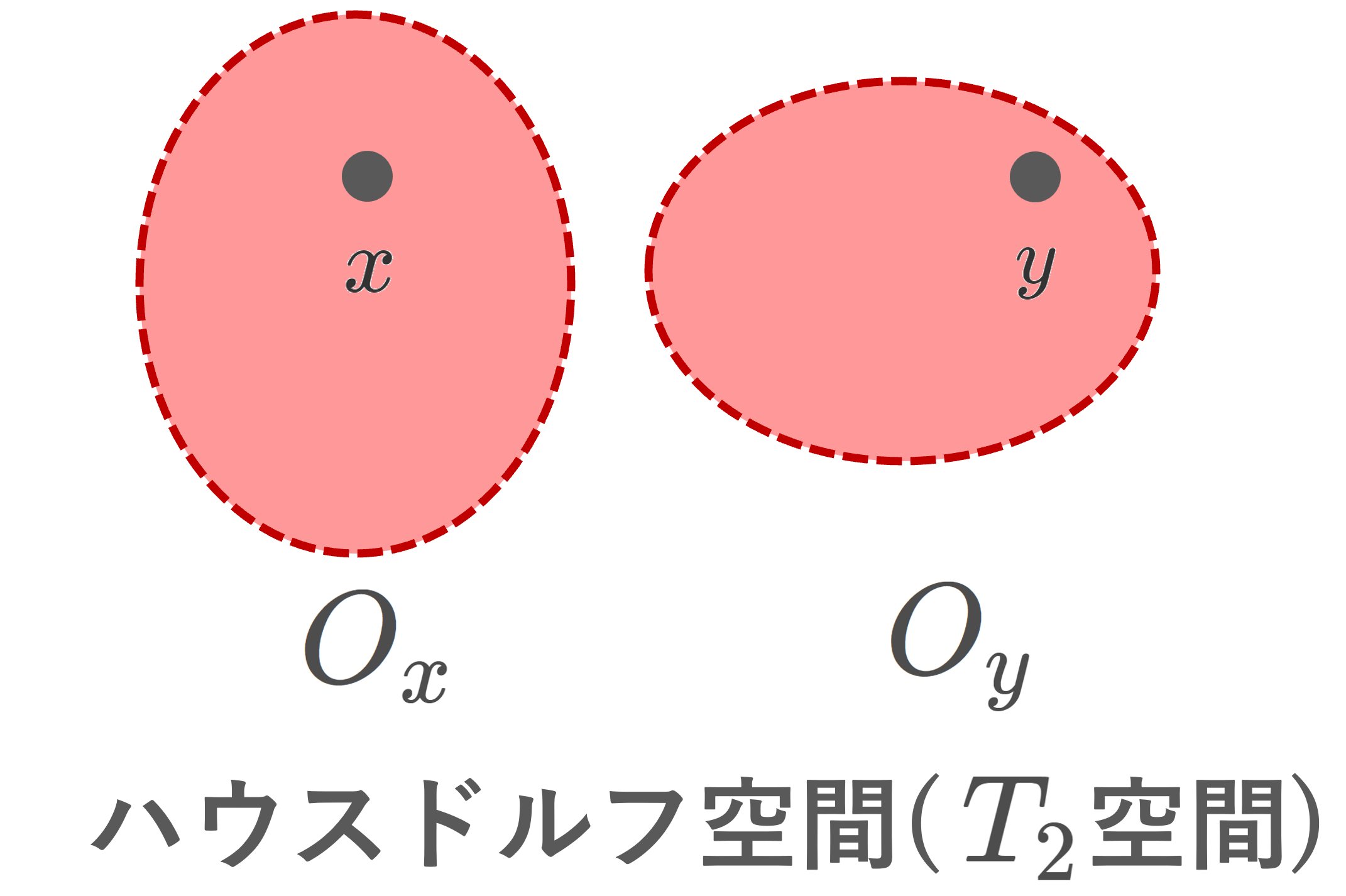
定理2.5(フィルターと分離公理~収束先の一意性~)
(X,\mathcal{O}) を位相空間とする。このとき,次の2つは同値である。
- X はハウスドルフ空間( T_2 空間)である
- フィルターが収束するとき,その収束先は必ず1点のみである
証明
1.\implies 2.について
x,y\in X に対し,\mathscr{F}\to x かつ \mathscr{F}\to y とする。このとき,\mathcal{N}_x, \mathcal{N}_y\subset \mathscr{F} であり,ハウスドルフ性の仮定より,もし x\ne y なら N_x\cap N_y=\emptyset となる N_x\in\mathcal{N}_x, \, N_y\in\mathcal{N}_y が存在して,フィルターの定義に反する。
以上から, x=y であるから,2.が言えた。
2.\implies 1.について
X がハウスドルフでないと仮定すると,ある異なる2点 x,y\in X が存在して,任意の N_x \in\mathcal{N}_x,\, N_y\in\mathcal{N}_y に対し, N_x\cap N_y\ne\emptyset とできる。
\mathscr{F}=\{ N_x\cap N_y\mid N_x \in\mathcal{N}_x,\, N_y\in\mathcal{N}_y\}
と定めると,これはフィルターであり,\mathscr{F}\to x かつ \mathscr{F}\to y である。よって,2.に矛盾する。
証明終
6. フィルターとコンパクト性
定理2.6(フィルターとコンパクト性)
(X,\mathcal{O}) を位相空間とする。このとき,以下は同値
- X はコンパクト
- X 上の任意のフィルターが集積点をもつ
- X 上の任意のフィルターが収束する細分をもつ
- X 上の任意の超フィルターが収束する
証明にあたっては,コンパクトと同値な概念である「有限交叉性があれば全体が交叉する」という話を用います。
(X,\mathcal{O}) は位相空間とする。 X がコンパクトであることと,以下は同値である。
\{F_\lambda\}_{\lambda\in \Lambda} を有限交叉性をもつ閉集合族とするとき, \bigcap_{\lambda\in\Lambda} F_\lambda\ne \emptyset が成り立つ。
すなわち,任意の有限個の \lambda_1, \ldots, \lambda_n \in \Lambda について, \bigcap_{k=1}^n F_{\lambda_k}\ne\emptyset をみたす閉集合族 \{F_\lambda\}_{\lambda\in \Lambda} に対し, \bigcap_{\lambda\in\Lambda} F_\lambda\ne \emptyset が成り立つ。
これについての証明は,コンパクト空間とコンパクト集合について詳しく内にあります。
定理2.6の証明
1.\implies 2.について
\mathscr{F} をフィルターとすると,フィルターの定義より,閉集合族 \{\overline{F}\}_{F\in\mathscr{F}} は有限交叉性をもつ。 X はコンパクトなので, \bigcap_{F\in\mathscr{F}} \overline{F} は空でない。 x\in \bigcap_{F\in\mathscr{F}} \overline{F} とすると, x は \mathscr{F} の集積点である。
2.\implies 1.について
\mathscr{C}=\{F_\lambda\}_{\lambda\in \Lambda} を有限交叉性をもつ閉集合族とする。 \mathscr{F}=\mathscr{F}( \mathscr{C}) とすると,2.の仮定より, x\in \bigcap_{F\in\mathscr{F}} \overline{F} が存在する。
x\in \bigcap_{F\in\mathscr{F}} \overline{F}\subset \bigcap_{\lambda\in\Lambda} F_\lambda
なので, \bigcap_{\lambda\in\Lambda} F_\lambda\ne\emptyset である。よって, X はコンパクトである。
2.\iff3.については,定理2.1で示した。
3. \iff 4.については,定理1.2.1から明らか。
証明終
フィルターとネット(有向点族)の関係
フィルターとネット(有向点族)は,どちらも収束の概念を扱うもので,相互に対応しています。その対応関係について述べましょう。ネット(有向点族)については既知とします。
定義4(ネットによって生成されたフィルター・フィルターによって生成されたネット)
(X, \mathcal{O}) を位相空間とする。
(x_\lambda)_{\lambda\in\Lambda} \subset X をネット(有向点族)とするとき,
C_{\lambda_0}=\{ x_\lambda\mid \lambda\ge \lambda_0\}
の形全体の集合 \mathscr{C}=\{C_{\lambda_0}\mid \lambda_0\in \Lambda\} をフィルター基とするフィルター \mathscr{F} を, (x_\lambda) によって生成された (generated) フィルターという。
\mathscr{F} を X 上のフィルターとする。 \Lambda_\mathscr{F}=\{ (x, F)\mid x\in F\in\mathscr{F}\} とすると, (x_1, F_1)\le (x_2, F_2)\iff F_2\subset F_1 により, \Lambda_\mathscr{F} は有向集合になる。
このとき, i\colon \Lambda_\mathscr{F}\to X を i(x, F)=x と定めると, ( \Lambda_\mathscr{F}, i) はネット(有向点族)である(すなわち (x)_{(x, F)\in \Lambda_\mathscr{F}} はネットである)。これを, \mathscr{F} によって生成された (generated) ネットという。
このとき,ネットとネットによって生成されたフィルター,あるいはフィルターとフィルターによって生成されたネットはさまざまな概念が対応関係にあります。対応する概念を並列に並べました。
| フィルター \mathscr{F} | ネット(有向点族) (x_\lambda) | |
|---|---|---|
| \mathscr{F}\to x | \leftrightarrow | x_\lambda \to x |
| 集積点 | \leftrightarrow | 集積点 |
| 自由なフィルター | \rightarrow | 自明でないネット (eventually constantでないネット) |
| 細分 | \leftarrow | 部分ネット |
| 超フィルター | \leftrightarrow | 普遍ネット(超ネット) |
\leftarrow とは,ネットが該当条件をみたすならば,ネットによって生成されたフィルターも対応する条件をみたすことを指します。 \rightarrow とは,フィルターが該当条件をみたすならば,フィルターによって生成されたネットも対応する条件をみたすことを指します。 \leftrightarrow は \leftarrow かつ \rightarrow の両方が成立することをいいます。
注意ですが,ネットとフィルターが1対1に対応しているわけではありません。ネットから生成されたフィルターを考えて,そのフィルターから生成されたネットを考えると,元のネットには戻ってきません。たとえば,普遍ネットの部分ネットは,ネットとしては別物ですが,生成されたフィルターは同じ超フィルターになります。なぜなら,
からです。本記事では,上の表の1番目にあたる,以下の定理を示しましょう。
定理3(フィルターとネットの収束の対応)
(X, \mathcal{O}) を位相空間とする。
証明
1.の \implies について
U を x の開近傍とすると,x_\lambda\to x より,ある \lambda_0 があって, \lambda\ge \lambda_0\implies x_\lambda\in U である。よって, C_{\lambda_0}\subset U であり, C_{\lambda_0}\in\mathscr{F} なので, U\in\mathscr{F} である。ゆえに, \mathscr{F}\to x を得る。
1.の \impliedby について
\mathscr{F}\to x と仮定する。 U を x の開近傍とすると,U\in\mathscr{F} であり,\mathscr{F} の定義から,ある \lambda_0 が存在して, C_{\lambda_0}\subset U である。
すなわち, \lambda\ge \lambda_0\implies x_\lambda\in C_{\lambda_0}\subset U であるから, (x_\lambda) is eventually in U である。よって x_\lambda\to x である。
2.の \implies について
U を x の開近傍とすると, \mathscr{F}\to x より, U\in \mathscr{F} である。ゆえに, u\in U に対し,
(v, V)\ge (u, U)\implies v\in U
であるから, (x_\lambda)_{\lambda\in \Lambda_\mathscr{F}} is eventually in U である。したがって, x_\lambda\to x が言えた。
2.の \impliedby について
U を x の開近傍とすると, x_\lambda \to x より, (x_\lambda)_{\lambda\in \Lambda_\mathscr{F}} is eventually in U である。ゆえに,ある (v, V) \in \Lambda_{\mathscr{F}} が存在して, v\in U である。
ネットの定め方より, V\in\mathscr{F} かつ V\subset U なので, U\in\mathscr{F} である。よって, \mathscr{F}\to x である。
証明終
フィルターとネットは,似たような性質が成り立ちます。以下の表を見てください。
| フィルター \mathscr{F} | ネット(有向点族) (x_\lambda) |
|---|---|
| フィルターが集積点をもつならばその点に収束する細分フィルターが存在する | ネットが集積点をもつならばその点に収束する部分ネットが存在する |
| 任意のフィルターは超フィルターを細分にもつ | 任意のネットは普遍ネットを部分ネットにもつ |
| 超フィルターが集積点をもてばその点に収束する | 普遍ネットが集積点をもてばその点に収束する |
| 集合で扱うので,開集合系による位相の定義とも親和性が高く,定義に基づいて扱いやすい | 点列の収束の一般化と考えることができ,位相を収束・連続の概念の一般化と考えたときに直感的に捉えやすい |
最後の行には,ネットとフィルターの違いと強みを載せました。