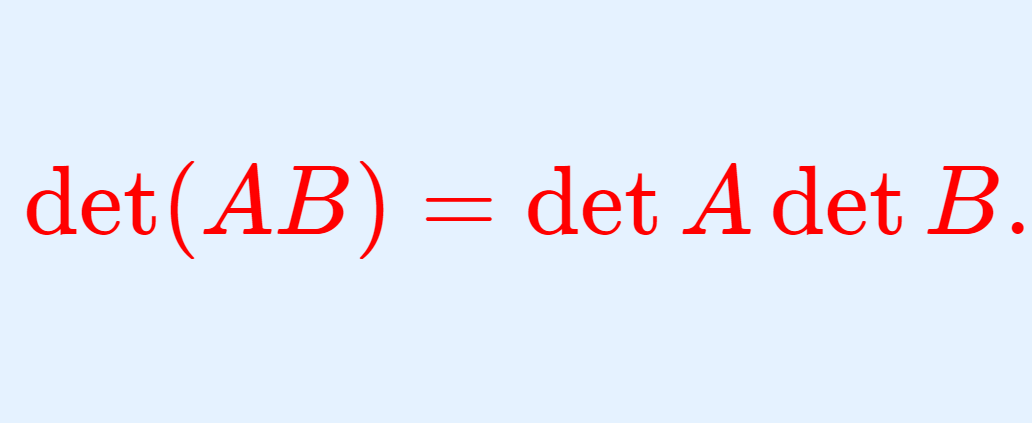行列式の性質6つの証明(列,行の線形性,置換,積,転置など)

行列式の性質のうち，特に大事な6つの性質を証明します。最後には，行列の基本変形と行列式の関連性についても考えます。

行列式の性質
行列式の性質の証明
行列の基本変形による行列式の変化
特殊で有用な行列式
1. ファンデルモンドの行列式
2. 巡回行列式

行列式の性質

まず最初に，今回紹介する行列式の性質を全て列挙しましょう。

以下で，複素数 $\mathbb{C}$ は実数 $\mathbb{R}$ に変えても成立します。

定理（行列式の性質）

1. 行列式は，各列に関して線形性がある。すなわち， $\boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n$ を $n$ 次元列ベクトル， $s,t\in \mathbb{C}$ とすると，

\small \begin{aligned} &\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{s\boldsymbol{a_k}+t\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ ={}&\textcolor{red}{s} \det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{a_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ &+ \textcolor{red}{t}\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}). \end{aligned}

また同様に，行列式は各行に関して線形性がある。すなわち， $\boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n$ を $n$ 次元行ベクトル， $s,t\in \mathbb{C}$ とすると，

\small \begin{aligned} &\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{s\boldsymbol{a_k} +t\boldsymbol{b_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} \\ &= \textcolor{red}{s}\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{\boldsymbol{a_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} +\textcolor{red}{t}\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{\boldsymbol{b_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} .\end{aligned}

2. 転置行列の行列式は元のそれと同じ。すなわち， $\color{red}\det A = \det A^\top.$

3. （列・行の入れ替え） $\sigma\in S_n$ を置換とする。このとき，太字を列ベクトルとすると，

\begin{aligned}& \det(\boldsymbol{a_{\textcolor{red}{\sigma(1)}}}, \dots ,\boldsymbol{a_{\textcolor{red}{\sigma(n)}}})\\ & =\textcolor{red}{( \operatorname{sgn} \sigma )}\det(\boldsymbol{a_1}, \dots,\boldsymbol{a_n}).\end{aligned}

太字を行ベクトルとすると，

\begin{aligned}\det \begin{pmatrix}\boldsymbol{a_{\textcolor{red}{\sigma(1)}}} \\ \vdots \\ \boldsymbol{a_{\textcolor{red}{\sigma(n)}}} \end{pmatrix} = \textcolor{red}{(\operatorname{sgn} \sigma)} \det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_n}\end{pmatrix} .\end{aligned}

特に， 2つの列（または行）を入れ替えると，行列式は $\color{red} -1$ 倍になる。

4. 2つの列（または行）が等しい行列式の値は $\color{red} 0$ である。

5. 行列式と積は可換である。すなわち， $A,B$ を $n$ 次正方行列とするとき，

\color{red} \det (AB) = \det A \det B.

6. $A$ が正則のとき， $\color{red}\det (A^{-1}) = (\det A)^{-1} .$

今回はこの6つについて，証明付きで扱いましょう。

行列式の性質の証明

行列式の性質の前に，行列式の定義を復習しておきましょう。

行列式の定義

$n$ 次正方行列 $A =(a_{ij})$ に対し，

\color{red} \det A = \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}

を行列式 (determinant) という。

行列式の定義について詳しくは，行列式(det)の定義と現実的な求め方～計算の手順～を参照してください。

なお， $\sigma$ や $S_n$ は置換による記号です。これは，線形代数(行列)における置換・奇置換・偶置換の最低限必要な知識を参照してください。

1. 行列式の列・行の線形性

1. 行列式は，各列に関して線形性がある。すなわち， $\boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n$ を $n$ 次元列ベクトル， $s,t\in \mathbb{C}$ とすると，
$\small \begin{aligned}&\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{s\boldsymbol{a_k}+t\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\={}&\textcolor{red}{s} \det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{a_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}) \\ &+ \textcolor{red}{t}\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_{k-1}}, \textcolor{red}{\boldsymbol{b_k}}, \boldsymbol{a_{k+1}},\dots, \boldsymbol{a_n}).\end{aligned}$

また同様に，行列式は各行に関して線形性がある。すなわち， $\boldsymbol{a_k} \in \mathbb{C}^n \,\,(1\le k\le n), \,\, \boldsymbol{b_k} \in \mathbb{C}^n$ を $n$ 次元行ベクトル， $s,t\in \mathbb{C}$ とすると，
$\small \begin{aligned} &\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{s\boldsymbol{a_k} +t\boldsymbol{b_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} \\ &= \textcolor{red}{s}\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{\boldsymbol{a_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} +\textcolor{red}{t}\det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_{k-1}} \\ \textcolor{red}{\boldsymbol{b_k}} \\ \boldsymbol{a_{k+1}} \\ \vdots \\ \boldsymbol{a_n} \end{pmatrix} .\end{aligned}$

証明

列に関する線形性について

\boldsymbol{a_k} = \begin{pmatrix} a_{1k}\\ a_{2k}\\ \vdots \\ a_{nk} \end{pmatrix}

と定めると，積の分配法則により，

\begin{aligned}&\det (\boldsymbol{a_1}, \dots , s\boldsymbol{a_k}+t\boldsymbol{b_k}, \dots,\boldsymbol{a_n}) \\ &= \sum_{\sigma\in S_n}a_{1\sigma(1)}\dots (sa_{k\sigma(k)}+tb_{k\sigma(k)})\dots a_{n\sigma(n)} \\ &=s\sum_{\sigma\in S_n}a_{1\sigma(1)}\dots a_{k\sigma(k)}\dots a_{n\sigma(n)} \\ &\quad + t\sum_{\sigma\in S_n}a_{1\sigma(1)}\dots b_{k\sigma(k)}\dots a_{n\sigma(n)}\\ &=s\det (\boldsymbol{a_1}, \dots , \boldsymbol{a_k}, \dots ,\boldsymbol{a_n}) \\ &\quad+ t\det (\boldsymbol{a_1}, \dots , \boldsymbol{b_k}, \dots, \boldsymbol{a_n}) \end{aligned}

であるから，結論を得る。

行に関する線形性について

次の転置行列に関する性質2を用いて，列に関する線形性に帰着させればよい。

証明終

2. 転置行列の行列式は一致する

2. 転置行列の行列式は元のそれと同じ。すなわち， $\color{red}\det A = \det A^\top.$

証明

\begin{aligned} \det A &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{1\sigma(1)}a_{2\sigma(2)}\dots a_{n\sigma(n)}, \\ \det A^\top &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{\sigma(1)1}a_{\sigma(2)2}\dots a_{\sigma(n)n}\\ \end{aligned}

である。ここで，第2式の右辺を，最初の添え字に対して昇順に並び替えると，

\begin{aligned} &a_{\sigma(1)1}a_{\sigma(2)2}\dots a_{\sigma(n)n} \\ &= a_{1\sigma^{-1}(1)} a_{2\sigma^{-1}(2)}\dots a_{n\sigma^{-1}(n)} \end{aligned}

であることが分かる。 $\operatorname{sgn} \sigma = \operatorname{sgn} \sigma^{-1}$ であるから，結局，

\begin{aligned}&\det A^\top \\ &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma) a_{\sigma(1)1}a_{\sigma(2)2}\dots a_{\sigma(n)n}\\ &= \sum_{\sigma\in S_n} (\operatorname{sgn}\sigma^{-1} )a_{1\sigma^{-1}(1)} a_{2\sigma^{-1}(2)}\dots a_{n\sigma^{-1}(n)} \\ &= \sum_{\sigma^{-1} \in S_n} (\operatorname{sgn}\sigma^{-1} )a_{1\sigma^{-1}(1)} a_{2\sigma^{-1}(2)}\dots a_{n\sigma^{-1}(n)} \\ &= \det A \end{aligned}

となって $\det A^\top = \det A.$

証明終

3. 列・行の入れ替えと行列式

3. （列・行の入れ替え） $\sigma\in S_n$ を置換とする。このとき，太字を列ベクトルとすると，
$\begin{aligned}& \det(\boldsymbol{a_{\textcolor{red}{\sigma(1)}}}, \dots ,\boldsymbol{a_{\textcolor{red}{\sigma(n)}}})\\& =\textcolor{red}{( \operatorname{sgn} \sigma )}\det(\boldsymbol{a_1}, \dots,\boldsymbol{a_n}).\end{aligned}$

太字を行ベクトルとすると，
$\begin{aligned}\det \begin{pmatrix}\boldsymbol{a_{\textcolor{red}{\sigma(1)}}} \\ \vdots \\ \boldsymbol{a_{\textcolor{red}{\sigma(n)}}} \end{pmatrix}= \textcolor{red}{(\operatorname{sgn} \sigma)} \det \begin{pmatrix} \boldsymbol{a_1} \\ \vdots \\ \boldsymbol{a_n}\end{pmatrix} .\end{aligned}$

特に， 2つの列（または行）を入れ替えると，行列式は $\color{red} -1$ 倍になる。

証明

行に関する置換は，転置すること(性質2)で列に関する置換に帰着されるから，列の方のみ示そう。

\boldsymbol{a_k} = \begin{pmatrix} a_{1k}\\ a_{2k}\\ \vdots \\ a_{nk} \end{pmatrix}

と定めると，

\begin{aligned} &\det(\boldsymbol{a_{\sigma(1)}}, \dots ,\boldsymbol{a_{\sigma(n)}}) \\ &=\sum_{\tau\in S_n} (\operatorname{sgn}\tau) a_{\sigma(1)\tau(1)}a_{\sigma(2)\tau(2)}\dots a_{\sigma(n)\tau(n)} \\ &= \sum_{\tau\in S_n} (\operatorname{sgn}\tau) a_{1\sigma^{-1}\tau(1)}a_{2\sigma^{-1}\tau(2)}\dots a_{n\sigma^{-1}\tau(n)} \\ &= (\operatorname{sgn}\sigma)\sum_{\tau\in S_n} (\operatorname{sgn}\sigma^{-1}\tau) a_{1\sigma^{-1}\tau(1)}\dots a_{n\sigma^{-1}\tau(n)} \\ &= (\operatorname{sgn}\sigma)\det(\boldsymbol{a_1}, \dots,\boldsymbol{a_n}) \end{aligned}

より結論を得る。

証明終

4. 2つの列（または行）が等しい行列の行列式は0

4. 2つの列（または行）が等しい行列式の値は $\color{red} 0$ である。

これは性質3を使って証明されます。

証明

元の行列の行列式を $a$ とする。性質3の「2つの列（または行）を入れ替えると，行列式は $-1$ 倍になる」という性質から，等しい2列（または2行）を入れ替えても行列式は $-1$ になるはずである。従って，

a = -a

より， $a=0$ を得る。

証明終

5. 行列式と積は可換（det AB = det A det B)

5. 行列式と積は可換である。すなわち， $\color{red} \det (AB) = \det A \det B.$

証明

列ベクトルを用いて， $A = (\boldsymbol{a_1},\dots, \boldsymbol{a_n} ) = (a_{ij}), \,B= (b_{ij})$ とすると，

\begin{aligned} AB &= \left(\sum_{i_1=1}^n \boldsymbol{a_{i_1}}b_{i_1 1}, \dots, \sum_{i_n=1}^n \boldsymbol{a_{i_n}}b_{i_n n}\right) \end{aligned}

である。これと，性質1の線形性により，

\begin{aligned} &\det (AB) \\ &= \sum_{i_1=1}^n \dots \sum_{i_n=1}^n b_{i_11}\dots b_{i_nn}\det(\boldsymbol{a_{i_1}},\dots,\boldsymbol{a_{i_n}}).\end{aligned}

ここで，同じ列が2列以上ある行列式の値は $0$ である(性質4)から，

\small \begin{aligned}& \sum_{i_1=1}^n \dots \sum_{i_n=1}^n b_{i_11}\dots b_{i_nn}\det(\boldsymbol{a_{i_1}},\dots,\boldsymbol{a_{i_n}}) \\ &= \sum_{\sigma\in S_n} b_{\sigma(1)1}\dots b_{\sigma(n)n}\det(\boldsymbol{a_{\sigma(1)}},\dots,\boldsymbol{a_{\sigma(n)}}) \\ &= \sum_{\sigma\in S_n} b_{\sigma(1)1}\dots b_{\sigma(n)n}\{(\operatorname{sgn} \sigma)\det(\boldsymbol{a_1},\dots,\boldsymbol{a_n}) \} \\ &= \sum_{\sigma\in S_n}(\operatorname{sgn} \sigma) b_{\sigma(1)1}\dots b_{\sigma(n)n} \det A \\ &= \det B^\top \det A = \det A \det B. \end{aligned}

ただし，2つ目の等式は列の置換の性質3を，最後の等式は転置行列の行列式の性質2を用いた。

証明終

6. det (A^{-1}) = (det A)^{-1}

6. $A$ が正則のとき， $\color{red} \det (A^{-1}) = (\det A)^{-1} .$

証明

性質5より， $I$ を同じ大きさの単位行列とすると，

1 = \det I = \det (AA^{-1}) = \det A \det (A^{-1}) .

従って， $\det (A^{-1}) = (\det A)^{-1} .$

証明終

行列の基本変形による行列式の変化

上のことを踏まえて，行列の基本変形とそれによる行列式の変化について考えましょう。行列の基本変形によって，行列式は以下のように変化します。

基本変形	行列式	証明方法
ある行（列）の ${c}$ 倍を他の行（列）に加える	変化なし	行列式の線形性(性質1) と同じ列を持つ行列式は $0$ (性質4)から
2つの行（列）を入れ替える	$\boldsymbol{-1}$ 倍	列・行の置換の性質(性質3)から
ある行（列）を ${ c \ne 0 }$ 倍する	$\boldsymbol{ c}$ 倍	行列式の定義から明らか