積分を勉強するときに出てくる2つの言葉である「原始関数」と「不定積分」について,その専門数学における厳密な定義と違いについて述べ,理解を深めましょう。
原始関数・不定積分の厳密な定義
簡単のため,関数の定義域は実数全体 \mathbb{R} としますが,一部の区間であっても構いません。
原始関数の厳密な定義
まずは,原始関数の定義です。
定義(原始関数)
微分して f(x) になる関数 F(x) ,すなわち,
\color{red}F'(x) = f(x),\quad x\in \mathbb{R}
となるとき, F は f の原始関数 (primitive function) という。原始関数は, \displaystyle\color{red} \int f(x)\, dx とかくことがある。
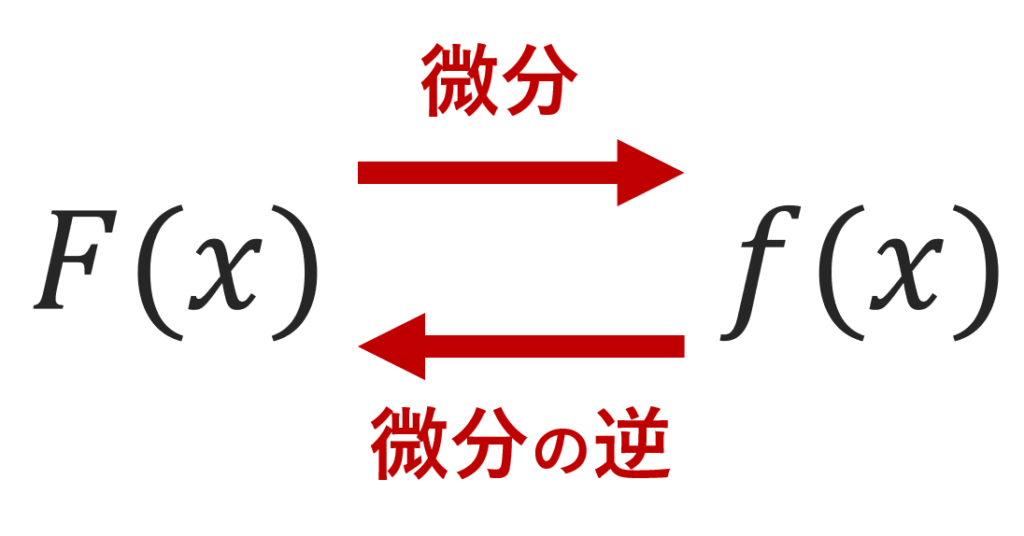
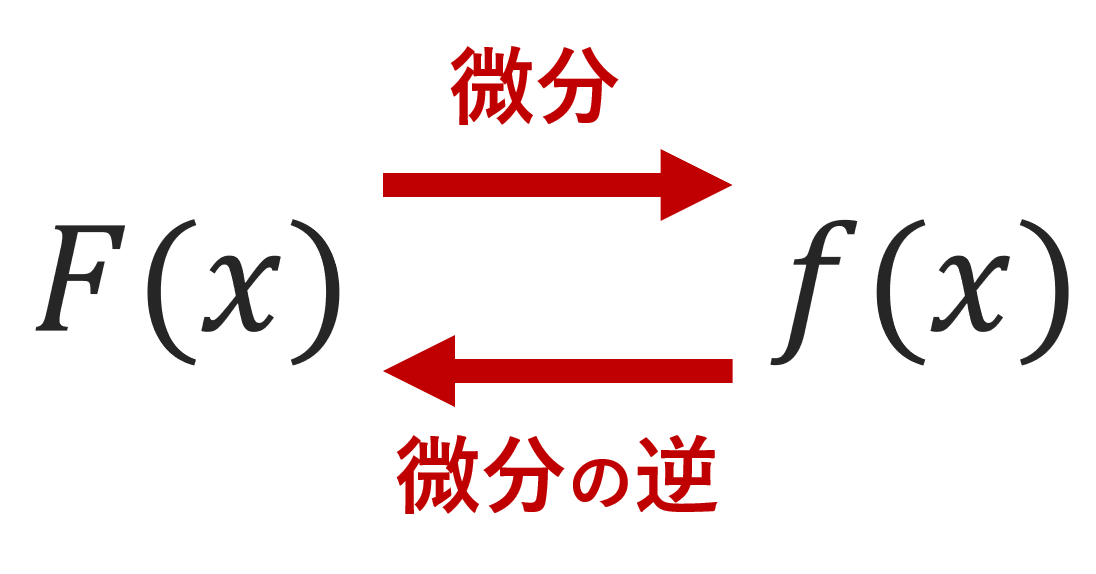
原始関数とは,微分の逆を指します。よって,微分の逆の操作を行うことで,原始関数を求めることができます。
原始関数は一つではありません。 F(x) を f(x) の原始関数としたとき, F(x) + C も f(x) の原始関数です。
たとえば, x^2 の原始関数は x^3/3 +C になります。このときの C は,積分定数などと呼ばれます。
不定積分の厳密な定義
つづいて,不定積分を定義しましょう。不定積分を理解するには,まずは定積分 \int_a^bf(x)\, dx を理解せねばなりません。不定積分は,定積分から定義されるのです。
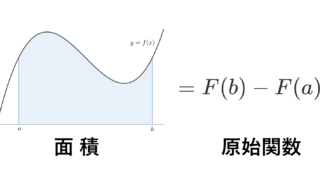
定積分は,面積として定義されます。以下の図を見てください。
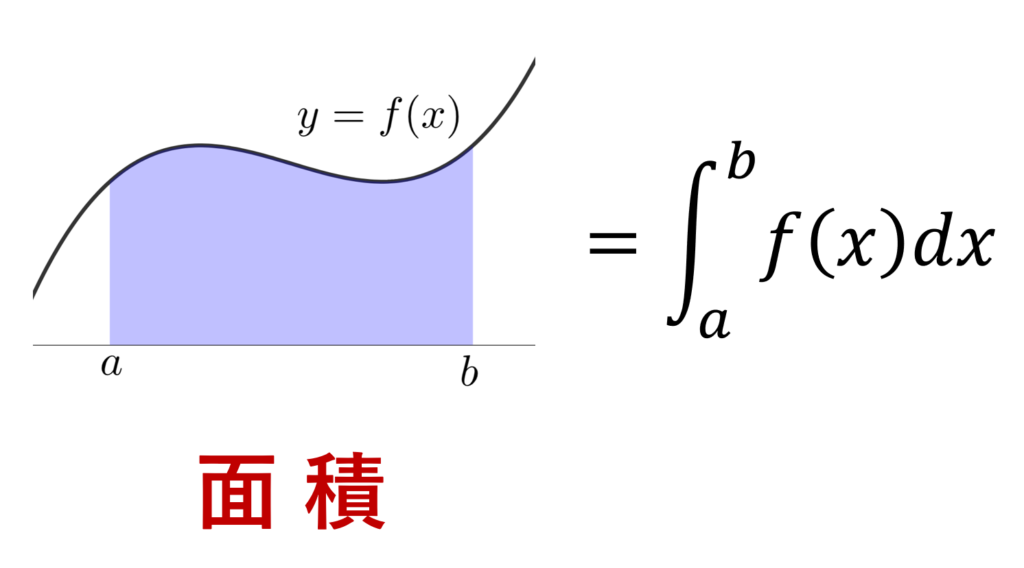
このように,関数に対し,それと x 軸との間の面積を定積分(リーマン積分)とします。詳しくは,リーマン和による定積分の定義とリーマン積分可能・不可能な例を確認してください。
この定積分に対し,面積を考える区間に変数 x を導入し,インテグラルの部分を x に関する関数とみたものが不定積分です。定義を述べましょう。
定義(不定積分)
a\in \mathbb{R} とし, f を閉区間上積分可能であるとする。このとき,
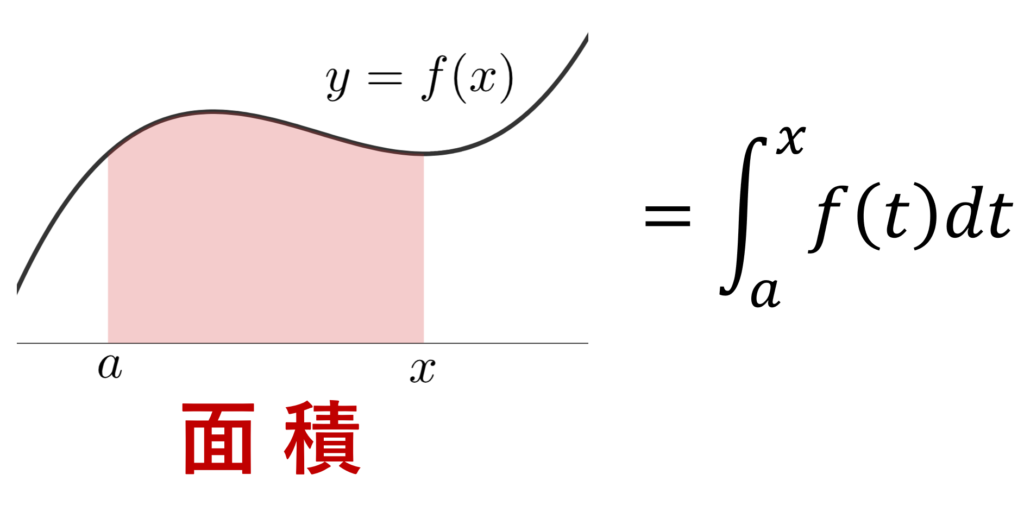
\color{red} \mathcal{F}(x) = \int_a^x f(t)\, dt,\quad x\in \mathbb{R}
を f の不定積分 (indefinite integral) という。
最初に注意として述べましたが,高校では,「不定積分」は「原始関数」であると定義します。よって,不定積分と原始関数の定義は全く同じになります。今は,そういう立場で話をしていないという点を留意してください。
原始関数・不定積分の違い
両者の違いを表にまとめておきましょう。
| 原始関数 | 不定積分 |
|---|---|
| F'(x) = f(x) となる F | \mathcal{F}(x) = \int_a^x f(t)\, dt となる \mathcal{F} |
| 微分の逆 | 面積を求める「定積分」を「変数化」 |
原始関数・不定積分の具体例
原始関数は存在しないが,不定積分は存在する例を述べます。
例
f(x) =\begin{cases}0 & x=0, \\ 1 & x\ne 0 \end{cases} とおくと,f の原始関数は存在しないが,不定積分は存在する。
f のように,1点だけで微分が 0 ,残りで微分が 1 になるような原始関数は存在しませんが,一方で,1点だけ 0 であっても,面積には影響を与えないため,不定積分は存在するというわけです。
原始関数と不定積分の両方が存在すればある意味一致する
ある関数 f について,原始関数と不定積分の両方が存在するとき,
\int_a^x f(t)\, dt = F(x)-F(a)
の関係があることが知られています。これを,微分積分学の基本定理といいます。これは,以下で証明しています。
原始関数は「微分の逆」で,不定積分は「面積」でしたから,「微分の逆」と「面積」が同じものである,といっているわけで,大変重要な定理です。この定理があるからこそ,面積を求めるのに,原始関数を経由して求めることができるというわけですね。
高校では,原始関数と不定積分はあまり区別しませんが,結局両方一致しているので,区別しなくても差し支えない,ということですね。