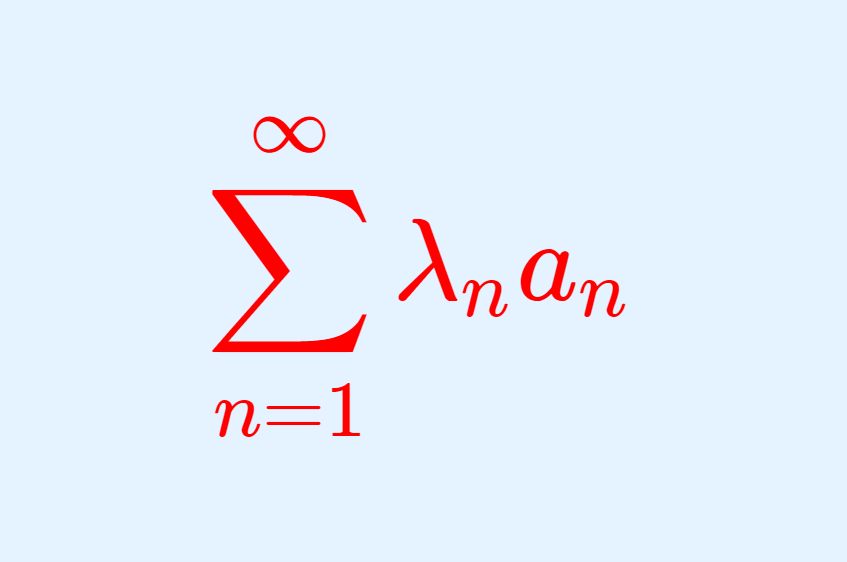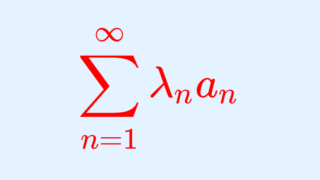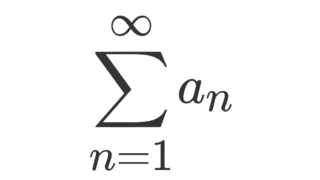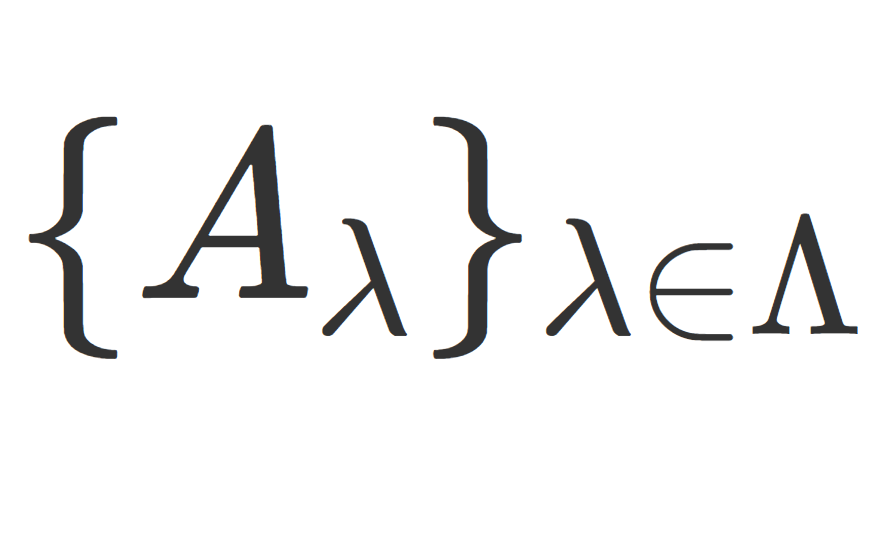アーベルの収束判定法と呼ばれる収束判定法について,その主張と証明を紹介しましょう。
アーベルの収束判定法
定理(アーベルの収束判定法; Abel’s test)
\{\lambda_n\} は単調かつ有界列とし,\sum_{n=1}^\infty a_n は収束(絶対収束または条件収束)するとする。このとき,
\large \color{red} \sum_{n=1}^\infty \lambda_n a_n
は収束する。
早速証明を考えていきましょう。
アーベルの収束判定法の証明
定理の証明のために,以下の補題を用います。
数列 \{a_n\}, \{b_n\} に対し,A_n = \sum_{k=1}^n a_k, B_n = \sum_{k=1}^n b_k とおく。このとき,
\color{red} \sum_{k=1}^n a_n b_n = a_n B_n - \sum_{k=1}^{n-1} (a_{k+1}- a_k) B_k
が成立する。
これは,部分積分 \int fg = fG- \int f' G の離散版だと思えます。証明は,以下の記事の途中で解説しています。
これを用いて,定理の証明を行いましょう。
定理の証明
\{\lambda_n\} が単調増加として示すことにする。
S_n=\sum_{k=1}^n a_k,\; S=\lim_{n\to\infty}S_n とおく。 \{S_n\} は収束するため有界である(→収束する数列は有界であることの証明)。よって, |S_n|\le M としよう。
また,\{\lambda_n\} は有界かつ単調増加なので,収束する(→上に有界な単調増加数列は収束することの証明)。よって, \lambda_n\xrightarrow{n\to\infty} \lambda としよう。
部分和分の公式より,
\!\!\!\!\sum_{k=1}^n \lambda_n a_n = \lambda_n S_n - \sum_{k=1}^{n-1} (\lambda_{k+1}- \lambda_k) S_k. \tag{1}
右辺について,第一項は \lambda_nS_n \xrightarrow{n\to\infty} \lambda S であり,第二項については, \lambda_{k+1}\ge \lambda_{k} であるから,
なので,絶対収束する。したがって, (1) 式の右辺が収束するため,左辺も収束する。
証明終
無事証明できましたね。