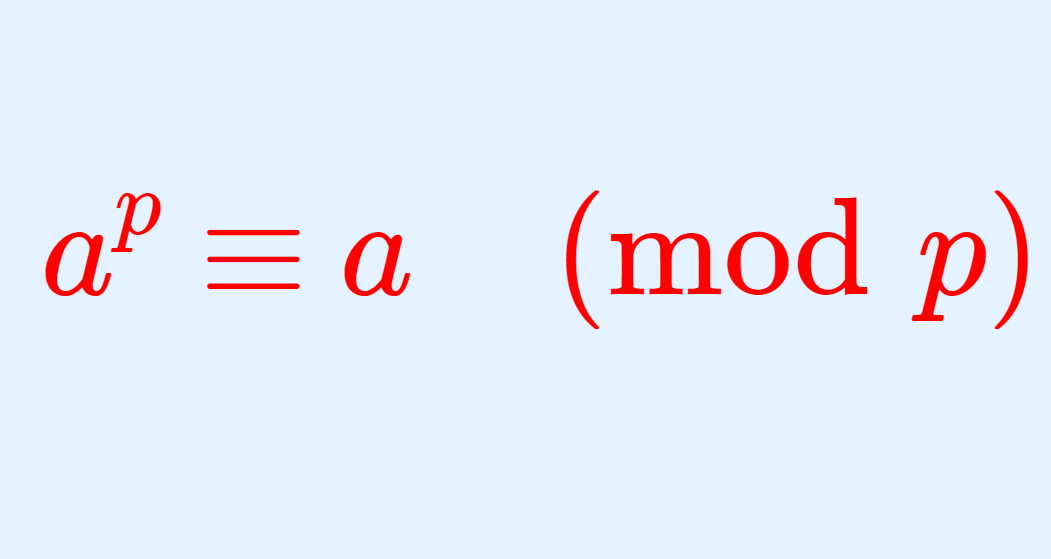「代数的数」とは,有理数係数の(多項式)= 0 の解になり得る複素数を指し,「超越数」とは,そうでない複素数を指します。これについて,定義・例と基本的な性質を紹介します。
超越数・代数的数とは
定義(超越数・代数的数)
0 でない有理数係数の多項式の根,すなわち, 0=0 の形でない方程式
\begin{aligned}a_nx^n+a_{n-1}x^{n-1}+\dots + a_1x+a_0=0 \qquad \\ a_n, a_{n-1},\dots, a_1,a_0\in\mathbb{Q},\, n\ge 1 \end{aligned}
の解になり得る複素数 x\in\mathbb{C} を代数的数 (algebraic number) という。代数的数でない複素数を超越数 (transcendental number) という。
代数的数全体の集合は \color{red} \overline{\mathbb{Q}} とかくことが多い。
代数的数を \overline{\mathbb{Q}} とかくのは,これは代数的な意味で \mathbb{Q} の「閉包」になっているからです。位相的な意味では, \mathbb{Q} の閉包は \mathbb{R} です。
なお,代数的数のうち,実数で無理数のものを代数的無理数といいます。
具体例を見ていきましょう。
超越数・代数的数の例
代数的数の例
- \mathbb{Q}(有理数)
- \sqrt[n]{q} \quad (q\in\mathbb{Q},\, n\in\mathbb{Z}_{\ge 2})
1. については, q\in\mathbb{Q} は x-q=0 の解ですから,代数的数で,2. については, x^n-q=0 の解ですから,代数的数ですね。2.については, q<0 でも可ですから,虚数にもなり得ることに注意してください。
なお,5次以上の多項式の根は四則演算とべき根の組み合わせでは書けないことが知られていますから,代数的数だからと言って,四則演算とべき根でかける,なんてことはありません。
超越数の例
- \pi(円周率)
- e(ネイピア数)
- 2^{\sqrt{2}}
超越数であることの証明は難しく,たとえば \pi+e が超越数になるかどうかは分かっていません。
超越数・代数的数の基本的な性質
代数的数と超越数の基本的な性質を順に紹介しましょう。
代数的数の性質
定理(代数的数の性質)
\overline{\mathbb{Q}} を代数的数全体の集合とする。
1.の,代数的数が可算集合である証明については,以下の記事の「可算集合の具体例」のところで証明しています。
超越数の性質
定理(超越数の性質)
\mathbb{C}\setminus\overline{\mathbb{Q}} を超越数全体の集合とする。
- \mathbb{C}\setminus\overline{\mathbb{Q}} は連続体濃度を持つ。
これは, \mathbb{C} が連続体濃度であることと, \mathbb{Q} が可算濃度であることから,従いますね。
なお,この定理は,代数的数より超越数の方がはるかに多く,複素数のほとんどが超越数であることを言っています。