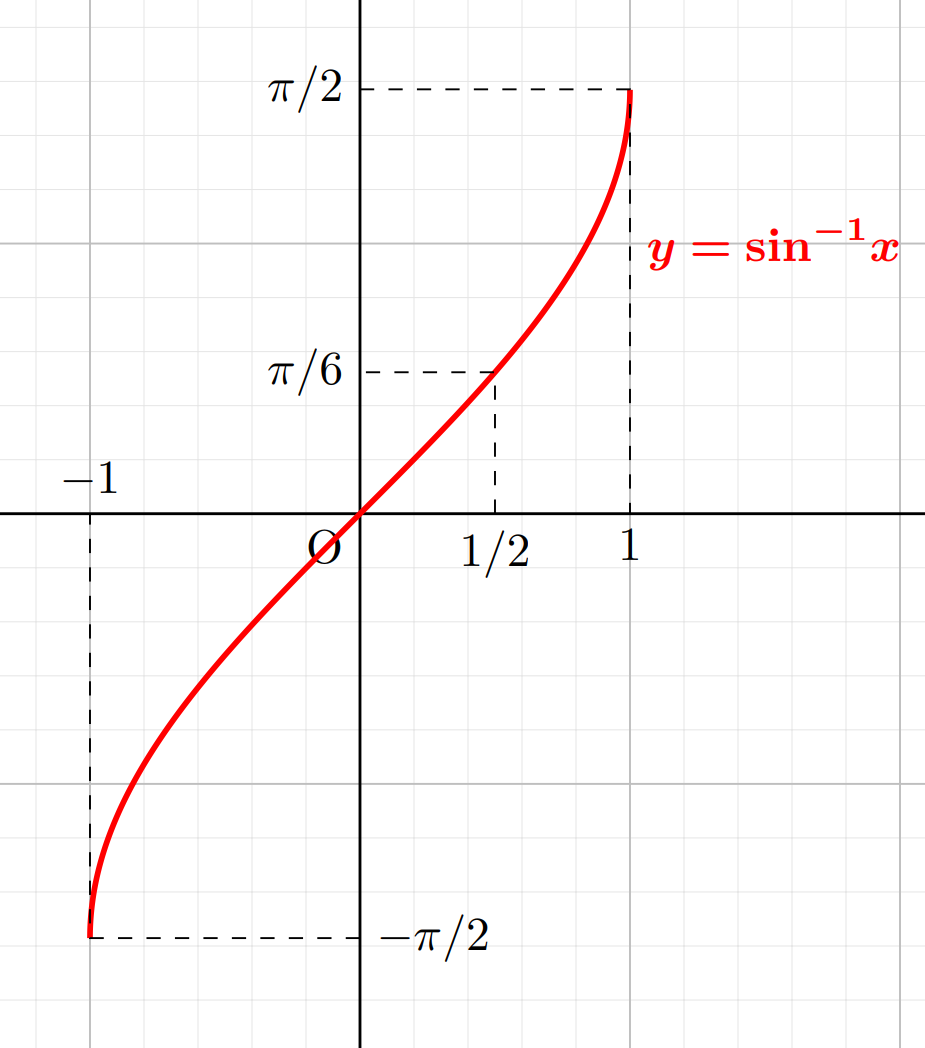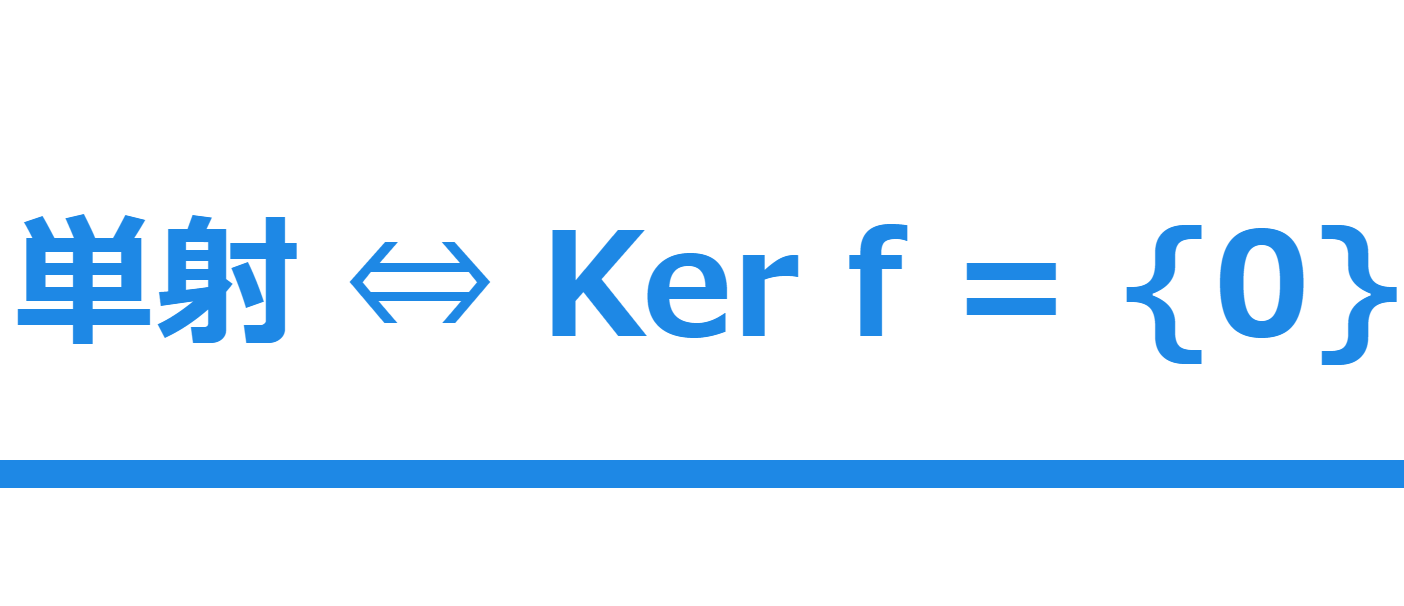三角関数の逆関数について,定義とそのグラフ,性質をまとめます。
逆三角関数の定義
\sin \colon \mathbb{R} \to [-1,1] は単射でないため逆関数は定義できませんが,定義域を [-\pi/2, \pi/2] に制限すれば,これは全単射になり,逆関数が定義できます。
同様にして \cos, \tan の逆関数も,定義域を制限すれば考えられます。実際の定義を述べましょう。
定義(逆三角関数)
- \sin x \, (-\pi/2 \le x \le \pi/2) の逆関数を \color{red} \sin^{-1} x \, (-1\le x\le 1) や \color{red} \arcsin x などと書く。
- \cos x \, (0 \le x \le \pi) の逆関数を \color{red} \cos^{-1} x \, (-1\le x\le 1) や \color{red}\arccos x などと書く。
- \tan x \, (-\pi/2 < x < \pi/2) の逆関数を \color{red} \tan^{-1} x \, (-\infty< x < \infty) や \color{red} \arctan x などと書く。
このように,逆三角関数を(一価の)関数とみたときの取る値を主値といいます。定義域を主値を表でまとめましょう。
| 逆三角関数 | 定義域 | 主値 |
|---|---|---|
| \theta = \sin^{-1} x | -1 \le x \le 1 | -\pi/2 \le \theta \le \pi/2 |
| \theta = \cos^{-1} x | -1 \le x \le 1 | 0 \le \theta \le \pi |
| \theta = \tan^{-1} x | -\infty < x < \infty | -\pi/2 < \theta < \pi/2 |
逆三角関数のグラフ
3つのグラフを確認しておきましょう。
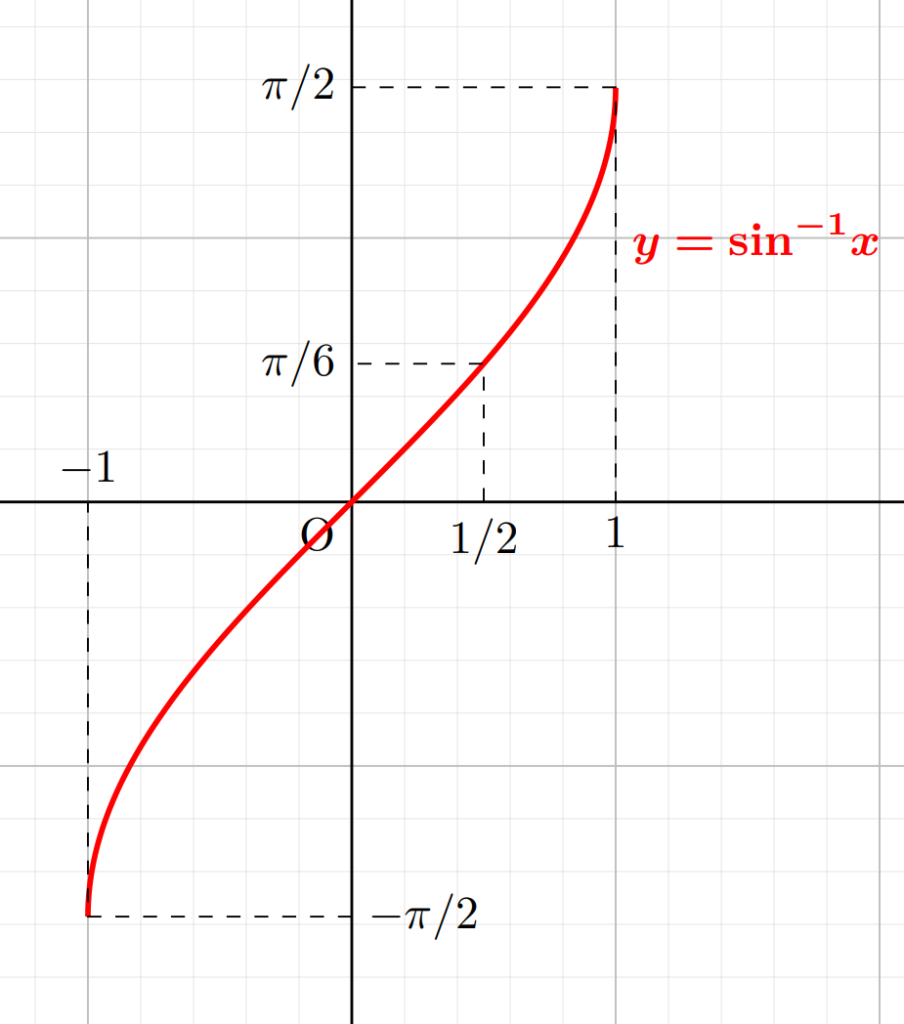
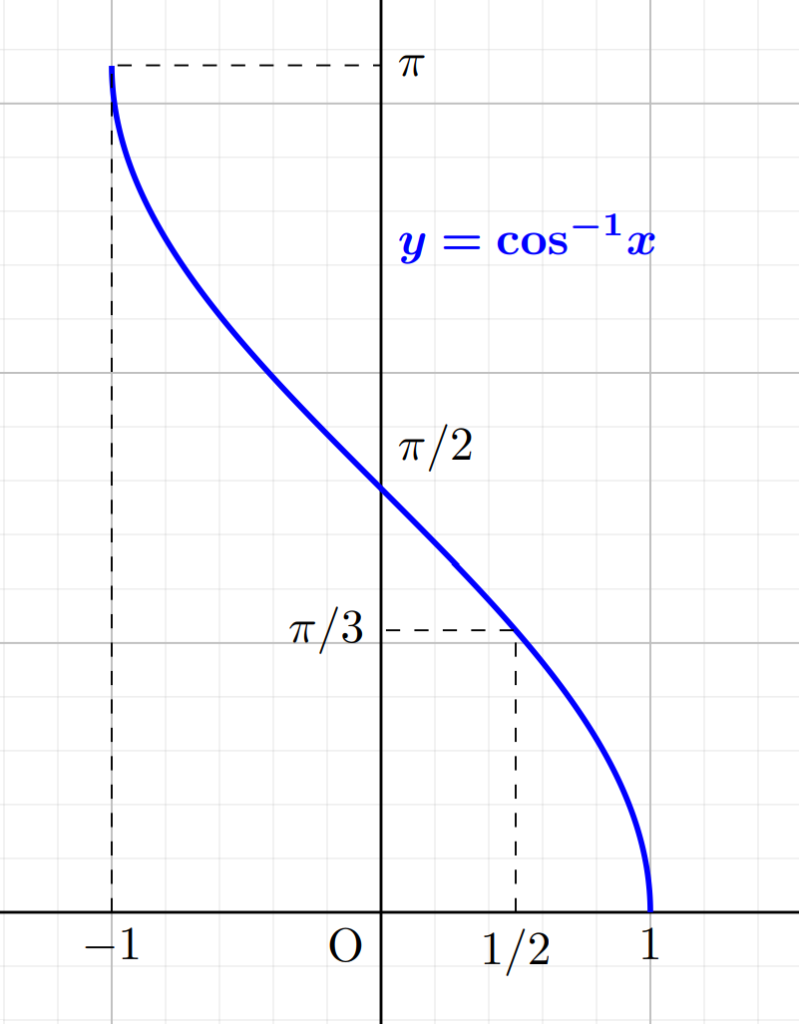
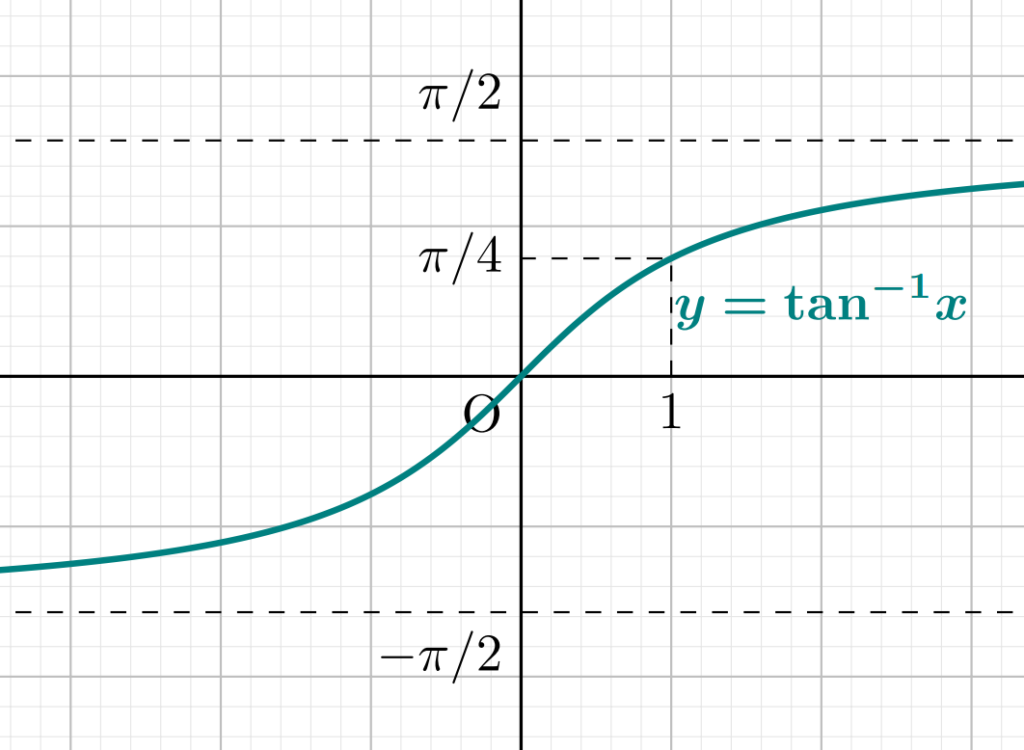
逆三角関数の性質
さまざまな性質をまとめてみましょう。
基本的な性質
定理(逆関数の基本的な性質)
- \sin^{-1} (-x) = - \sin^{-1} x, \,\, -1\le x\le 1.
- \cos^{-1} (-x) = \pi -\cos^{-1} x, \,\, -1\le x\le 1.
- \tan^{-1}(-x) = -\tan^{-1} x, \,\, x\in \mathbb{R}
- \cos (\sin^{-1} x) = \sin(\cos^{-1} x) = \sqrt{1-x^2},\,\, -1 \le x\le 1.
- \sin^{-1} x + \cos^{-1} x = \pi /2, \,\, -1 \le x \le 1.
- \tan^{-1} x + \tan^{-1} 1/x = \begin{cases} \pi/2 & x>0, \\ -\pi/2 & x< 0.\end{cases}
- \displaystyle \lim_{x\to 0} \frac{\sin^{-1}x}{x} = 1.
証明は,三角関数の基本的な性質(たとえば \sin x = \cos (\pi/2 -x ) など)を組み合わせればできます。
逆三角関数の微分
定理(逆三角関数の微分)
- \displaystyle(\sin^{-1} x)' = \frac{1}{\sqrt{1-x^2}}, \,\, -1<x<1.
- \displaystyle (\cos^{-1} x)' = -\frac{1}{\sqrt{1-x^2}}, \,\, -1<x<1.
- \displaystyle (\tan^{-1} x)' = \frac{1}{1+x^2}, \,\, x\in \mathbb{R}.
逆関数の微分法を用いれば証明可能です。
なお,これを逆に用いた「積分公式」は有名です。以下で述べましょう。
逆三角関数が出てくる積分
- \color{red} \displaystyle \int \frac{1}{\sqrt{a^2-x^2}}\, dx = \sin^{-1} \frac{x}{a} + C.
- \color{red}\displaystyle \int \frac{1}{a^2+x^2}\, dx = \frac{1}{a} \tan^{-1} \frac{x}{a} + C.
ただし, C は積分定数である。
逆三角関数の不定積分
定理(逆三角関数の不定積分)
- \displaystyle\int \sin^{-1} x \, dx = x \sin^{-1} x + \sqrt{1-x^2} + C.
- \displaystyle\int \cos^{-1} x \, dx = x\cos^{-1} x - \sqrt{1-x^2} + C.
- \displaystyle \int \tan^{-1} x \, dx = x \tan^{-1} x - \frac{\log (1+x^2)}{2} + C.
ただし, C は積分定数である。
このくらいの知識があれば,基本的な範囲で困ることは,おそらくないでしょう。