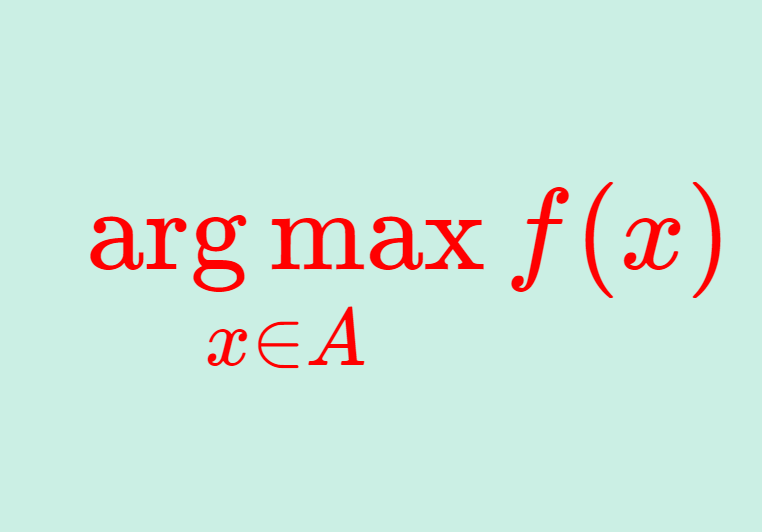応用数学でよく出てくる,argmax (最大点集合), argmin (最小点集合)の意味を具体例とともに説明します。
argmax, argminの定義
定義 (最大点集合; argment of the maximum・最小点集合; argument of the minimum)
集合 A 上 f(x) が最大となる x の集合を
\textcolor{red}{\argmax_{x\in A} f(x) = \{x\in A \mid f(x) = \max_{y\in A} f(y) \}}
とかき,集合 A 上 f(x) が最小となる x の集合を
とかく。ただし,\max_{y\in A} f(y),\min_{y\in A} f(y) が存在しないとき, \argmax, \argmin は空集合 \varnothing と考える。
なお, \max_{y\in A} f(y) は A 上の f(y) 最大値を指し, \min_{y\in A} f(y) は A 上の f(y) 最小値を指します。
最大値そのものを返すのが \textcolor{red}{\max} であり,最大値となる x の集合を返すのが \textcolor{red}{\argmax} です。
定義と同値な表現をいくつか与えておきましょう。
定義と同値な表現
- \displaystyle \argmax_{x\in A} f(x) = \{ x\in A \mid f(y) \le f(x) \text{ for each } y \in A \}
- \displaystyle \argmin_{x\in A} f(x) = \{ x\in A \mid f(x) \le f(y) \text{ for each } y \in A \}
- \displaystyle \argmax_{x\in A} f(x) = \{x\in A \mid f(x) = \sup_{y\in A} f(y) \}
- \displaystyle \argmin_{x\in A} f(x) = \{x\in A \mid f(x) = \inf_{y\in A} f(y) \}
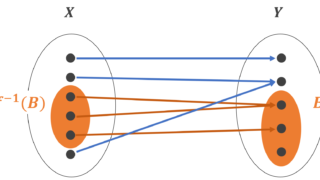
- \displaystyle \argmax_{x\in A} f(x) = f^{-1} (\max_{y\in A} f(y))
- \displaystyle \argmin_{x\in A} f(x) = f^{-1} (\min_{y\in A} f(y))
ただし,下2つの定義は \max_{y\in A} f(y), \min_{y\in A} f(y) が存在しないとき,空集合 \varnothing と考える。
ここで, f^{-1} は逆像を意味します。逆像については以下の記事を参照してください。
argmax, argminの具体例
具体例を挙げましょう。
例
- \displaystyle \max_{1\le x\le 3} x^2 = 9,
- \displaystyle\argmax_{1\le x\le 3} x^2 = \{3\}.
- \displaystyle\max_{x\in \mathbb{R}} \sin x = 1,
- \displaystyle\argmax_{x\in \mathbb{R}} \sin x = \{(\tfrac{1}{2}+ 2n )\pi\mid n\in\mathbb{Z}\}.
- \displaystyle \max_{x>0} \tfrac{1}{x}; 存在しない,
- \displaystyle \argmax_{x>0} \tfrac{1}{x} = \varnothing.
普段から使えるようにしていきましょう。