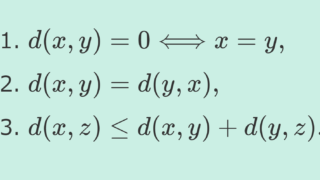バナッハの不動点定理 (Banach’s fixed-point theorem) あるいは縮小写像の原理 (contraction mapping principle) とは, 縮小写像 f\colon X\to X が唯一つ不動点を持ち,その不動点は任意の点から f で何回もうつすことで近似可能という定理です。
これについて,主張と証明を行いましょう。
バナッハの不動点定理(縮小写像の原理)
バナッハの不動点定理(縮小写像の原理)
(X,d) を空でない完備距離空間とし, 0<k<1 とする。 f\colon X\to X が任意の x,y\in X に対し,
\color{red}\begin{equation} \large d(f(x),f(y))\le kd(x,y)\end{equation}
をみたすとき, f(x^*) = x^* となる x^*\in X が唯一つ存在する。さらに,そのような x^* は任意の x \in X に対し,
となる。ただし, f^n= \underbrace{f\circ \dots \circ f}_{n} (n 回合成)を表す。
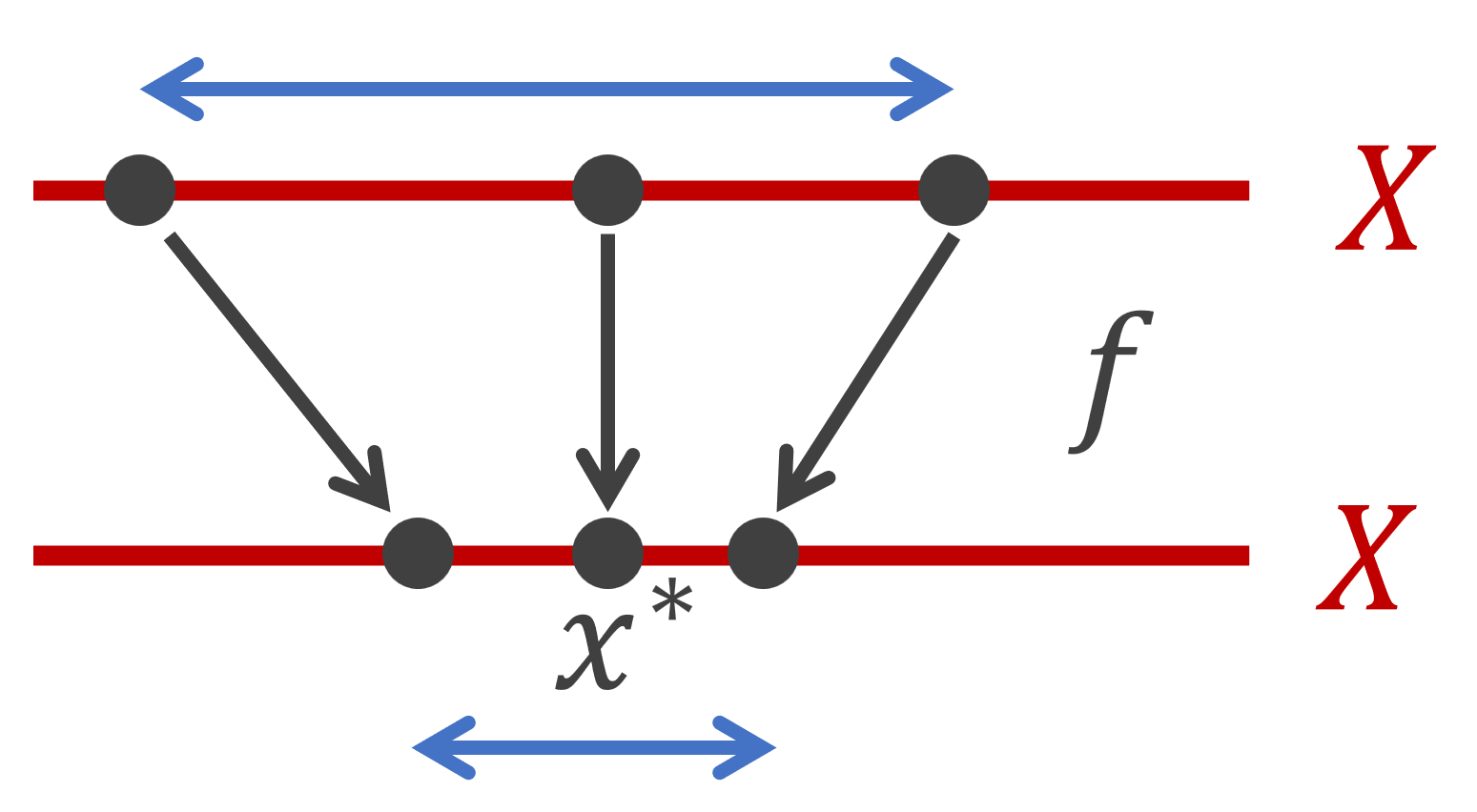
(1) 式をみたすような写像 f\colon X\to X を縮小写像 (contraction mapping) といいます。2点の距離は f でうつすことで必ず近づきます。縮小写像は定義からリプシッツ連続です。
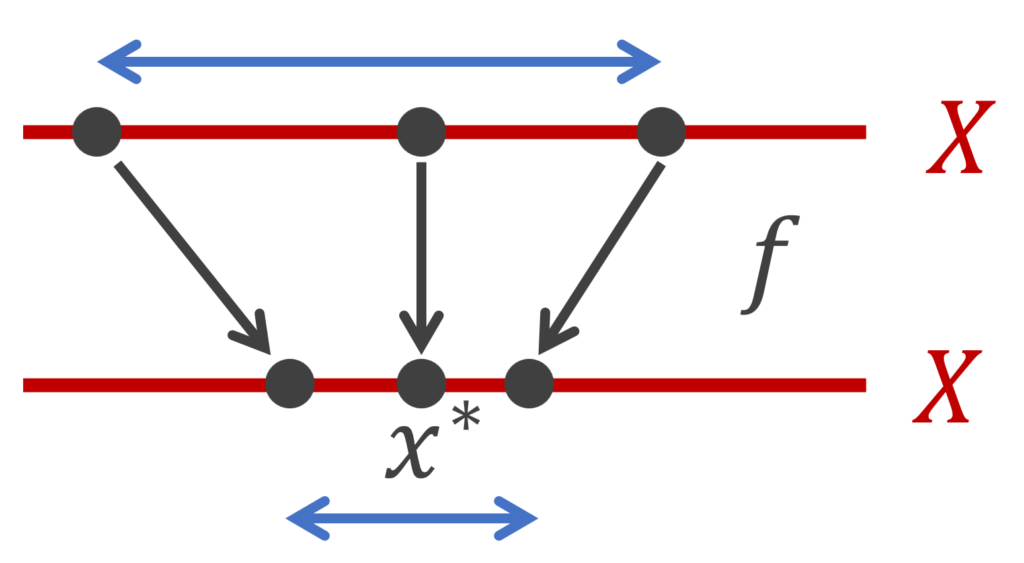
このような, f(x^*)=x^* をみたす点 x^* のことを不動点 (fixed point) といいます。本定理は,縮小写像には不動点が唯一つ存在する,と言っているわけですね。さらに,f で何回もうつすことで,任意の点から不動点に近づけることができるということです。
バナッハの不動点定理(縮小写像の原理)の証明
証明
x\in X とし,x_n=f^n(x) とする。まず, \{x_n\} が収束することを示そう。
0<m<n に対し,三角不等式より
\begin{aligned}&d(x_m,x_n) \le \sum_{i=m}^{n-1}\ d(x_i, x_{i+1}) \end{aligned}
である。ここで, f は縮小写像であったから,
となる。よって,
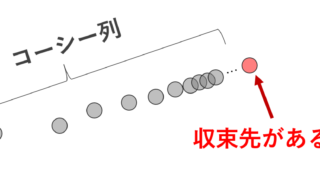
であり, \{x_n\} はコーシー列である。 X は完備であるから,収束先 x_n \xrightarrow{n\to\infty} x^*\in X が存在する。
次に, x^* が不動点であることを示す。 f は連続であるから,
\begin{aligned} f(x^*)&=f\left(\lim_{n\to\infty} x_n\right) = \lim_{n\to\infty}f(x_n)\\&=\lim_{n\to\infty}x_{n+1}=x^*\end{aligned}
であり, x^* は不動点である。最後に不動点が唯一つであることを示す。 x^*, x^{**}\in X を不動点とする。 f は縮小写像より,
であり, 0\le k<1 であったから, d(x^*, x^{**})=0 すなわち, x^*=x^{**} である。
証明終
本定理は,微分方程式の解の存在や,実際にその解の構成を行うのによく使われます。微分方程式の解の構成は x^*=\lim_{n\to\infty}f^n(x) を用いて行われますが,これを ピカールの逐次近似法 と言ったりします。
これについては,いずれ別の記事で解説しましょう。