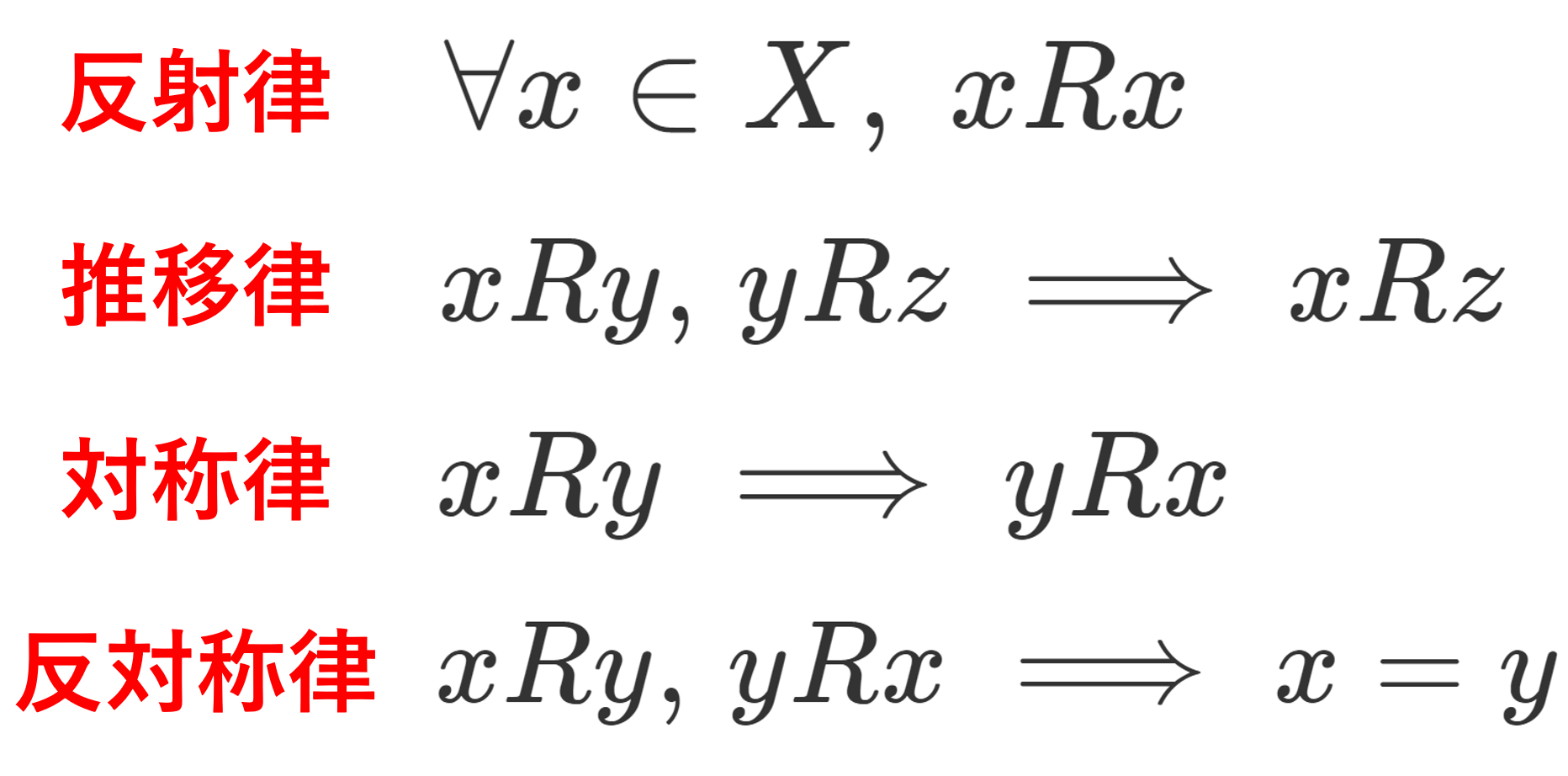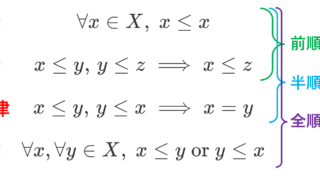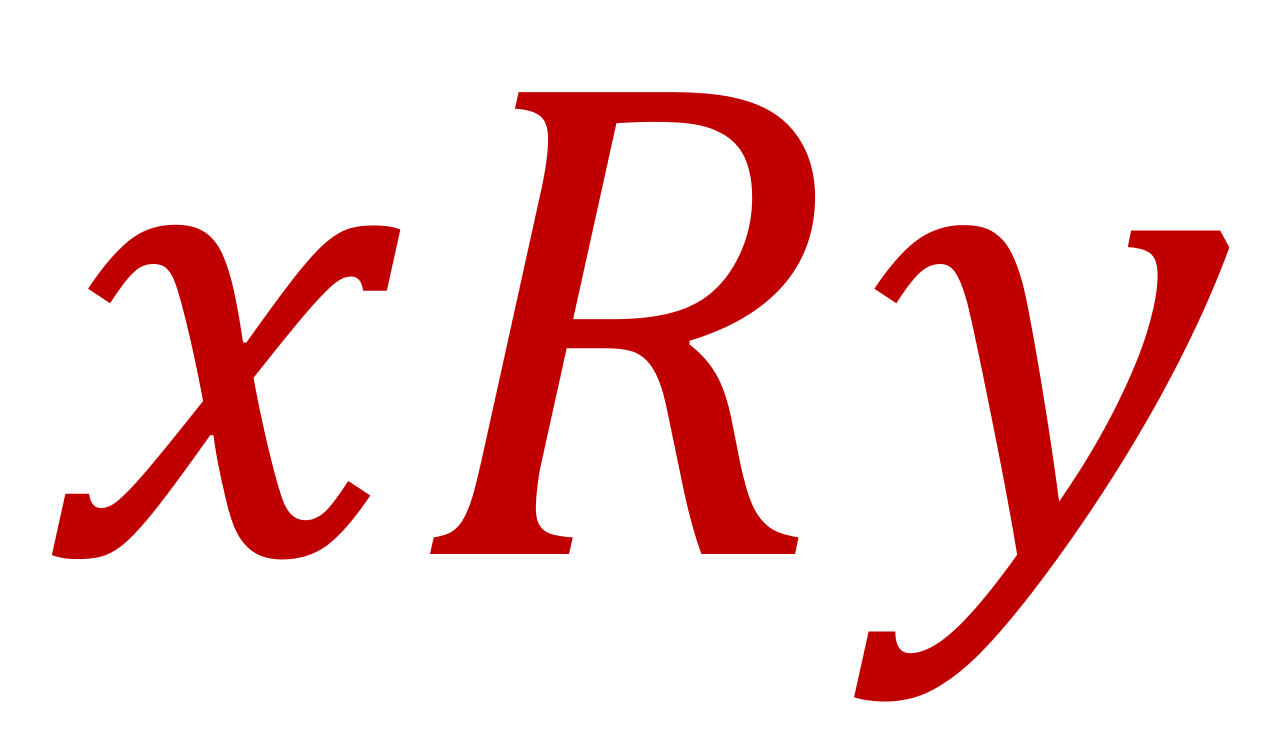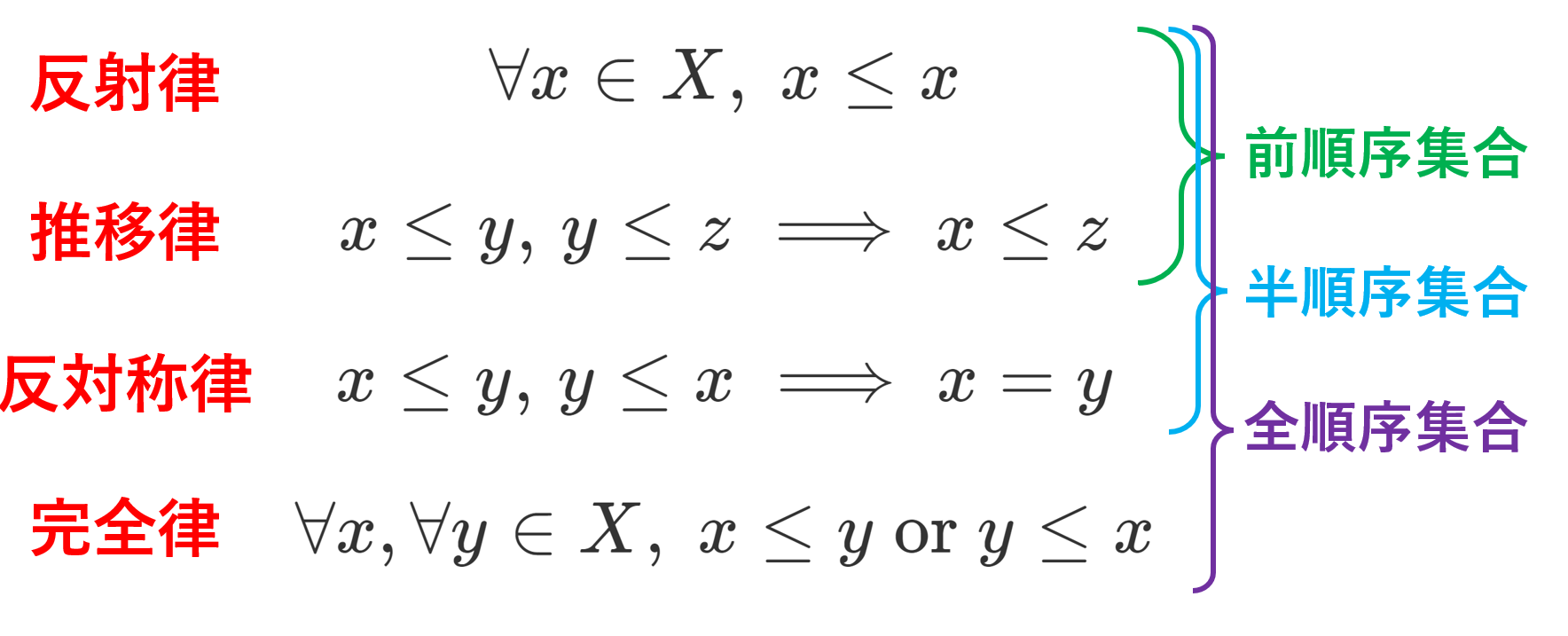二項関係の性質である,反射律・推移律・対称律・反対称律の定義と具体例7つを紹介します。
反射律・推移律・対称律・反対称律の定義
反射律・推移律・対称律・反対称律とは,集合上の二項関係 xRy に成り立つ性質を指します。定義を見ていきましょう。
定義(反射律・推移律・対称律・反対称律)
空でない集合 X 上の二項関係 R について,
- 任意の x\in X に対して, xRx が成り立つとき, R は反射律 (reflexive relation) をみたすという。
- x,y,z\in X が xRy,\; yRz を共にみたすとき,常に xRz もみたすなら, R は推移律 (transitive relation) をみたすという。
- x,y\in X が xRy をみたすとき,常に yRx もみたすなら, R は対称律 (symmetric relation) をみたすという。
- x,y\in X が xRy,\; yRx を共にみたすとき, x=y となるなら, R は反対称律 (antisymmetric relation) をみたすという。
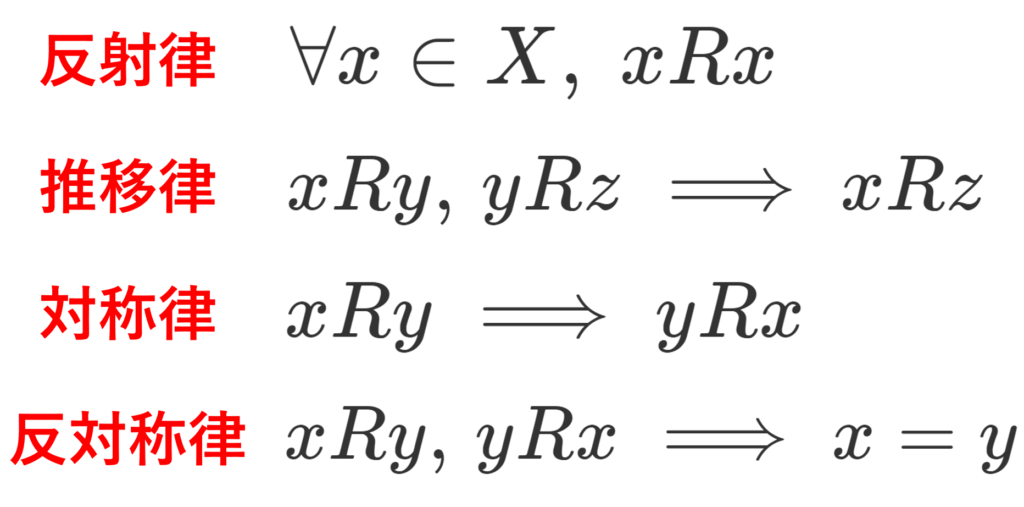
二項関係は R という記号を用いて,xRy とかきましたが,たとえば,順序関係(大小関係)には x\le y のように,\le を用いますし,他の記号を用いることもあります。
反射律・推移律・対称律・反対称律の具体例7つ
各二項関係について,それぞれ反射律・推移律・対称律・反対称律をみたすかを表にしました。
| 二項関係 | 反射律 | 推移律 | 対称律 | 反対称律 |
|---|---|---|---|---|
| = | 〇 | 〇 | 〇 | 〇 |
| \le on \mathbb{R} | 〇 | 〇 | × | 〇 |
| < on \mathbb{R} | × | 〇 | × | 〇 |
| \equiv \pmod p on \mathbb{Z} | 〇 | 〇 | 〇 | × |
| x R y \stackrel{\mathrm{def}}{\iff} |x-y|<1 on \mathbb{R} | 〇 | × | 〇 | × |
| xR y \stackrel{\mathrm{def}}{\iff} y=2x on \mathbb{R} | × | × | × | 〇 |
| 1R1,\, 2R2,\, 1R2, \,2R1 であるが, これ以外に二項関係がない on \mathbb{R} | × | 〇 | 〇 | × |
たとえば, \le は 1\le 2 ですが, 2\le 1 は不成立のため,対称律をみたしません。一方で, x\le y,\, y\le x\implies x=y なので,反対称律は成立します。
< については, x<x が成立しないため,反射律は成り立ちません。反対称律については,そもそも x<y,\, y<x を同時に満たす x,y が存在しないため, x<y,\, y<x \implies x=y は真になります。
これは, P\implies Q は,P が偽なら,真となるからです。
残りのチェックは,演習問題としましょう。
同値関係と順序関係
二項関係のうち,反射律・推移律・対称律をみたすものを同値関係 (equivalence relation),反射律・推移律・反対称律をみたすものを(半)順序関係 (partially ordered relation) といいます。これらは,数学においてよく考えられる二項関係です。
| 二項関係の名前 | 反射律 | 推移律 | 対称律 | 反対称律 |
|---|---|---|---|---|
| 同値関係 \sim (例: \equiv \pmod p on \mathbb{Z} ) | 〇 | 〇 | 〇 | |
| (半)順序関係 \le (例: \le ) | 〇 | 〇 | 〇 |
これらについては,以下で詳しく解説することにしましょう。