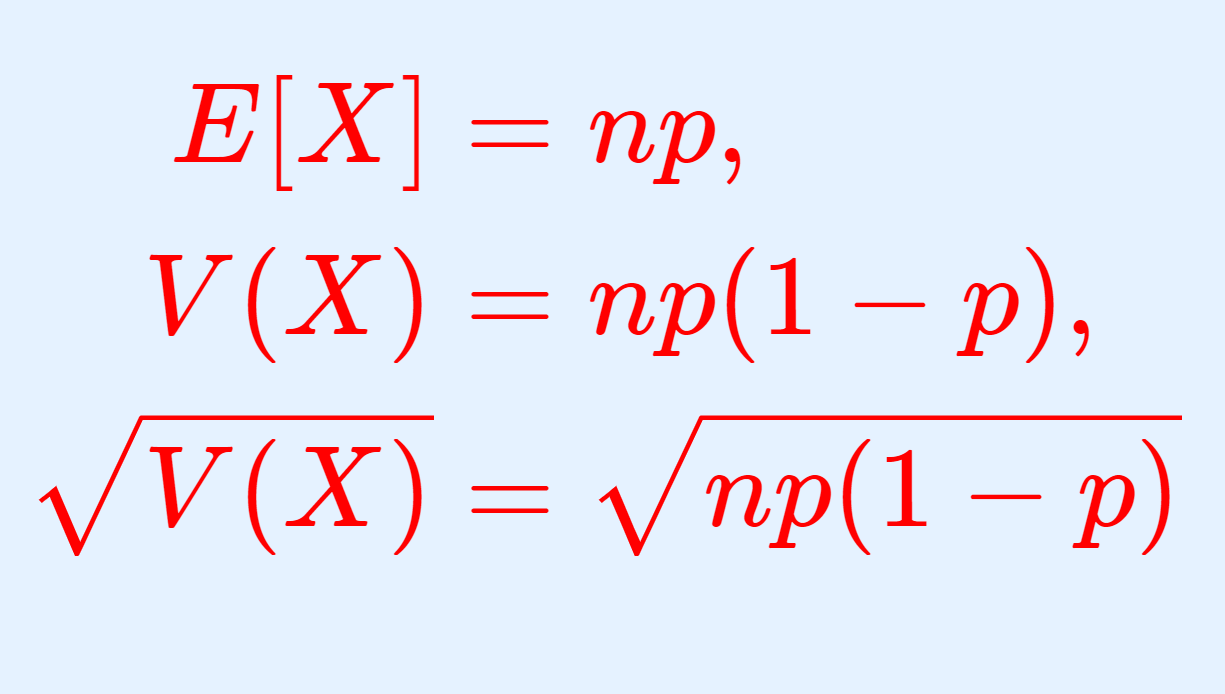有名な確率分布の1つである,「二項分布」について,その期待値(平均)・分散・標準偏差は
\begin{aligned} E[X]&= np, \\ V(X)&= np(1-p), \\ \sqrt{V(X)} &= \sqrt{np(1-p) } \end{aligned}となります。この証明を,「定義から直接証明」「ベルヌーイ分布の和を用いた証明」「特性関数の微分を用いた証明」の3通りで行います。
二項分布の期待値(平均)・分散・標準偏差
もう一度,期待値・分散・標準偏差をまとめましょう。
定理(二項分布の期待値・分散・標準偏差)
X\sim B(n,p) であるとき, X の期待値・分散・標準偏差はそれぞれ
\color{red}\begin{aligned} E[X]&= np, \\ V(X)&= np(1-p), \\ \sqrt{V(X)} &= \sqrt{np(1-p) } \end{aligned}
となる。
二項分布の期待値・分散は,覚えておいてもよいでしょう。
そもそも,二項分布とは何ぞやという人のために,軽く二項分布の定義を復習しておきましょう。
0<p<1 ,\,\, n は正の整数とする。 k = 0,1,2,\dots, n に対して,
\color{red} P(X=k) = {}_n \mathrm{C}_k p^{k}(1-p)^{n-k}
となるとき,確率変数 X はパラメータ (n,p) に関する二項分布 (binomial distribution) に従うといい, \color{red} X\sim B(n,p) とかく。
二項分布の詳細については,以下の記事を参照してください。
二項分布の期待値(平均)の導出
まずは期待値の導出証明を行っていきましょう。
- 定義から直接証明
- ベルヌーイ分布の和を用いた証明
- 特性関数の微分を用いた証明
の3種類を紹介します。
【期待値】定義から直接証明
直接証明するには,二項定理が必要です。
証明
二項分布の定義と,二項定理により,
\small \begin{aligned}E[X] &= \sum_{k=0}^n kP(X=k) \\ &= \sum_{k=0}^n k {}_n\mathrm{C}_k p^k (1-p)^{n-k} \\ &= \sum_{k=0}^n k \frac{n!}{k!(n-k)!}p^k (1-p)^{n-k} \\ &=np \sum_{k=1}^n \frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1} (1-p)^{n-k} \\ &= np (p+(1-p))^{n-1} = np \end{aligned}
であるから, E[X]=np が求まる。
証明終
無事,証明できましたね。
【期待値】ベルヌーイ分布の和を用いた証明
二項分布は,パラメータ p の独立なベルヌーイ分布に従う確率変数 X_1,X_2,\dots, X_n を用いて,
X \stackrel{\mathrm{d}}{=} X_1+X_2+\cdots + X_n
と書き表せるのでした(ただし,\stackrel{\mathrm{d}}{=} は分布の意味で等しいことを表す)。これを用いると,以下のような証明が可能です。
証明
X\sim B(n,p) とすると, X は,パラメータ p の独立なベルヌーイ分布に従う確率変数 X_1,X_2,\dots, X_n を用いて,
X \stackrel{\mathrm{d}}{=} X_1+X_2+\cdots + X_n
とかける。 E[X_k] = p であるから,
がわかる。
証明終
【期待値】特性関数の微分を用いた証明
期待値は,特性関数を微分する形でも証明することができます。まずは,二項分布の特性関数を確認しましょう。
X\sim B(n,p) とするとき,
\color{red} E[e^{itX}] = (1-p+pe^{it})^n.これを用いると,以下のような証明も可能です。
証明
特性関数の両辺 t で微分すると,
E[iXe^{itX}] = n (1-p+pe^{it})^{n-1} ipe^{it}
であり, t= 0 を代入すると,
よって, E[X] = np がわかる。
証明終
微分の左辺は,厳密には期待値(和)と微分の交換を行っていますが,今の場合,期待値の計算は単なる有限和であるため,交換は容易に正当化されます。
なお,今回は「特性関数」を微分しましたが,「積率母関数(モーメント母関数)」を微分しても同様に得ることができます。
二項分布の分散の導出
分散の証明も,
- 定義から直接証明
- ベルヌーイ分布の和を用いた証明
- 特性関数の微分を用いた証明
の順に述べましょう。
【分散】定義から直接証明
まず,2次モーメント E[X^2 ] を示し,公式 V(X)=E[X^2]-E[X]^2 を用いて導出しましょう。
証明
まず,2次モーメントについて,
\small \begin{aligned} &E(X^2)\\ &= \sum_{k=0}^n k^2 P(X=k) \\ &= \sum_{k=0}^n k^2 {}_n\mathrm{C}_k p^k (1-p)^{n-k} \\ &= np \sum_{k=1}^n k \frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1} (1-p)^{n-k} \\ &= np \sum_{k=1}^n \frac{\{(k-1)+1\}(n-1)!}{(k-1)!(n-k)!}p^{k-1} (1-p)^{n-k} \\ &= np \biggl\{(n-1)p\sum_{k=2}^n \frac{(n-2)!}{(k-2)!(n-k)!}p^{k-2} (1-p)^{n-k}\\ &\qquad+ \sum_{k=1}^n \frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1} (1-p)^{n-k} \biggr\}\\ &= np\bigl\{ (n-1)p (p+(1-p))^{n-2}\\ &\qquad + (p+(1-p))^{n-1}\bigr\} \\ &= np((n-1)p+1) \end{aligned}
であるから,分散については,
がわかる。
証明終
途中, n-2 乗の項が出てきていますが,前に係数 n-1 がついているので, n=1 のときは,この項は消えます。
【分散】 ベルヌーイ分布の和を用いた証明
確率変数 X,Y が独立であれば, V(X+Y) = V(X)+V(Y) が成立することを用いましょう。
証明
X\sim B(n,p) とすると, X は,パラメータ p の独立なベルヌーイ分布に従う確率変数 X_1,X_2,\dots, X_n を用いて,
X \stackrel{\mathrm{d}}{=} X_1+X_2+\cdots + X_n
とかける。 V(X_k) = p(1-p) であるから,
がわかる。
証明終
【分散】特性関数の微分を用いた証明
期待値と同様,特性関数を用いた証明も行います。
証明
特性関数 E[e^{itX}] = (1-p+pe^{it})^n の両辺 t で2回微分すると,
\begin{aligned}& E[(ix)^2e^{itX}]\\ &= -n(n-1)p^2e^{2it} (1-p+pe^{it})^{n-2} \\ &\quad - npe^{it}(1-p+pe^{it})^{n-1}. \end{aligned}
両辺 t=0 を代入すると,
より, E[X^2] = np((n-1)p+1). これより,分散について,
がわかる。
証明終
「特性関数」を微分しましたが,「積率母関数(モーメント母関数)」を微分しても同様に得ることができるのは,期待値の導出と同様ですね。
二項分布の標準偏差
標準偏差は,分散の平方根 \sqrt{V(X)} ですから,分散の結果から
\sqrt{V(X)} = \sqrt{np(1-p) }
が直ちに出ますね。