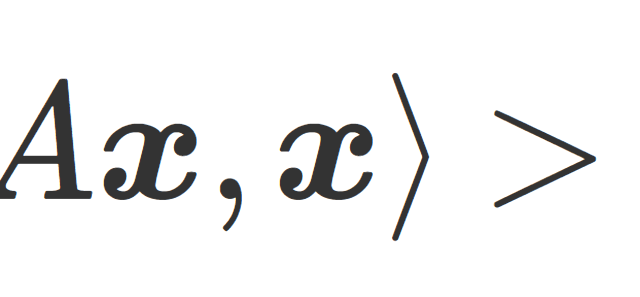 線形代数学
線形代数学 正定値行列・半正定値行列の定義・性質3つとその証明
正定値行列 (positive definite matrix) とは内積について <Ax, x>>0が成り立つ行列で,半正定値行列とは,<Ax, x>≧0 が成り立つ行列です。正定値行列・半正定値行列について,その定義と性質を紹介しましょう。
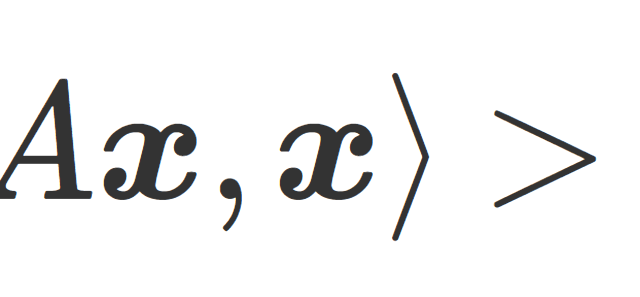 線形代数学
線形代数学  線形代数学
線形代数学  群・環・体
群・環・体 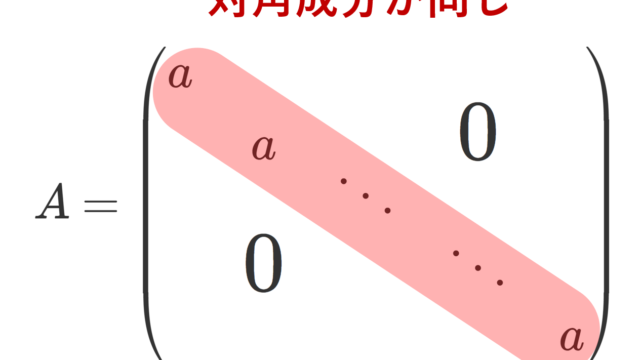 線形代数学
線形代数学 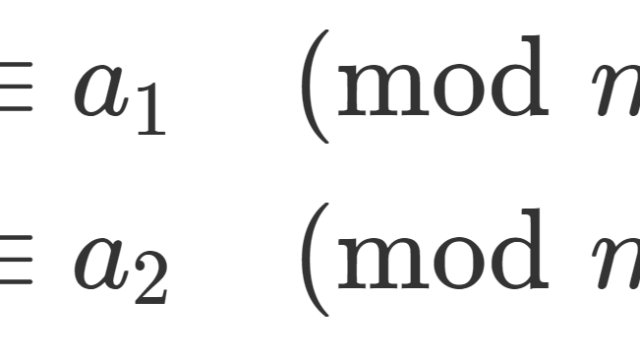 数論
数論 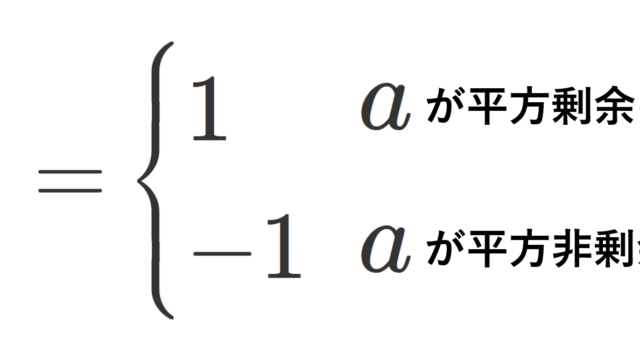 数論
数論 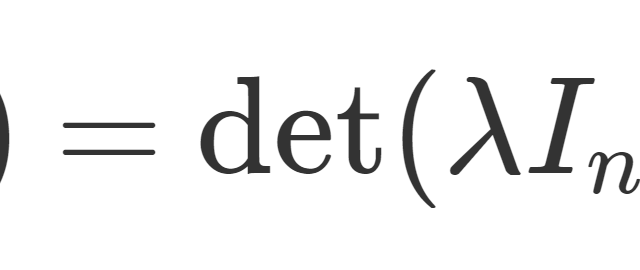 線形代数学
線形代数学 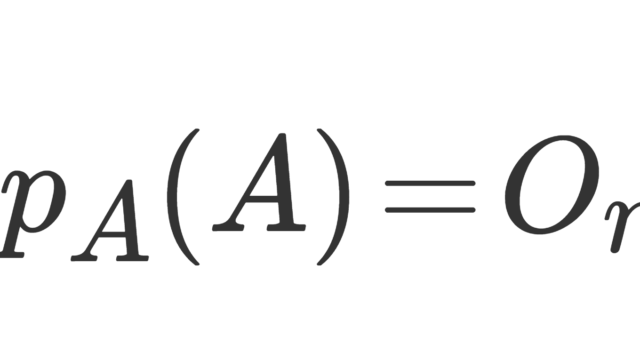 線形代数学
線形代数学 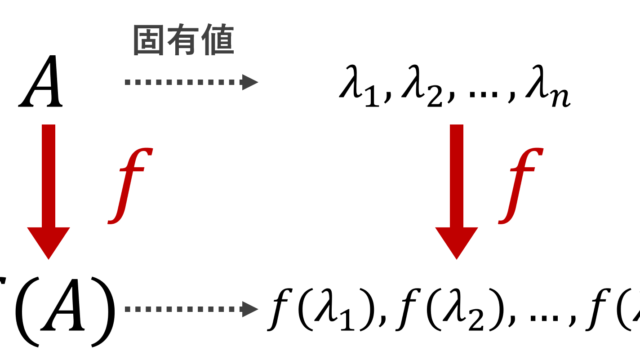 線形代数学
線形代数学 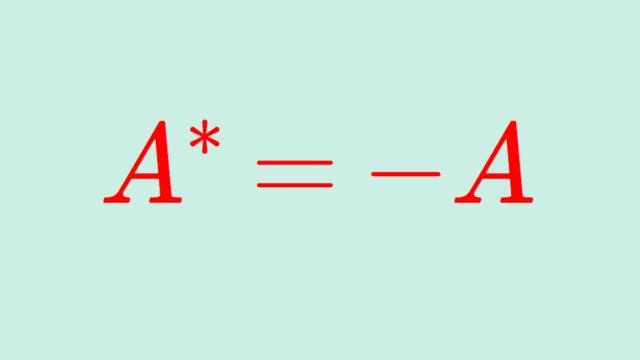 線形代数学
線形代数学