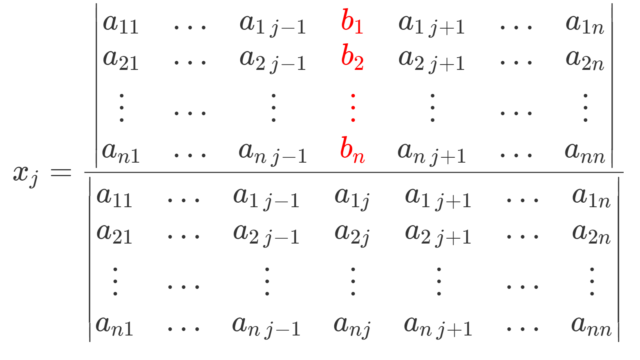 線形代数学
線形代数学 クラメルの公式とその例題・証明をていねいに
連立一次方程式の解法の1つに,「クラメルの公式 (Cramer's rule)」というものがあります。これは,連立一次方程式の解を,行列式で表そうとするものです。これについて,その内容と具体例・証明を詳しく解説しましょう。
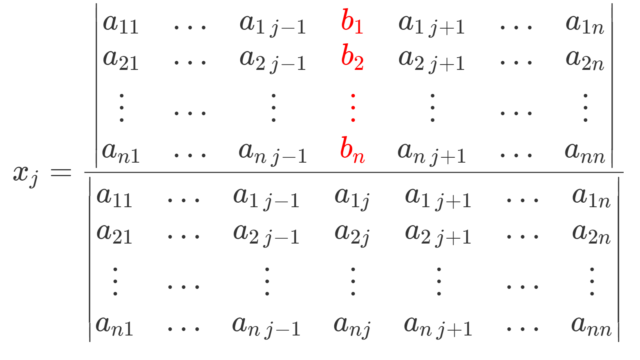 線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学  線形代数学
線形代数学 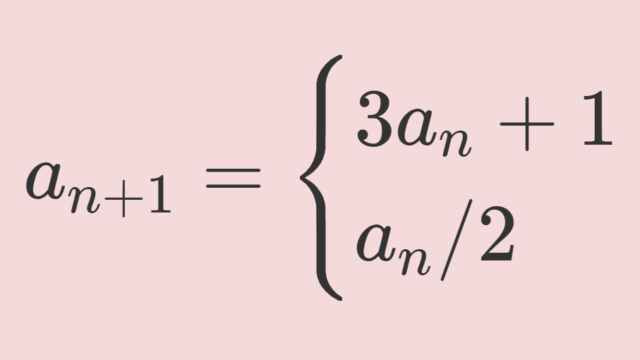 数論
数論