微分積分学(大学) 一様収束と各点収束の違いを4つの例とともに理解する
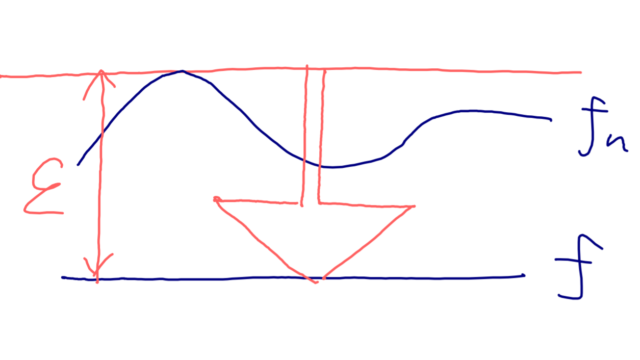
大学数学においては必須である，関数列の一様収束 (uniformly convergence) と各点収束 (pointwise convergence) の違いを定義や具体例とともに正しく理解し，イメージを膨らませられるようにしていきましょう。
微分積分学(大学)
微分積分学(大学) 
微分積分学(大学) 【ディニの定理】各点収束から一様収束が従う定理とその証明
連続関数の列が単調増加に連続関数へ各点収束するとき，一様収束が言える「ディニの定理 (Dini's theorem) 」と呼ばれる定理があります。本記事ではこの定理の紹介とポイント解説，最後に証明を行います。証明のみ位相空間論の知識が必要です。
微分積分学(大学) アスコリ–アルツェラの定理とその証明～注意点を添えて～
アスコリ–アルツェラの定理（Ascoli–Arzelà theorem）は，解析学でよく使われる定理の一つですが，用語が難しく，適用条件にも注意が必要です。まず必要な用語として，「一様有界性」と「同程度連続性」の定義をし，定理を紹介します。
微分積分学(大学) 【Frodaの定理】単調関数の不連続点は高々可算個であることの証明
広義単調増加，または広義単調減少な関数は，不連続点があってもそれは高々可算個しかないことを証明します。証明は比較的シンプルだと思います。私も，最初にこの定理の証明を見たときはあまりにシンプルで感動しました。皆さんともこの感動を共有できると幸いです！
微分積分学(大学) 級数が絶対収束すれば収束することの2通りの証明
ある数列に対し，その絶対値の和が収束することを絶対収束といいます。級数が絶対収束すれば元の数列が収束することを，一つはコーシー列を使った一般的な方法で，もう一つは高校生にも理解できる方法で証明してみたいと思います。
微分積分学(大学) 交代級数の収束性の証明とその具体例
正の項と負の項が交互に現れる級数を交代級数 (alternating series) といいます。今回は，ライプニッツの定理ともいわれる，単調減少かつ０に収束する非負な数列の交代級数の和が収束することを証明します。最後には，その一般化も述べます。