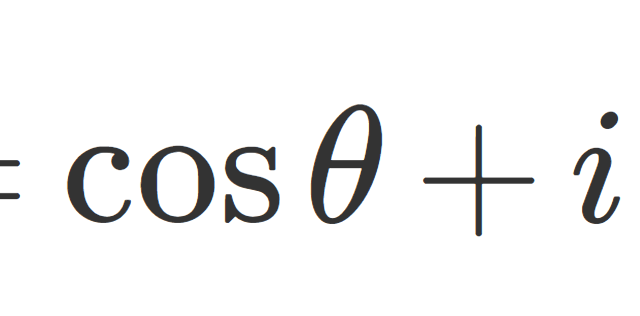複素関数論 オイラーの公式・オイラーの等式とは～美しい等式の紹介～
オイラーの公式 (Euler's formula) とは，e^{iΘ} = cos Θ+i sin Θ で，オイラーの等式 (Euler's identity) とは，それに Θ = π を代入した等式 e^{iπ} =-1 を指します。これらの公式・等式がどういった意味で成立するのか，その証明と関連公式の解説を行いましょう。
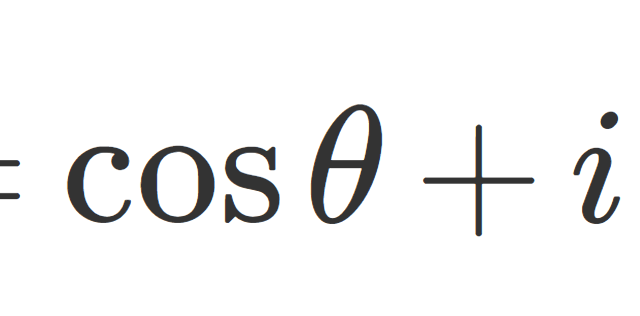複素関数論
複素関数論 
複素関数論 複素関数の微分～定義と例～
複素数の関数における微分は，実数のときと同じく，lim_{h→0} (f(z+h)-f(z))/h の形で定義されます。これについて，具体例を交えて詳しく解説します。
複素関数論 フレネル積分(sin(x^2)の積分)とその導出証明
フレネル積分 (Fresnel integral) は，sin(x^2), cos(x^2) の積分を指します。これについて，その公式と，複素関数論でよく用いられる経路積分を用いた詳しい証明を紹介しましょう。
複素関数論 複素数版のガウス積分とその導出証明
ガウス積分 (Gaussian integral) の指数部分を複素数に拡張したものについて，その形の紹介と，導出の証明を行いましょう。
複素関数論 コーシーリーマンの関係式とそのわかりやすい証明
複素関数論におけるコーシーリーマンの関係式 (Cauchy-Riemann equation)について，その定理の主張と証明を紹介しましょう。
微分積分学(大学) ガンマ関数とは～定義と性質をわかりやすく～
階乗の一般化であり，解析学でよく使われる関数であるガンマ関数 (Gamma function) について，その定義と性質を詳しく述べましょう。
微分積分学(大学) べき級数におけるアーベルの定理とその応用例・証明
べき級数におけるアーベルの定理（アーベルの連続性定理; Abel's theorem）について，その定理の主張と応用例，そして証明を述べましょう。実数の場合と複素数の場合の両方を別々に扱います。