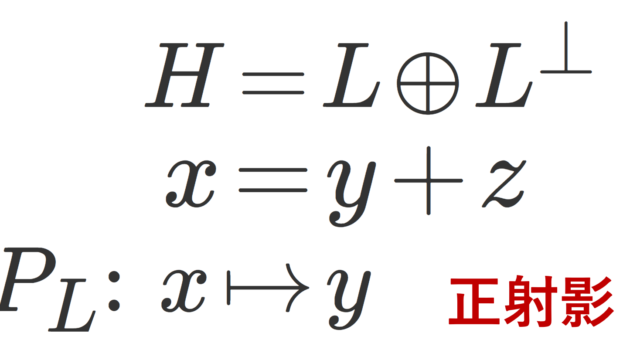 関数解析学
関数解析学 ヒルベルト空間における正射影・正射影作用素
ヒルベルト空間における正射影(projection)あるいは直交射影について,その定義を紹介し,関連して正規直交系が与えられた部分空間上への射影について考えましょう。
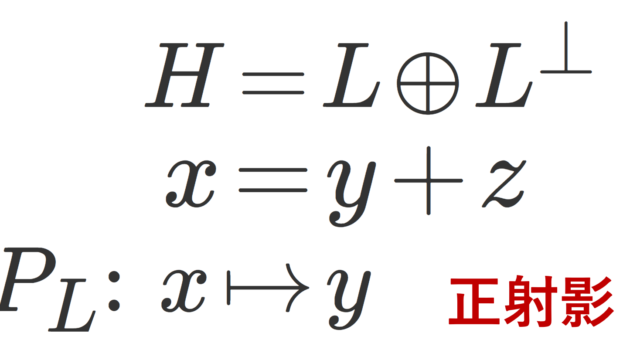 関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学 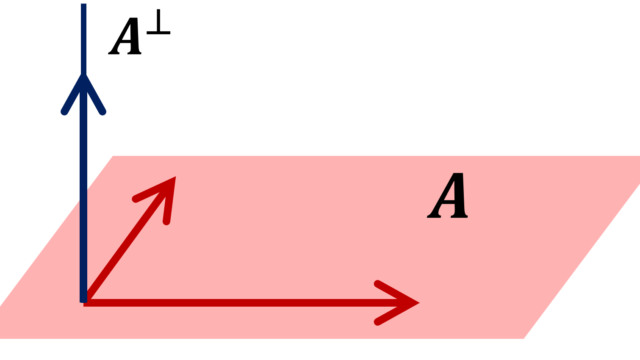 関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学  関数解析学
関数解析学