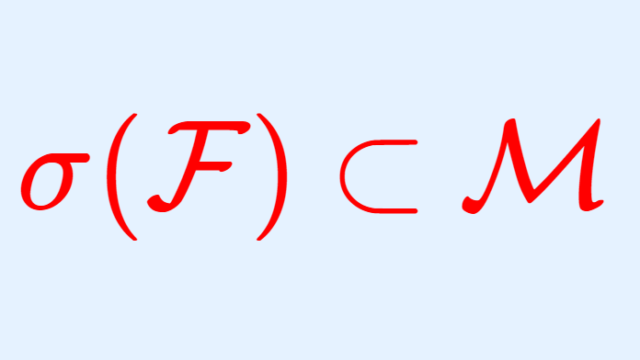 測度論
測度論 単調族の定義と単調族定理の証明
集合の部分集合族が「単調族 (monotone class) 」であるとは,無限個の集合の上昇列や下降列に関して閉じていることを言います。単調族について,その詳しい定義と,有名で大切な単調族定理の証明を行いましょう。
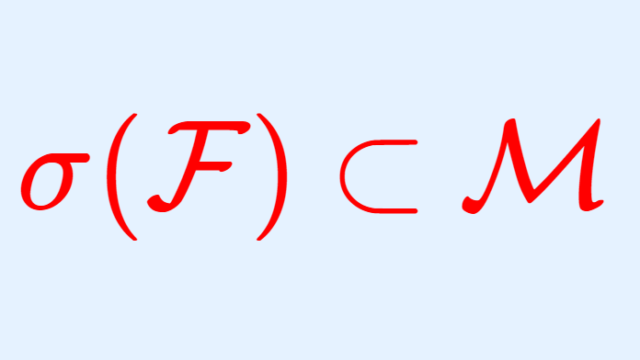 測度論
測度論 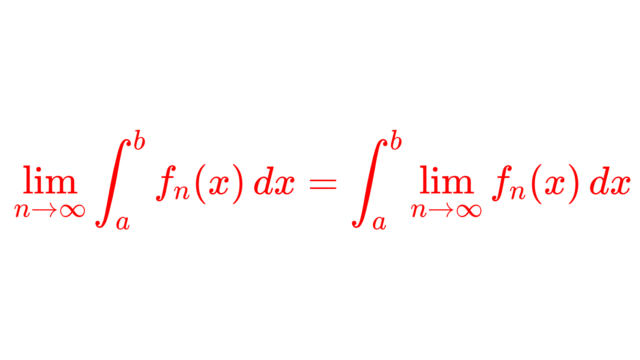 測度論
測度論 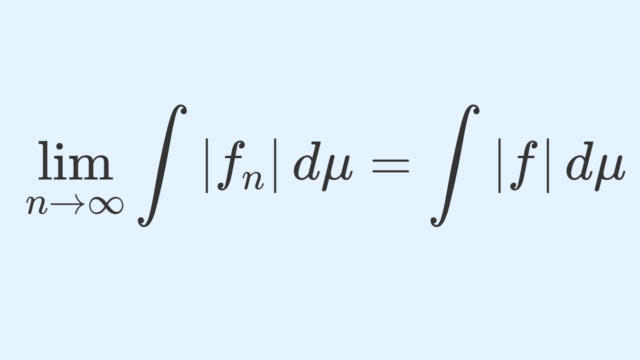 測度論
測度論  測度論
測度論  測度論
測度論  測度論
測度論  測度論
測度論 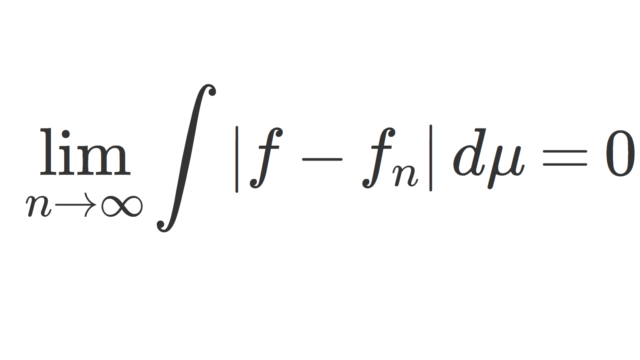 測度論
測度論 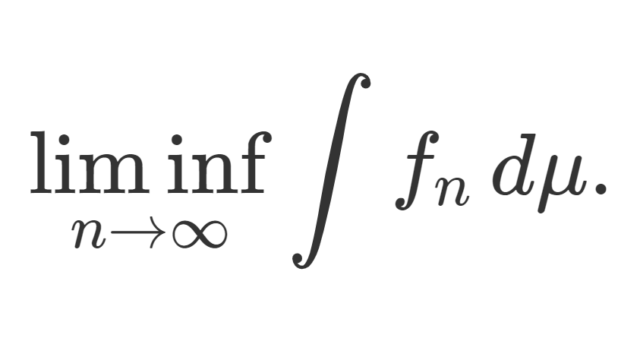 測度論
測度論 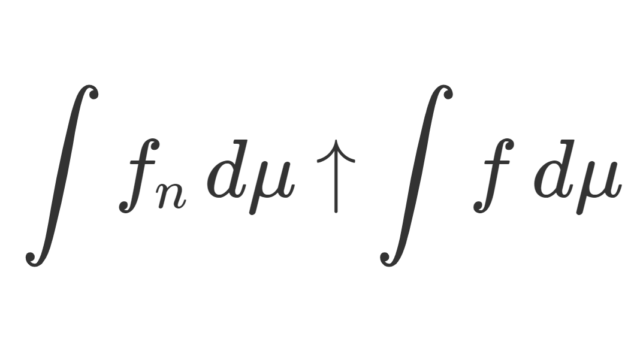 測度論
測度論