 解析学(大学)その他
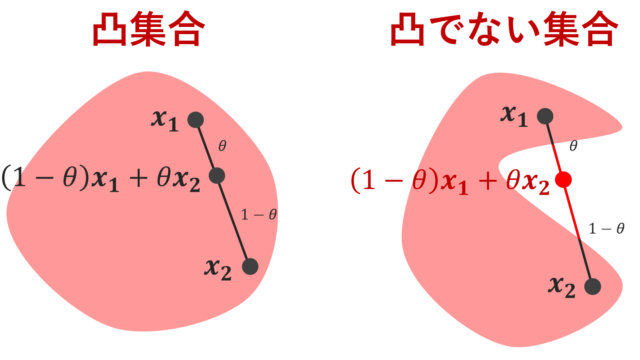
解析学(大学)その他 凸集合とは何かをわかりやすく~定義と性質~
凸集合 (convex set) とは簡単に言うと「へっこんでいない集合」のことをいいます。これについて,ちゃんとした定義と,性質を解説します。
 解析学(大学)その他
解析学(大学)その他  統計学
統計学 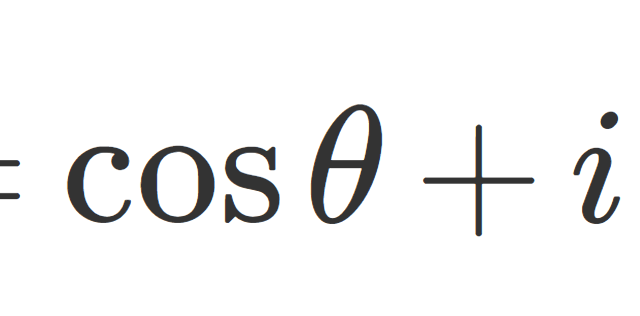 複素関数論
複素関数論  複素関数論
複素関数論  統計学
統計学 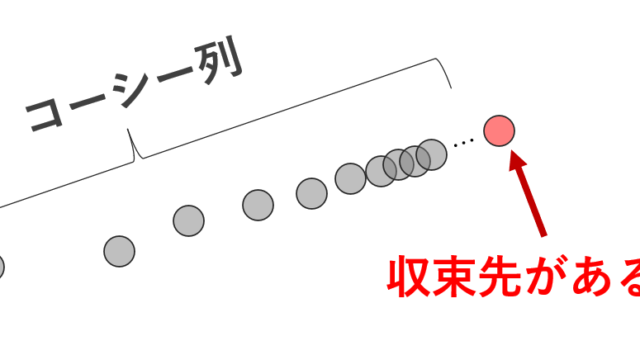 集合と位相
集合と位相 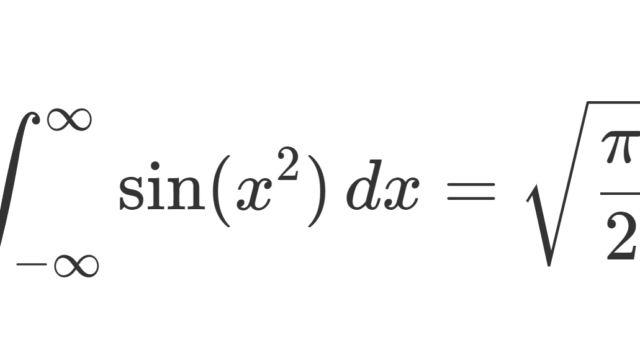 複素関数論
複素関数論 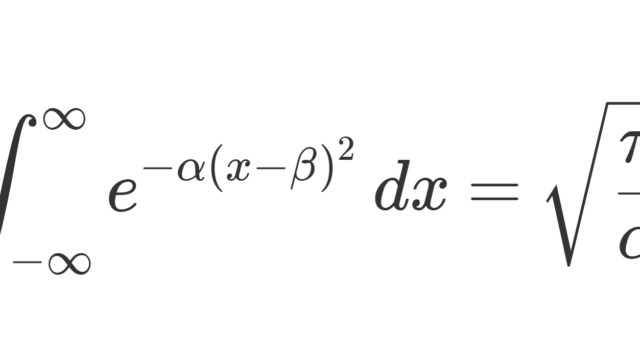 複素関数論
複素関数論 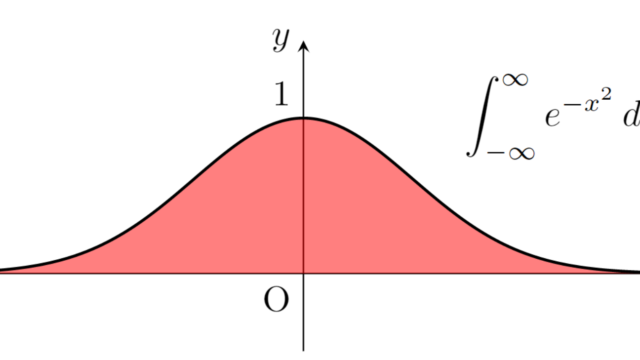 微分積分学(大学)
微分積分学(大学) 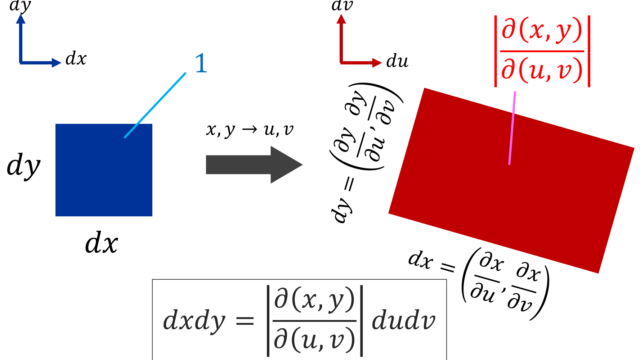 微分積分学(大学)
微分積分学(大学)