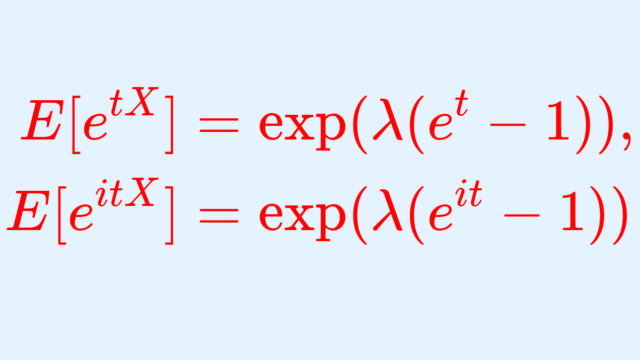 確率論
確率論 ポアソン分布の積率母関数(モーメント母関数)・特性関数の導出証明
ポアソン分布の積率母関数(モーメント母関数)と特性関数について,その導出の証明を行いましょう。
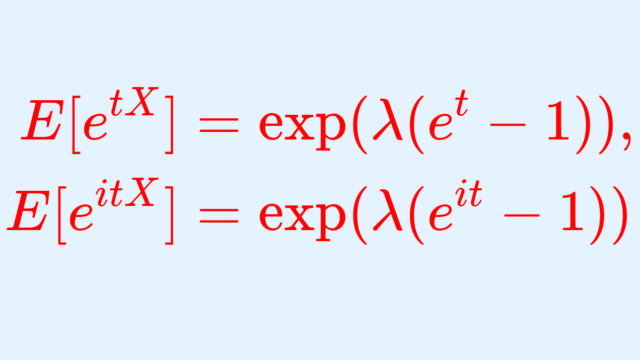 確率論
確率論  確率論
確率論  確率論
確率論 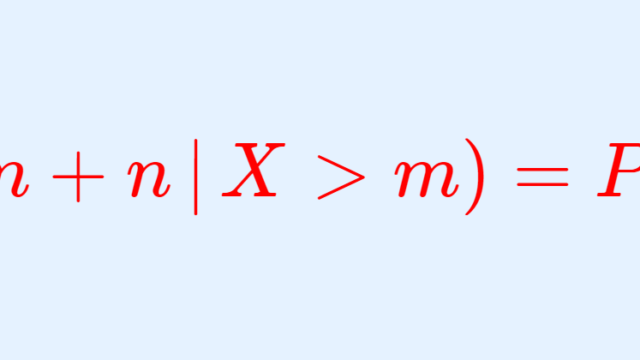 確率論
確率論 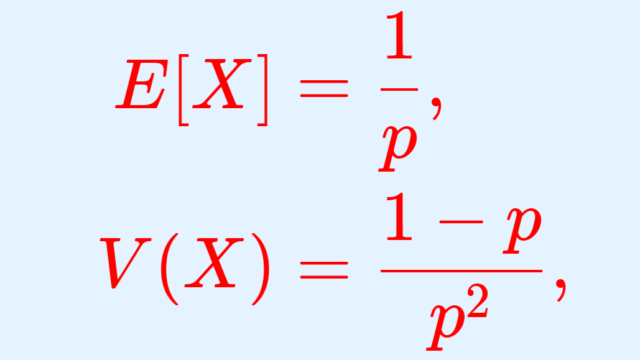 確率論
確率論 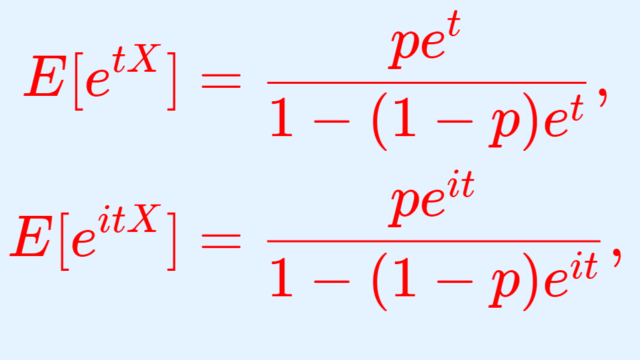 確率論
確率論 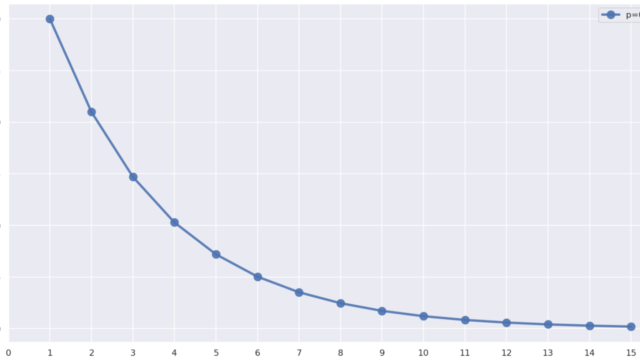 確率論
確率論  確率論
確率論  確率論
確率論 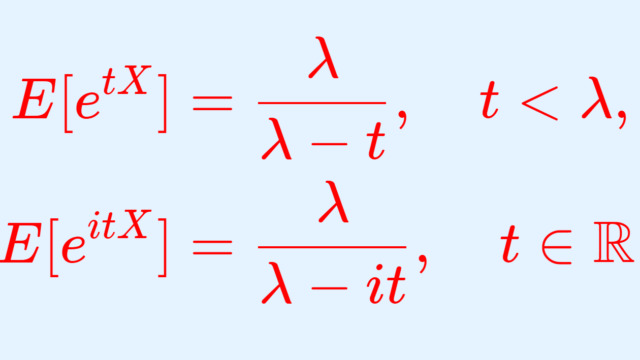 確率論
確率論