 集合と位相
集合と位相 ベルンシュタインの定理とその証明【双方単射があれば全単射がある】
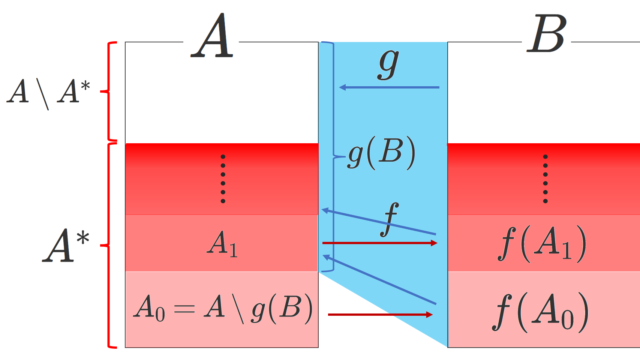
ベルンシュタインの定理(Schröder–Bernstein theorem)とは,2つの集合それぞれを定義域・終域とする双方向の単射があれば,全単射があるという定理です。ベルンシュタインの定理について,イメージ図を交えて証明していきましょう。
 集合と位相
集合と位相  解析学(大学)その他
解析学(大学)その他  測度論
測度論  解析学(大学)その他
解析学(大学)その他 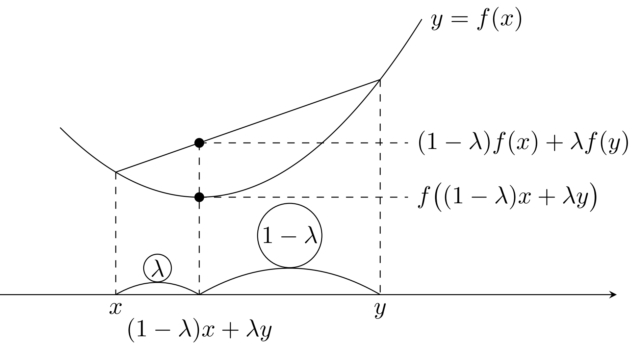 解析学(大学)その他
解析学(大学)その他 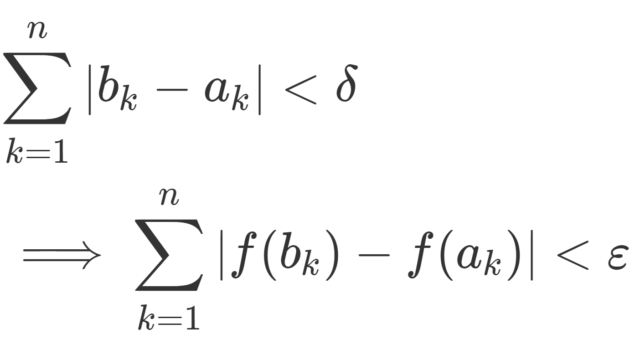 解析学(大学)その他
解析学(大学)その他 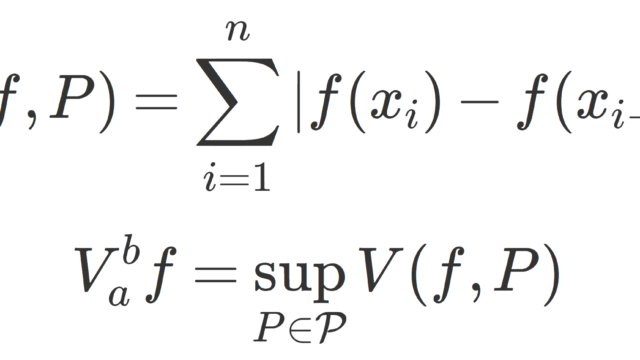 解析学(大学)その他
解析学(大学)その他 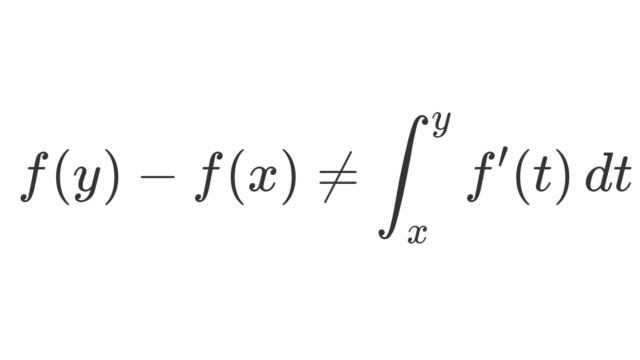 測度論
測度論 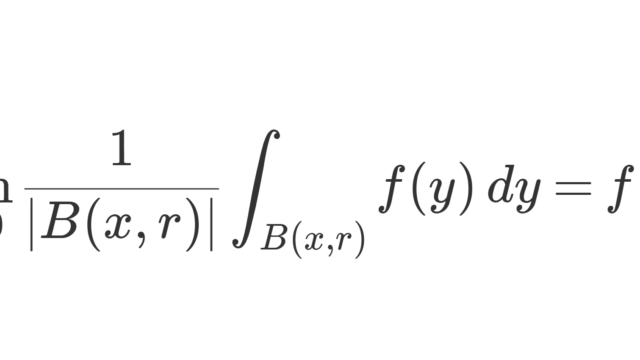 測度論
測度論 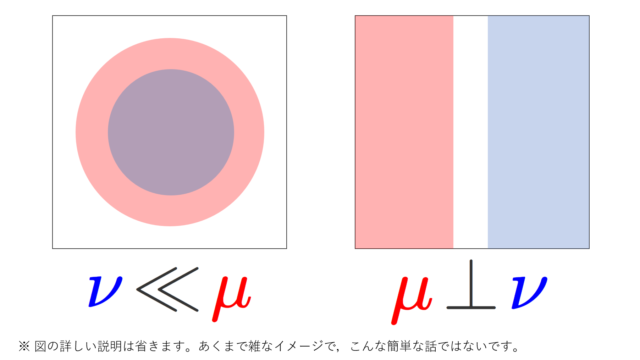 測度論
測度論