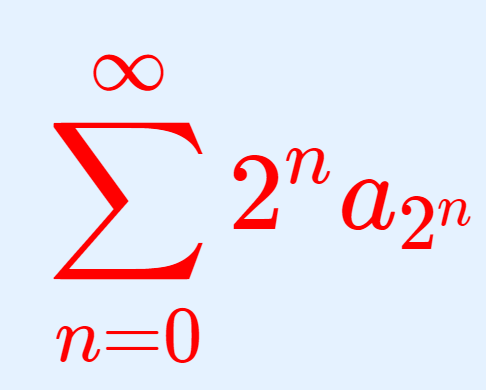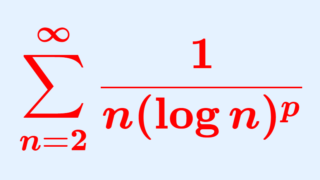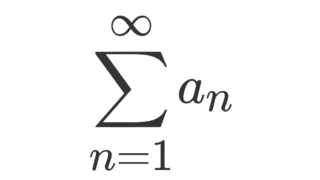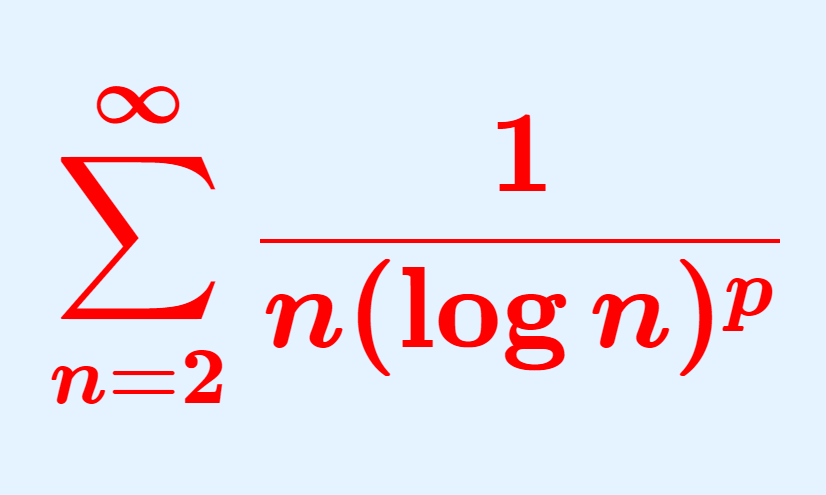【級数の収束判定法】Cauchy Condensation Test

級数の収束判定法の1つである，Cauchy condensation test（あるいは日本語で「コーシーの凝集判定法」）について，その主張と証明を追いましょう。

定理 (Cauchy Condensation Test)

$\{a_n\}$ は非負かつ広義単調減少（すなわち $a_1\ge a_2 \ge a_3 \ge \dots \ge 0$ ）となる数列と仮定する。
このとき，級数 $\displaystyle \sum_{n=1}^\infty a_n$ が収束する必要十分条件は

\color{red} \sum_{n=0}^\infty 2^n a_{2^n}

が収束することである。

各項を見るのではなく，第 $2^n$ 項のみを condensation (凝集) して，収束を判定するということで，Condensation test といわれるんですね。

Cauchy Condensation Test の証明

早速証明を行いましょう。

証明

$\{a_n\}$ は非負かつ広義単調減少であるから，

\sum_{k=2^n+1}^{2^{n+1}} a_k\le 2^n a_{2^n} \le 2\sum_{k=2^{n-1}+1}^{2^n} a_k

である。（ $n=0$ のときは $a_2 \le a_1 \le 2a_1$ と解釈する。）各辺 $\sum_{n=0}^\infty$ を計算することで，

\sum_{n=2}^\infty a_n \le \sum_{n=0}^\infty 2^n a_{2^n} \le 2\sum_{n=1}^\infty a_n

を得る。よって題意は示された。

証明終

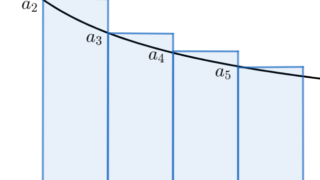
証明自体は，非常に簡単なものでしたね。証明の方針は，「単調性を活かして，上下から抑える」ですが，この方針自体は，広義積分による収束判定法（→ 【級数】広義積分による収束判定法と1/n^pの和の収束・発散）と非常に似ています。

具体例を2つ挙げましょう。

例1 ( $1/n^p$ の和の収束・発散).

$\color{red} a_n = 1/n^p$ とすると，

\sum_{n=0}^\infty 2^n a_{2^n} = \sum_{n=0}^\infty 2^{n(1-p)}

であるから， $\sum_{n=1}^\infty 1/n^p$ は

$\sum_{n=1}^\infty 1/n^p$ の収束・発散の事実は，広義積分を用いた収束判定の方が有名でしょう。これについては，以下の記事も参照してください。

例2 ( $1/n(\log n)^p$ の和の収束・発散).

$\color{red} a_n = 1/n(\log n)^p$ とすると，

\sum_{n=1}^\infty 2^n a_{2^n} = \sum_{n=1}^\infty\frac{1}{(n\log 2)^p}

であるから，例1.により， $\sum_{n=2}^\infty 1/n(\log n)^p$ は

これも，広義積分による収束判定法の方が有名でしょう。その方法については，以下の記事で解説しています。