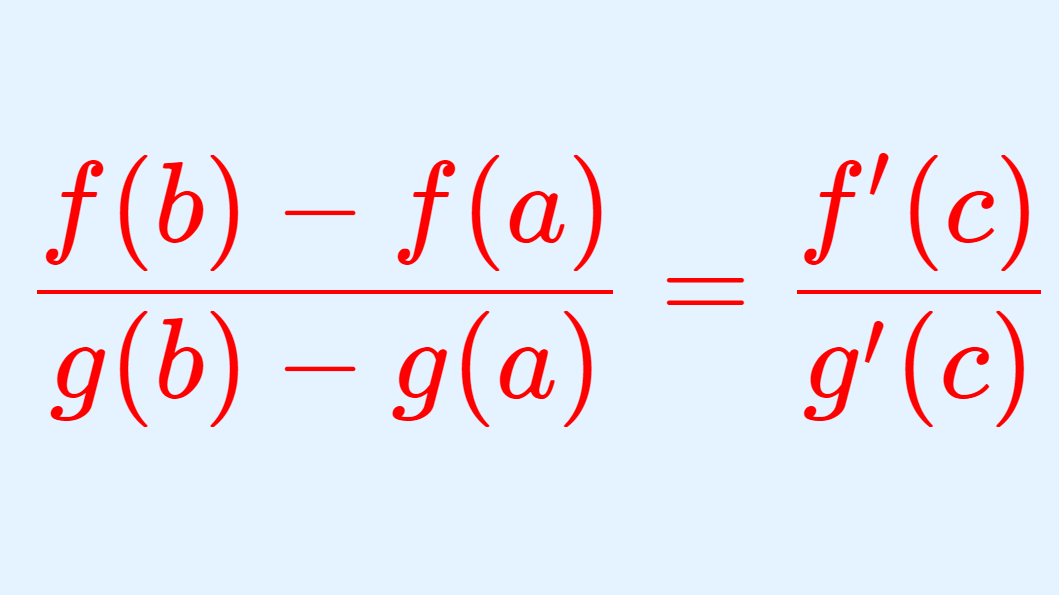普通の平均値の定理(ラグランジュの平均値の定理)を拡張した「コーシーの平均値の定理」について,その主張と証明を述べます。
コーシーの平均値の定理
コーシーの平均値の定理 (Cauchy’s mean value theorem)
関数 f,g は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき, g'(x) \ne 0 \,\,(a < x < b) ならば,
\color{red} \frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f'(c)}{g'(c)} , \quad a < c< b
となる c が存在する。
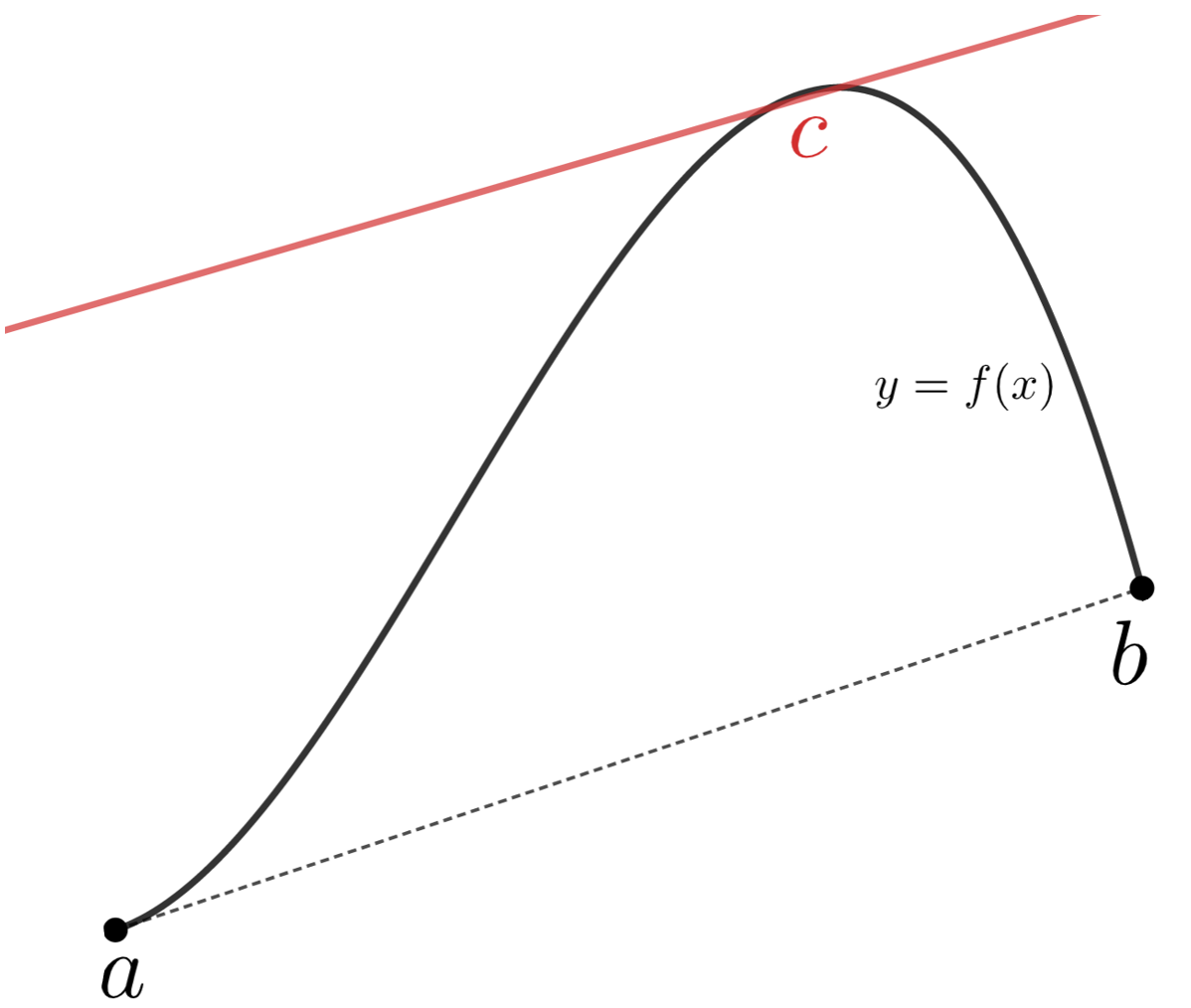
これは,高校で習う(ラグランジュの)平均値の定理の一般化になっています。平均値の定理の主張を確認しておきましょう。
関数 f は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき,
\color{red} \frac{f(b)-f(a)}{b-a} = f'(c) , \quad a < c< b
となる c が存在する。
実際,コーシーの平均値の定理において g(x) = x とおくと,これが得られますね。(ラグランジュの)平均値の定理とその証明については以下で解説しています。
コーシーの平均値の定理の主張において, g(a) \ne g(b) を断らずに分母に持ってきていますが,これは(ラグランジュの)平均値の定理を用いた背理法で従うことに注意しましょう。
実際,もし g(a) = g(b) とすると,(ラグランジュの)平均値の定理により, g'(c) = 0 となる c が存在せねばなりません。これは仮定に矛盾しています。
なお,割り算しない \color{red} f'(c)(g(b)-g(a)) = g'(c)(f(b)-f(a)) の形をコーシーの平均値の定理ということもあります。このとき, g'(x) \ne 0 \,\,(a < x < b) の条件は不要になります。
コーシーの平均値の定理の証明
早速証明していきましょう。証明はラグランジュの平均値の定理のときと同様に,以下のロルの定理に帰着させます。
関数 f は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能であるとする。このとき, f(a) = f(b) ならば,
\color{red} f'(c) = 0 , \quad a < c< b
となる c が存在する。
これの証明は,平均値の定理・ロルの定理とその証明を参照してください。
さて,コーシーの平均値の定理を証明しましょう。
証明
\varphi(x) = \{g(b)-g(a)\} \{ f(x) - f(a)\} - \{ f(b)-f(a)\} \{g(x)-g(a)\}
とおくと, \varphi は閉区間 [a,b] で連続かつ開区間 (a, b) で微分可能である。また, \varphi(a) = \varphi(b) = 0 であるから,ロルの定理により, \varphi'(c) = 0 となる a<c<b が存在する。ここで,
であるから,特に
を得る。
証明終
見事に証明できましたね。
その他の平均値の定理
平均値の定理のその他のバージョンについて,その主張を紹介しておきましょう。
積分の平均値の定理
積分の平均値の定理
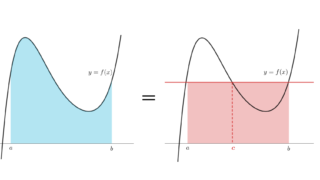
f は [a,b] 上連続かつ積分可能とする。このとき,
\color{red} f(c) = \frac{1}{b-a} \int_a^b f(x)\, dx
となる a<c<b が存在する。
積分バージョンの平均値の定理です。右辺が「積分の平均」になっていますね。これについては,以下の記事で解説しています。