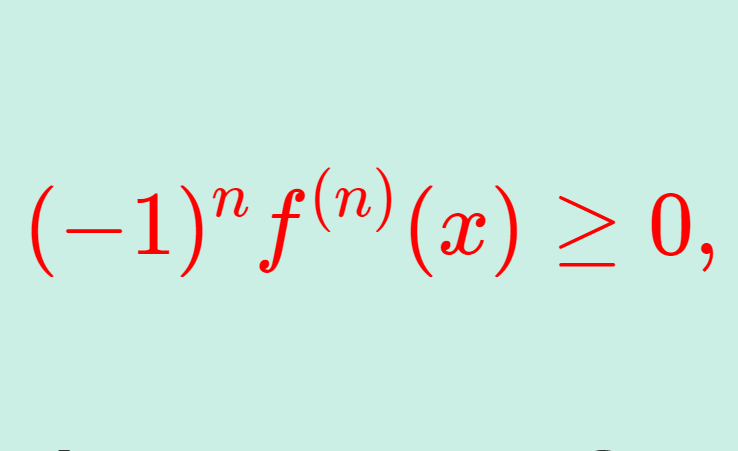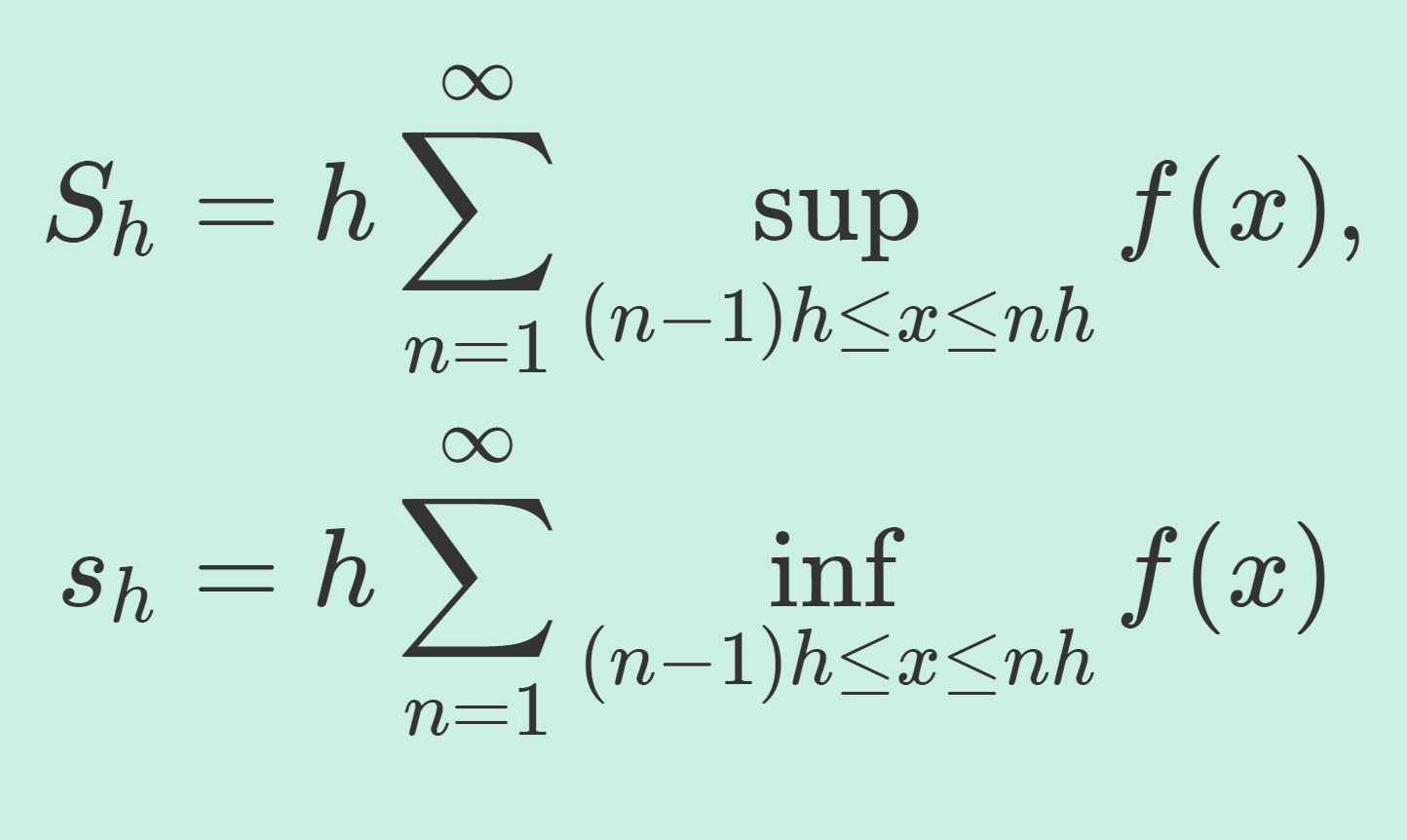Completely monotone function という,通常の monotone function (単調な関数) よりも性質の良い関数について紹介します。
Completely monotone functionの定義
定義 (completely monotone function)
関数 f\colon (0,\infty)\to [0,\infty) が C^\infty 級(無限回微分可能)であり,
\color{red}(-1)^n f^{(n)} (x) \ge 0,\quad x\in (0,\infty), \; n\ge 1
をみたすとき, f を completely monotone function (cmf) という。
不等式について, n=1 とすると,f'(x)\le 0 ですから,completely monotone function は単調減少になっていますね。
たとえば, Ce^{-ax}\; (C, a>0), \;\; x^{-\alpha} \; ( \alpha >0) は cmf です。
Completely monotone functionの性質
Completely monotone function の重要な性質を述べておきましょう。以下は基本的な性質です。
定理1 (see, e.g., [1, Corollary 1.6])
f,g \colon (0,\infty)\to [0,\infty) は cmf であり,s,t>0 とする。このとき, \color{red} sf +tg も cmf である。
これは,定義から容易に確認できますね。さらに,関数列の極限に対しても閉じています。
定理2 (see, e.g., [1, Corollary 1.7])
\{f_n\} を cmf の列とし, f に各点収束しているとする。このとき,この収束は広義一様収束であり, f も cmf である。さらに各微分の列 \{f^{(k)}_n\} も f^{(k)} に広義一様収束する。
さらに,cmf はかなり明示的な形でかけることが知られています。それが以下の Bernstein の定理です。
定理3 (Bernstein; see, e.g., [1, Theorem 1.4]).
f\colon (0,\infty)\to [0,\infty) が cmf ならば,ある [0,\infty) 上の測度 \mu が存在して,
\color{red} f(x)=\int_{[0,\infty)} e^{-xt}\,\mu(dt),\quad x>0
とかける。逆に,上の式の右辺が任意の x>0 で有限であれば,これは cmf である。
cmf ならば,ある測度のラプラス変換の形でかける,と言っているんですね。これの証明は,長くなりますから,省略します。
たとえば, Ce^{-ax}\; (C, a>0), \;\; x^{-\alpha} \; ( \alpha >0) はそれぞれ
\begin{aligned}Ce^{-ax} &= C\int_{[0,\infty)} e^{-xt}\, \delta_a(dt),\\ x^{-\alpha} &= \frac{1}{\Gamma(\alpha)}\int_0^\infty e^{-xt}t^{\alpha -1}\, dt \end{aligned}
とかけますね。ただし, \delta_a は a に 1 の重みがあるデルタ測度で, \Gamma はガンマ関数です。
以上の他にも,completely monotone function には,さまざまな良い性質が備わっています。詳しくは,以下の参考文献などを見てみてください。
参考
- R. Schilling. et. el. Bernstein Functions Theory and Applications. 2nd Edition, De Gruyter, 2012.