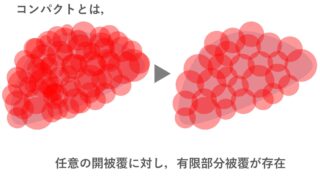
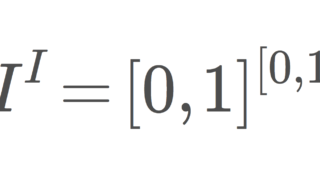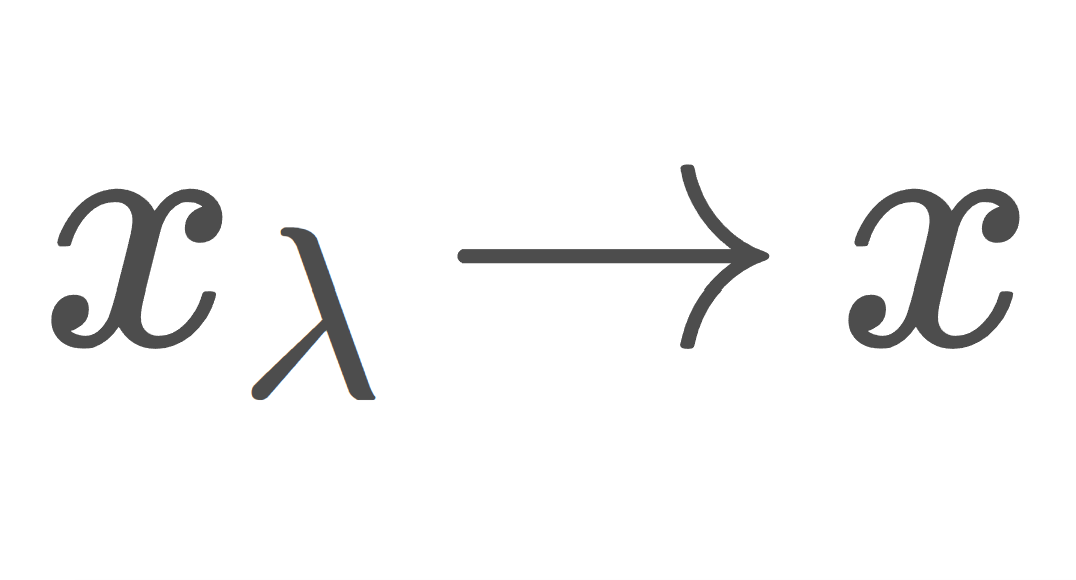可算コンパクトとは，任意の可算開被覆が，有限部分被覆をもつ空間のことを言います。「可算」ではなく任意の濃度を許すと，コンパクトの定義になります。
可算コンパクトについて，その定義と性質の証明・具体例を紹介しましょう。
可算コンパクトの定義
定義（可算コンパクト）
(X,\mathcal{O}) を位相空間とし， A\subset X とする。
A の任意の可算個の開被覆 \mathcal{C} に対し，有限部分被覆 \mathcal{C}_0\subset \mathcal{C} が存在するとき， A を可算コンパクト集合 (countably compact set) であるという。
さらに， X 自体が可算コンパクト集合であるとき， (X,\mathcal{O}) は可算コンパクト空間 (countably compact space) であるという。
すなわち，集合 A\subset X が可算個の開集合族 \{O_n\} に対し， A\subset \bigcup_{n=1}^\infty O_n となるならば，ここから有限個 O_{n_1}, \ldots, O_{n_k} を選んできて， A\subset \bigcup_{i=1}^k O_{n_i} とできることを可算コンパクトといいます。
上の赤字「可算個」の条件を外したものが普通のコンパクトの定義です。任意の開被覆に対し，有限部分被覆が存在するのがコンパクトの定義なのに対し，可算コンパクトは開被覆が可算個である場合に限って，有限部分被覆が存在するものをいいます。よって，明らかにコンパクトならば可算コンパクトです。
可算コンパクトの性質
具体例の前に，性質を一通り紹介しましょう。
1. 可算コンパクトと同値な性質
定理1（可算コンパクトと同値な性質）
(X, \mathcal{O}) を位相空間とし，\mathcal{F} を閉集合族とする。このとき，以下は同値である。
- X は可算コンパクト
- 任意の点列 (x_n)\subset X が集積点をもつ
- 任意の無限集合 A\subset X が \omega-集積点をもつ。すなわち，ある点 a\in X が存在して， a の任意の開近傍 U_a に対し，U_a\cap A が無限集合となる
- 可算個の閉集合族 \mathcal{D}\subset \mathcal{F} が有限交叉性をもつならば， \bigcap_{D\in \mathcal{D}}D\ne \emptyset である
集合族 \mathcal{D} が有限交叉性をもつとは， \mathcal{D} に属する任意の有限個の部分集合の共通部分が空でないことを言います。
1. \iff4.について
通常のコンパクトと有限交叉性の証明とほぼ同じである。コンパクト空間とコンパクト集合について詳しくを参照せよ。
4.\implies 2.について
(x_n)\subset X を点列とする。 F_n = \overline{\{ x_n\mid n\ge 1\}} とすると，可算個の閉集合族 \{F_n\} は有限交叉性をもつので，x\in \bigcap_{n=1}^\infty F_n が存在する。この x が集積点である。
2.\implies 4.について
可算個の閉集合族 \{F_n\} は有限交叉性をもつとする。このとき，各 n\ge 1 について，
x_n\in F_1\cap F_2\cap \cdots \cap F_n
とすると，2.の仮定より，点列 (x_n) には集積点 x\in X が存在する。 x_n の定義から，
であることと，右辺は閉集合より， x\in F_1\cap F_2\cap \cdots \cap F_n であり，これが任意の n\ge 1 で成立するので， x\in \bigcap_{n=1}^\infty F_n である。
2. \iff3.について
ある点が可算集合 A の \omega-集積点であることと， A を点列と見たときの集積点であることは同値なのでいえる。
2. 可算コンパクトの基本性質
上の定理は，全ての「可算」を外しても成立します。すなわち，通常のコンパクト空間の性質と類似のものです。証明もほぼ同じなので，コンパクト空間とコンパクト集合について詳しくを見てください。
なお，ハウスドルフ空間( T_2 空間)におけるコンパクト集合は常に閉集合ですが，可算コンパクト集合はそうとは限りません。たとえば，後の例3.を確認してください。
3. コンパクトならば可算コンパクト
可算コンパクトの定義の直後に述べた通りです。
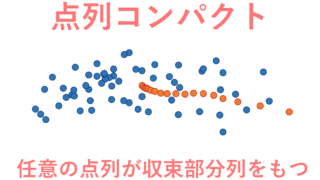
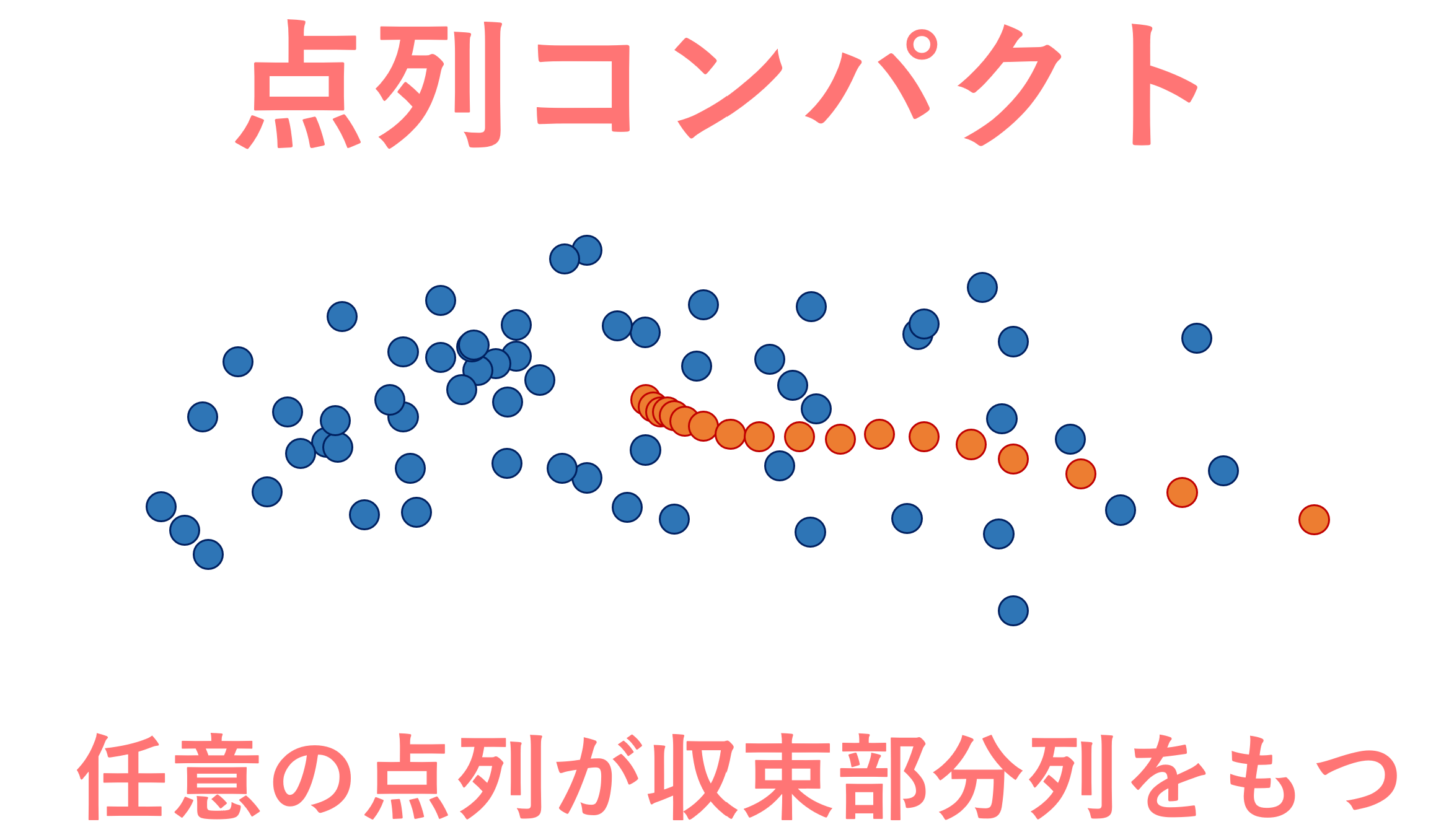
4. 点列コンパクトならば可算コンパクト
定理4（点列コンパクトなら可算コンパクト）
(X,\mathcal{O}) を位相空間とする。このとき，
X が点列コンパクトならば，可算コンパクトである。
逆に， X が第一可算のときは，可算コンパクトならば点列コンパクトも成り立つ。
点列コンパクト (sequentially compact) とは，任意の点列が収束部分列をもつことをいいます。定理1の2.で出てきた「任意の点列 (x_n)\subset X が集積点をもつ」とは，「任意の点列が収束部分ネットをもつ」ことと同値であり，点列はネット(有向点族)の一種です。よって，点列コンパクトならば可算コンパクトであることが分かります。
また，後半については，定理1の1. \implies 2.と，第一可算のときは，点列 (x_n) が集積点をもてば収束部分列が存在するので，点列コンパクトであるといえます。
注意ですが，コンパクトと点列コンパクトは一般に関連性はなく，コンパクトだが点列コンパクトでないもの，点列コンパクトだがコンパクトでないものがあります。後の例を見てください。
5. リンデレーフかつ可算コンパクトならコンパクト
これは各概念の定義より明らかです。開被覆 \mathcal{C} に対し，リンデレーフ性より，可算部分被覆 \mathcal{C}_0\subset \mathcal{C} が取れて，可算コンパクト性より，有限部分被覆 \mathcal{C}_f\subset \mathcal{C}_0 が取れますね。
本定理と，第二可算ならばリンデレーフであることから，第二可算かつ可算コンパクトならコンパクトもいえます。定理4で「第一可算のときは，可算コンパクトならば点列コンパクト」とも述べたため，第二可算のときは，コンパクト性と可算コンパクト性と点列コンパクト性は同値になります。
6. 可算コンパクトなら極限点コンパクト
定理6（可算コンパクトなら極限点コンパクト）
(X,\mathcal{O}) を位相空間とする。このとき，
- X が可算コンパクトなら極限点コンパクト(弱可算コンパクト)である
- X が極限点コンパクト(弱可算コンパクト)かつ T_1 なら可算コンパクトである
極限点コンパクト (limit point compact) あるいは弱可算コンパクト (weakly countable compact) とは，任意の無限部分集合が集積点をもつことを言います。すなわち，任意の無限集合 A\subset X に対し，ある a\in X が存在して， a の任意の開近傍 U_a に対し，U_a\cap (A\setminus \{a\})\ne\emptyset となることをいいます。
証明
1.について
定理1の3.と， \omega-集積点 \implies 集積点であることから明らか。
2.について
X を T_1 とし，無限集合 A\subset X に対し， a\in A は集積点だが \omega-集積点でないとする。このとき， a の開近傍 U で， U\cap (A\setminus\{a\}) が有限集合になるものが存在する。この有限集合を \{a_1, \ldots, a_n\} とする。 X は T_1 より， a の開近傍 U_1, \ldots, U_n で， a_1\notin U_1,\, \ldots, a_n\notin U_nとなるものが取れる。ここで，
U\cap U_1\cap \ldots \cap U_n
は，a の開近傍かつ A と共通部分をもたないので，矛盾している。よって， T_1 ならば集積点 \implies \omega-集積点なので，定理1の3.より，結論を得る。
証明終
7. 距離空間におけるコンパクトとの同値性
定理7（距離空間におけるコンパクトとの同値性）
(X, d) を距離空間とする。このとき，以下は同値である。
また，上のいずれか(したがって全て)が成立するとき，次の3つが成立する。
上の3つは一般の距離空間において同値である。
距離空間は T_1 であることと，定理6より，3.と4.は同値です。
また第二可算なら，定理5の直後に記載した内容により，1.と2.と3.の同値性が分かります。
8. 可算コンパクトと直積
定理8（可算コンパクトと直積）
(X, \mathcal{O}_X), (Y, \mathcal{O}_Y) を位相空間とする。
注意ですが， X, Y がともに可算コンパクトでも， X\times Y は可算コンパクトとは限りません。これは，コンパクト空間の直積が常にコンパクトであるというチコノフの定理とは対照的です。
証明
(U_n)_{n\in\mathbb{N}} を可算開被覆とする。有限集合 F\subset \mathbb{N} に対し，
V_F=\left\{ y\in Y\middle| X\times \{y\} \subset \bigcup_{n\in F} U_n\right\}
とすると， V_F は Y における開集合である。実際， y\in V_F とすると， X\times \{y\} は U_n に含まれる有限個の開長方形で覆われるからである。
X\times \{y\}\subset X\times Y はコンパクト集合より，ある部分集合 F\subset \mathbb{N} があって，X\times \{y\} \subset \bigcup_{n\in F}U_n すなわち y\in V_F とできる。よって特に， (V_F)_{F\subset \mathbb{N}; \,F\text{ is finite}} は Y の可算開被覆である。
Y は可算コンパクトより，有限部分被覆 V_{F_1}, \ldots, V_{F_m} が存在する。このとき，
X\times Y= \bigcup_{k=1}^m \bigcup_{n\in F_k} U_n
であり，右辺は有限和であるから， X\times Y は可算コンパクトである。
証明終
可算コンパクトの具体例
例1( I ).
I=[0,1] はコンパクトかつ点列コンパクトである。よって可算コンパクトである。
I がコンパクトであることはハイネ–ボレルの被覆定理とその証明～有界閉区間のコンパクト性～，点列コンパクトであることはボルツァノ–ワイエルシュトラスの定理とその証明を確認してください。
以下で解説しています。
例3(順序位相 \omega_1=[0,\omega_1) ).
\omega_1 を最小の非可算順序数とする。このとき， \omega_1=[0,\omega_1) は点列コンパクトなので可算コンパクトであるが，コンパクトでない。
なお，[0,\omega_1)\subset [0,\omega_1] とみると， [0,\omega_1) は閉集合でないですが，可算コンパクトです。ハウスドルフ空間( T_2 空間)におけるコンパクト集合は常に閉集合ですが，可算コンパクト集合はそうとは限りません。
順序位相については，以下でも解説しています。
例4( \omega_1\times I^I ).
直積位相 \omega_1\times I^I は可算コンパクト空間とコンパクト空間の直積なので，定理8より可算コンパクトである。しかし，コンパクトでも点列コンパクトでもない。
\omega_1 がコンパクトでないし， I^I は点列コンパクトでないので， \omega_1\times I^I はコンパクトでも点列コンパクトでもないです。
例5.
非可算集合 X に離散位相を入れ，かつ \{0,1\} に密着位相を入れたとする。このときの直積 X\times \{0,1\} は，極限点コンパクト(弱可算コンパクト)だが，可算コンパクトではない。
任意の空でない集合 A\subset X\times\{0,1\} に対し， (a,0)\in A ならこの開近傍には必ず (a,1) が入るし， (a,1)\in A ならこの開近傍には必ず (a,0) が入るので，極限点コンパクトがいえます。
コンパクトに関連する概念
| 名称 | 定義 |
|---|---|
| コンパクト (compact) | 任意の開被覆が有限部分被覆をもつ |
| 局所コンパクト (locally compact) | 任意の点がコンパクトな近傍をもつ |
| 強局所コンパクト (strong locally compact) | 任意の点がコンパクトな閉近傍をもつ |
| 相対コンパクト (relatively compact) | 閉包がコンパクトな部分集合 |
| 可算コンパクト (countably compact) | 任意の可算開被覆が有限部分被覆をもつ |
| リンデレーフ (Lindelöf) | 任意の開被覆が可算部分被覆をもつ |
| 点列コンパクト (sequentially compact) | 任意の点列が収束部分列をもつ |
| 極限点コンパクト (limit point compact) | 任意の無限部分集合が集積点をもつ |
| 擬コンパクト (pseudocompact) | この上の任意の実連続関数が有界 |
| σコンパクト (σ-compact) | コンパクト集合の可算和でかける空間 |
| メタコンパクト (metacompact) | 任意の開被覆が点有限な(すなわち，各点ごとに有限個の集合でしか覆われていない)開細分被覆をもつ |
| パラコンパクト (paracompact) | 任意の開被覆が局所有限な(すなわち，各点ごとに有限個の集合でしか覆われていない近傍をもつような)開細分被覆をもつ |
