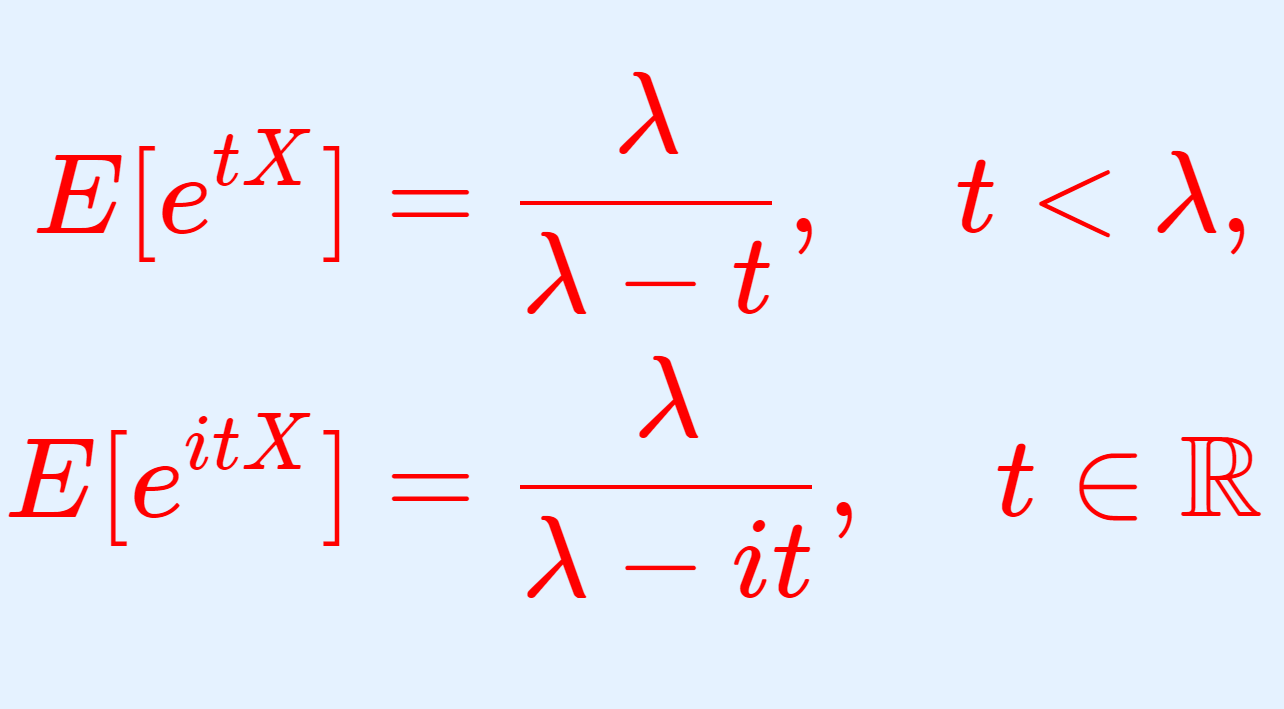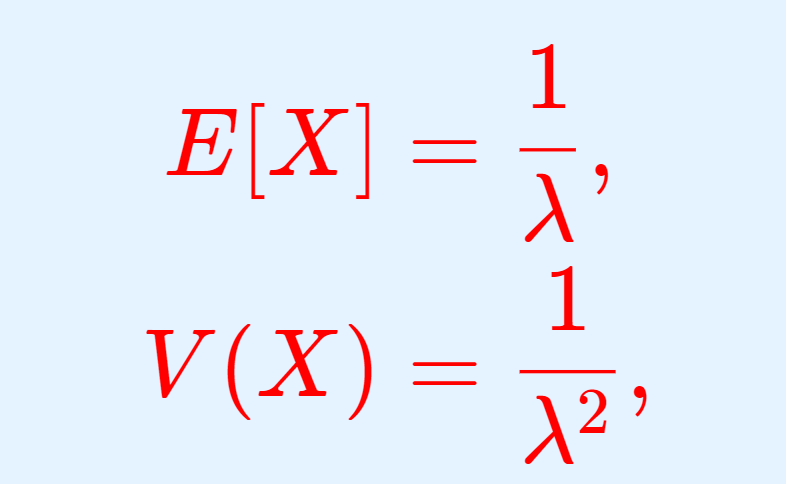指数分布において,その積率母関数(モーメント母関数)・特性関数は
\begin{aligned}E[e^{tX}]&=\frac{\lambda}{\lambda-t}, \quad t<\lambda, \\ E[e^{itX}]&=\frac{\lambda}{\lambda-it}, \quad t\in\mathbb{R} \end{aligned}
となります。これについて,導出の証明を行いましょう。
指数分布の積率母関数・特性関数
定理(指数分布の積率母関数・特性関数)
X \sim \operatorname{Exp}(\lambda) とするとき, X の積率母関数・特性関数は,それぞれ
\color{red}\begin{aligned}E[e^{tX}]&=\frac{\lambda}{\lambda-t}, \quad t<\lambda, \\ E[e^{itX}]&=\frac{\lambda}{\lambda-it}, \quad t\in\mathbb{R} \end{aligned}
である。
積率母関数・特性関数はそれぞれラプラス変換・フーリエ変換に対応しています。
証明に入る前に,指数分布の定義をおさらいしておきましょう。以下がその定義です。
指数分布の定義
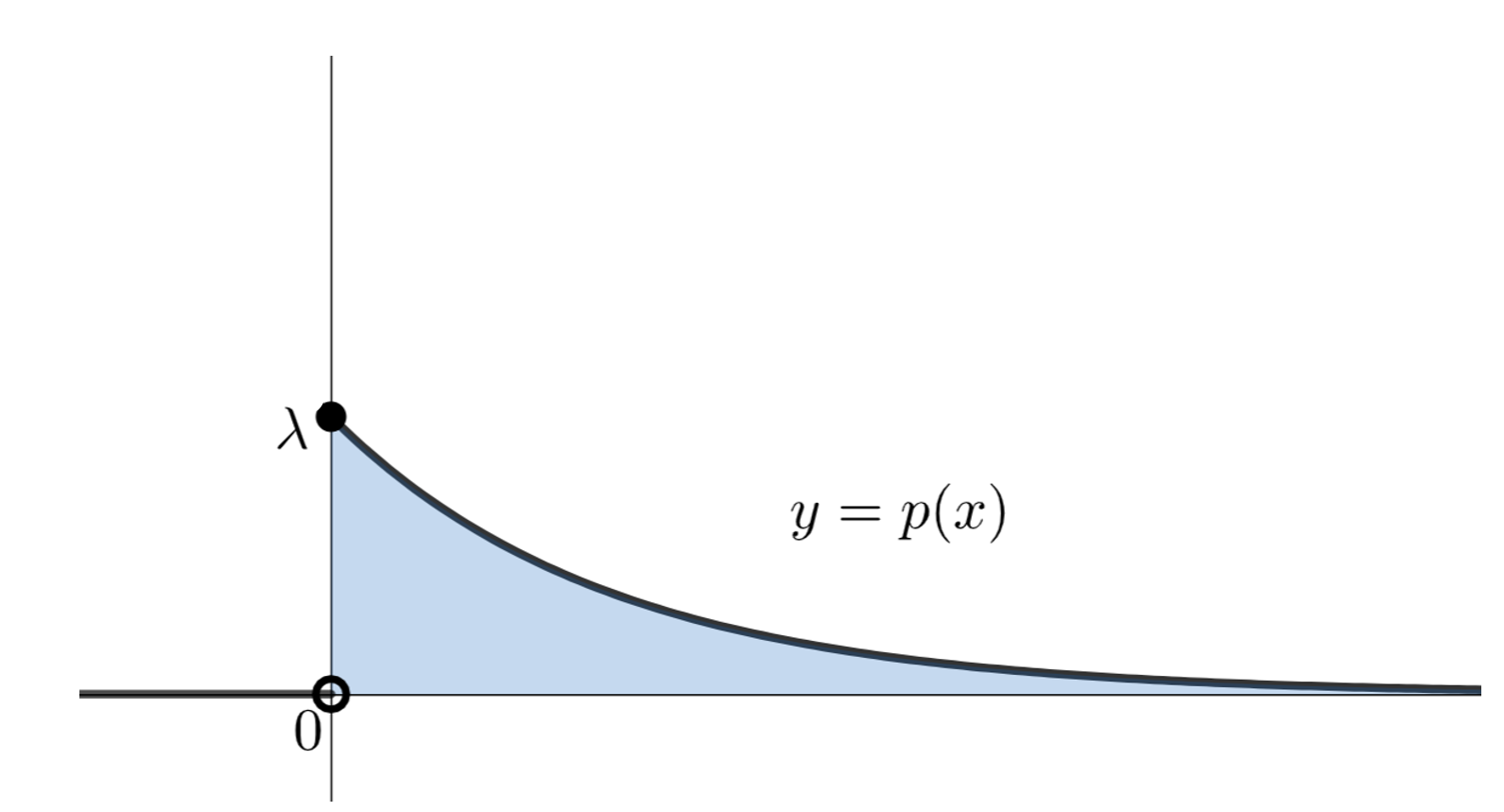
\lambda > 0 とする。確率変数 X の確率密度関数が
p(x) = \begin{cases} \lambda e^{-\lambda x } & x\ge 0,\\ 0 & x<0 \end{cases}
となるとき,X は,パラメータ \lambda の指数分布 (exponential distribution) に従うといい, X\sim \operatorname{Exp}(\lambda ) と表す。
指数分布の定義やその性質まとめについて,詳しくは,以下の記事を参照してください。
指数分布の積率母関数・特性関数の導出証明
上の定義を踏まえて,積率母関数・特性関数の導出証明を行っていきましょう。
【指数分布】積率母関数の導出
まずは積率母関数の導出です。
積率母関数の証明
\begin{aligned} E[e^{tX}] &= \int_{-\infty}^\infty e^{tx} p(x)\, dx \\ &= \int_0^\infty e^{tx}\lambda e^{-\lambda x} \, dx \\ &= \lambda \int_0^\infty e^{(t-\lambda)x}\, dx \end{aligned}
であるから, t< \lambda のときは可積分であり,
証明終
【指数分布】特性関数の導出
特性関数の導出は,積率母関数とほぼ同様に思えるかもしれません。
特性関数の証明
\begin{aligned} E[e^{itX}] &= \int_{-\infty}^\infty e^{itx} p(x)\, dx \\ &= \int_0^\infty e^{itx}\lambda e^{-\lambda x} \, dx \\ &= \lambda \int_0^\infty e^{(it-\lambda)x}\, dx \\ &= \frac{\lambda}{\lambda-it}. \end{aligned}
であるから,証明が終わる。
証明終