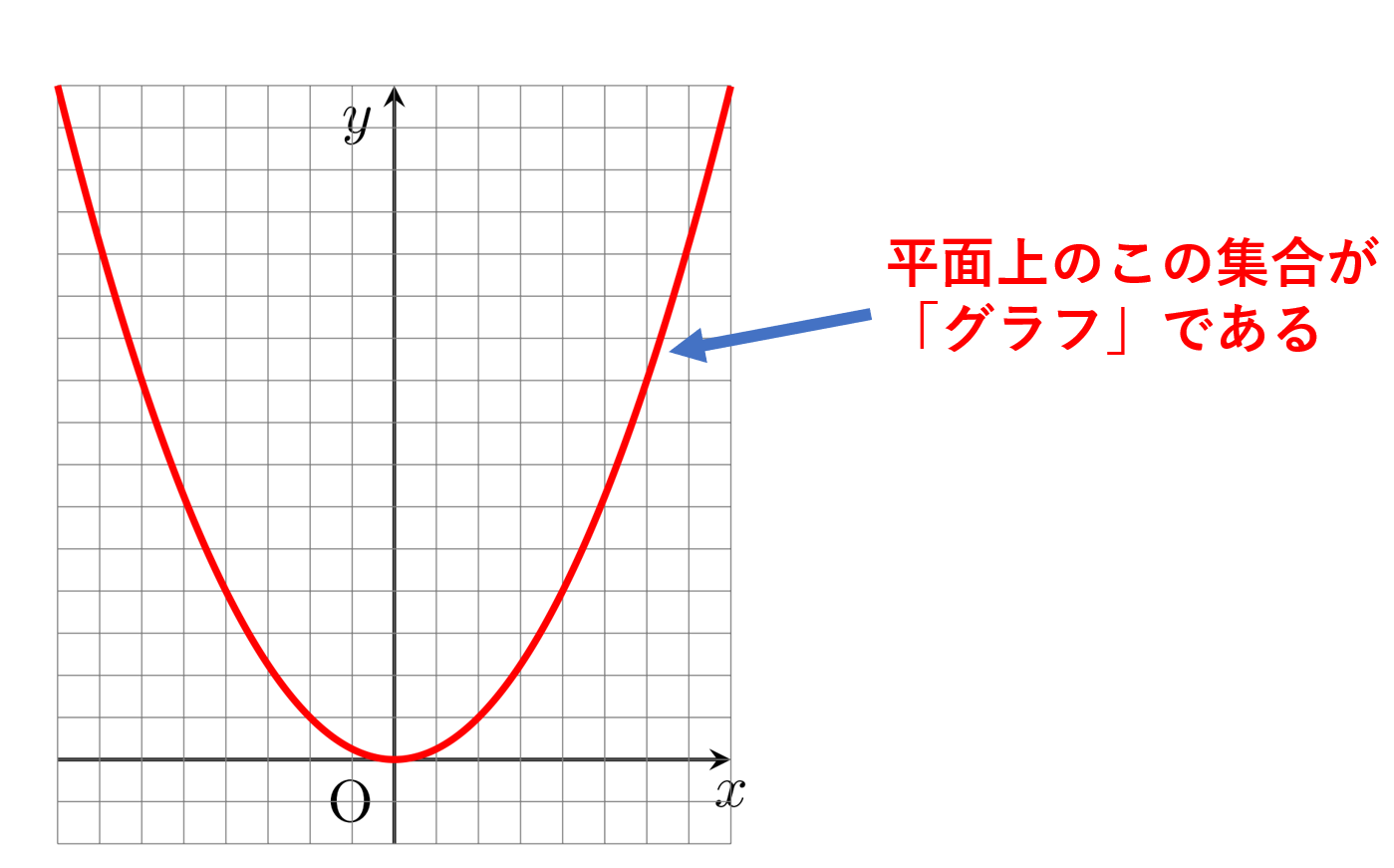
関数(写像)の「グラフ」とは何かを厳密に定義しよう

関数(写像)の「グラフ」というと， $xy$ 平面上の「図」を思い浮かべる人も多いのではないでしょうか。実際，一般の関数において，関数の「グラフ」とはどう定義されるかについて紹介します。

関数(写像)の「グラフ」の定義

定義（関数・写像のグラフ）

一般に， $f\colon X \to Y$ に対し，集合

\textcolor{red}{G(f) = \{(x, f(x)) \in X \times Y \mid x \in X\} }

を $f$ のグラフ (graph) という。

グラフとは $(x, f(x))$ 組の集合だと言っています。

例

$f\colon \mathbb{R} \to \mathbb{R}$ を $f(x)=x^2$ とする。
このとき， $f$ のグラフは，集合

\{ (x,x^2) \in \mathbb{R}^2 \mid x \in \mathbb{R} \}

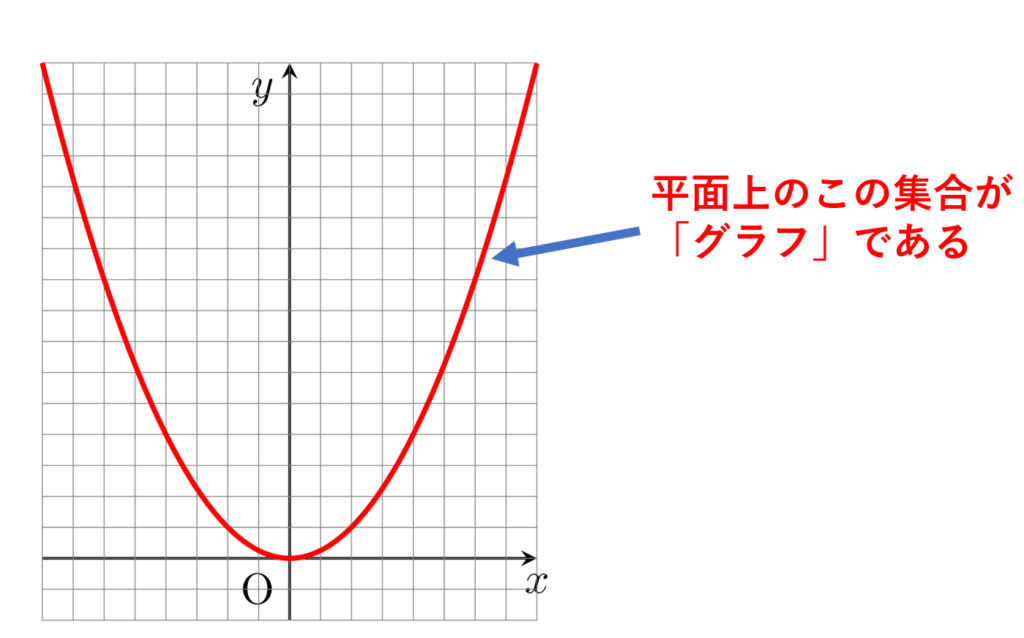
である。

グラフとは集合だということを知っておきましょう。