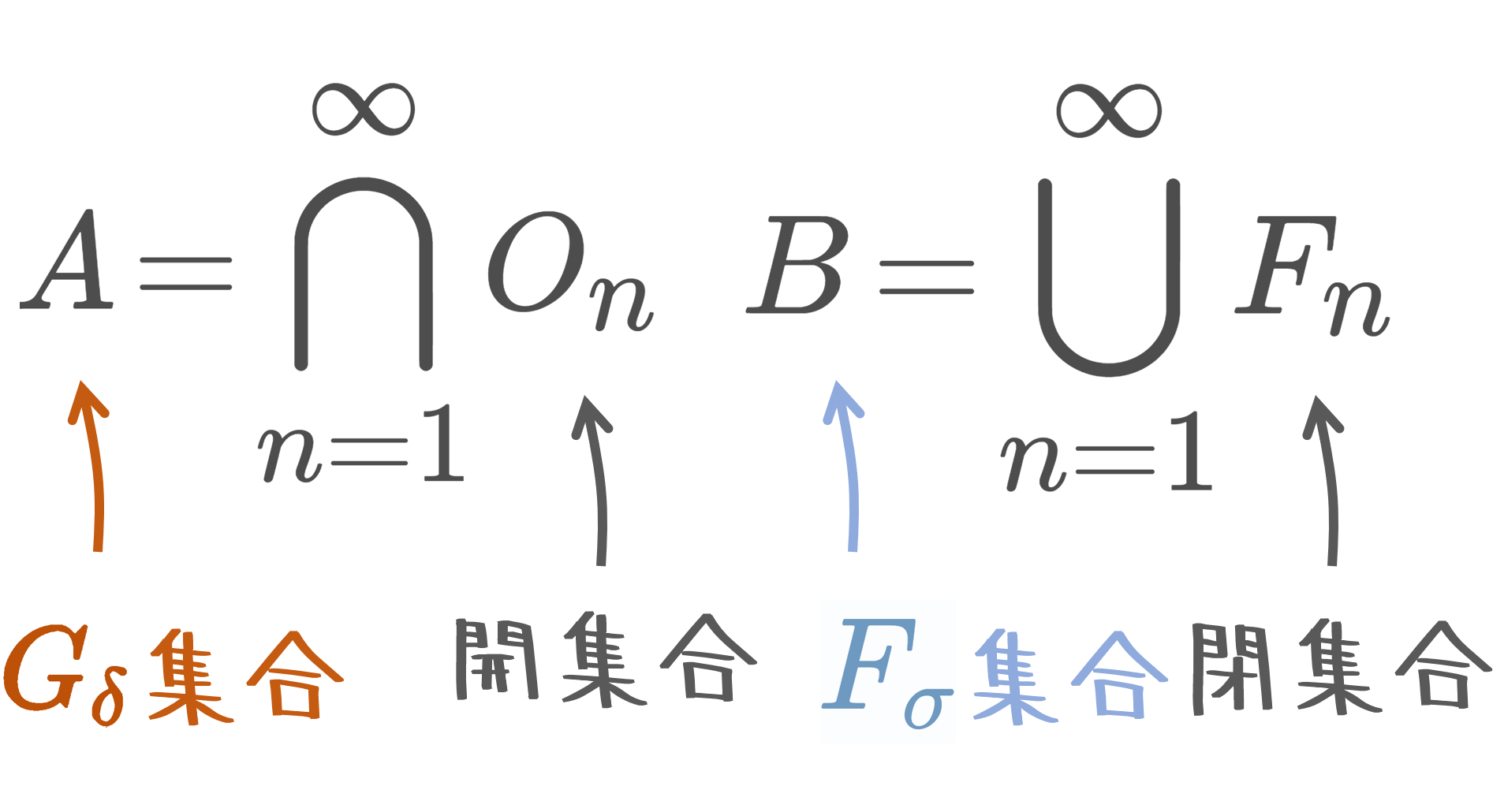Gδ集合とは,開集合の可算個の共通部分で表せるような集合のことで,Fσ集合は,閉集合の可算和で表せるような集合のことです。Gδ集合・Fσ集合は互いに補集合の関係になっています。
Gδ集合・Fσ集合について,その定義と具体例を紹介し,さらに,実数値関数の連続点にまつわる面白い定理を紹介しましょう。
Gδ集合・Fσ集合の定義
定義(Gδ集合・Fσ集合)
(X,\mathcal{O}) を \mathcal{O} を開集合族とする位相空間とし,\mathcal{F} を (X,\mathcal{O}) の閉集合族とする。
部分集合 A\subset X に対し,ある開集合の列 \{O_n\}\subset \mathcal{O} が存在して,
\Large\color{red} A = \bigcap_{n=1}^\infty O_n
と表せるとき, A を G_\delta 集合 ( G_\delta set)という。
部分集合 B\subset X に対し,ある閉集合の列 \{F_n\}\subset \mathcal{F} が存在して,
\Large\color{red} B = \bigcup_{n=1}^\infty F_n
と表せるとき, B を F_\sigma 集合 ( F_\sigma set) という。
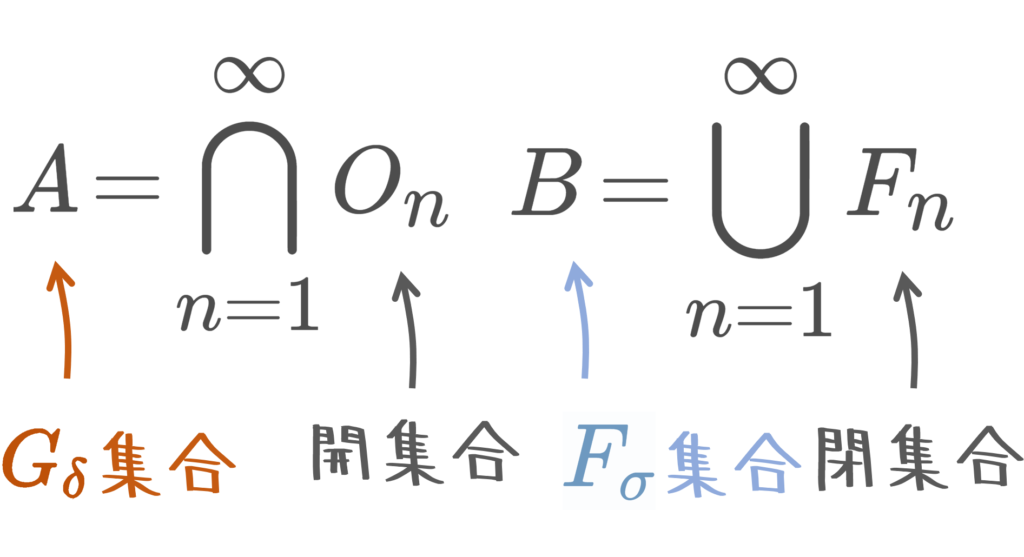
開集合の可算交叉で表せる集合が G_\delta 集合で,閉集合の可算和で表せるのが F_\sigma 集合です。
定義より,開集合 \implies G_\delta 集合だし,閉集合 \implies F_\sigma 集合ですが,逆は成立しません。開集合は,有限交叉と無限個の和で閉じていますが,可算交叉では閉じていないので, G_\delta 集合は開集合とは限りません。同じく,閉集合は有限和と無限個の交叉で閉じていますが,可算和では閉じていないので, F_\sigma 集合は閉集合とは限りません。
また定義とド・モルガンの法則により,明らかに G_\delta 集合の補集合は F_\sigma 集合で, F_\sigma 集合の補集合は G_\delta 集合です。
Gδ集合・Fσ集合の具体例
例1(\R).
実数全体の集合 \R の通常の位相について,
- 有理数全体の集合 \mathbb{Q} は F_\sigma 集合だが G_\delta 集合ではない。
- 無理数全体の集合 \R\setminus \mathbb{Q} は G_\delta 集合だが F_\sigma 集合ではない。
\mathbb{Q} は可算集合なのと,\mathbb{Q}=\bigcup_{q\in\mathbb{Q}} \{q\} より,\mathbb{Q} は F_\sigma 集合です。同様に, \R\setminus \mathbb{Q}=\bigcap_{q\in\mathbb{Q}} (\R\setminus \{q\}) より, \R\setminus \mathbb{Q} は G_\delta 集合です。
\mathbb{Q} が G_\delta 集合でないこと・\R\setminus \mathbb{Q} が F_\sigma 集合でないことを示すのは,ベールのカテゴリー定理 (Baire’s category theorem) が必要です。
完備距離空間において,稠密 (dense) な開集合の可算族 \{U_n\} の共通部分 \bigcap_{n=1}^\infty U_n もまた稠密 (dense) である。
\R は完備距離空間なので,もし,\mathbb{Q} が G_\delta 集合だとすると,おかしいです。実際,\mathbb{Q} が G_\delta 集合として, \mathbb{Q}=\bigcap_{n=1}^\infty O_n ( O_n は開集合)とかけたとすると,\mathbb{Q} は稠密なので, \mathbb{Q}\subset O_n をみたす各 O_n は当然稠密です。すると,ベールのカテゴリー定理により,
\Bigl(\bigcap_{n=1}^\infty O_n \Bigr)\cap \Bigl(\bigcap_{q\in\mathbb{Q}} (\R\setminus \{q\}) \Bigr) =\mathbb{Q}\cap (\R\setminus \mathbb{Q})=\emptyset
も稠密になるはずですが,なっていないので矛盾しています。ゆえに,\mathbb{Q} は G_\delta 集合ではありません。補集合を考えると, \R\setminus \mathbb{Q} は F_\sigma 集合ではありません。
A\subset X を閉集合とすると,開集合 O_n=\{ x\in X\mid d(x, A)<1/n\} によって, A=\bigcap_{n=1}^\infty O_n と表せるので, A は G_\delta 集合です。補集合を考えることで,後半も言えます。
例3(補有限位相).
X を空でない集合とする。
\mathcal{O}_f=\{\emptyset\}\cup \{ O\subset X\mid X\setminus O \text{ is finite}\}
を,補集合が有限集合である部分集合全体(と \{\emptyset\} との和集合)とすると, (X,\mathcal{O}_f) は位相空間になる。この位相を補有限位相 (cofinite topology, finite complement topology) という。
自分で考えてみてください。
補有限位相の性質については,以下で詳しく解説しています。
Gδ集合の面白い性質
G_\delta 集合にまつわる面白い定理を一つ紹介しましょう。
定理(連続点は G_\delta 集合)
関数 f\colon \R\to \R における連続点全体の集合を
C_f=\{ c\in \R\mid \lim_{x\to c} f(x)=f(c)\}
とする。このとき, C_f は \R における G_\delta 集合である。
逆に, C\subset \R を G_\delta 集合とするとき,関数 f\colon \R\to \R で C_f=C となるものが存在する。
この定理と例2.から,有理数で不連続・無理数で連続な関数は作れますが,その逆で,無理数で不連続・有理数で連続な関数は作れないことが分かります。有理数で不連続・無理数で連続な関数はトマエ関数 (Tomae function) が有名です。トマエ関数とは,
f(x) = \begin{dcases} 1/p & x = q/p \;\; (p\ge 1, \, \operatorname{gcd}(p,q)=1), \\ 0 & x \in \mathbb{R}\setminus\mathbb{Q}, \\ 1 & x=0\end{dcases}
をみたす関数のことです。以下で解説しています。
定理を証明しましょう。
定理の証明
前半について
開集合 U\subset \R に対し,
\operatorname{diam } f(U)=\sup_{x,y\in U} |f(x)-f(y)|
を,像 f(U) の直径 (diameter) とする。 \R の開集合族を \mathcal{O} とすると,
であることを示そう。 c\in C_f とすると,連続の定義より,任意の n\ge 1 に対し,ある開近傍 (c\in) U\in \mathcal{O} が存在して,y\in U\implies |f(y)-f(c)|\le 1/(2n) とできる。このとき, x,y\in U に対し,
なので, \operatorname{diam}f(U)\le 1/n となる。よって, c \in \bigcap_{n=1}^\infty ( \bigcup_{\substack{U\in\mathcal{O} \\ \operatorname{diam} f(U)\le 1/n}} U) である。
逆に, c\in \bigcap_{n=1}^\infty ( \bigcup_{\substack{U\in\mathcal{O} \\ \operatorname{diam} f(U)\le 1/n}} U) とすると,任意の n\ge 1 に対し,ある U\in\mathcal{O} が存在して, c\in U かつ \operatorname{diam} f(U)\le 1/n とできる。ゆえに,任意の n\ge 1 に対し,ある開近傍 (c\in )U\in\mathcal{O} が存在して,
x\in U\implies |f(x)-f(c)|\le \frac{1}{n}
となるが,これは連続の定義そのものであるから, c\in C_f である。ゆえに赤字の式が示せた。赤字の式は, C_f が G_\delta 集合であることを示している。
後半について
C を G_\delta 集合とすると,開集合族 \{O_n\}\subset\mathcal{O} に対し, C = \bigcap_{n=1}^\infty O_n と表せる。
U_0=\R,\quad U_n =\bigcap_{k=1}^n O_k
と定めると, U_n は開集合で, U_0\supset U_1\supset U_2\cdots かつ C=\bigcap_{n=0}^\infty U_n である。 n=0,1,2,\ldots に対し, V_n = U_n\setminus U_{n+1} とおくと, \{V_n\} はどの2つも共通部分をもたず, \R\setminus C=\bigsqcup_{n=0}^\infty V_n である。ただし, \bigsqcup は非交和を表す。さらに W_n = V_n\setminus \bigl(\operatorname{Int}(V_n)\cap \mathbb{Q}\bigr) とする。ただし, \operatorname{Int}(V_n) は V_n の内部(開核)である。 W_n\subset V_n より, \{W_n\} もどの2つも共通部分をもたない。
とすると,これが目的の関数であることを示そう。 x\in \R\setminus C=\bigsqcup_{n=0}^\infty V_n とする。このとき,唯一つの n\ge 1 が存在して, x\in V_n とできる。 x\in \operatorname{Int}(V_n)\cap \mathbb{Q} のとき, f(x)=0 となる。 x\in \operatorname{Int} (V_n) より,ある \delta >0 が存在して, (x-\delta, x+\delta) \subset V_n とできる。ゆえに,任意の \varepsilon >0 で (x-\varepsilon, x+\varepsilon )\cap W_n\ne \emptyset なので, x \notin C_f である。また, x\in W_n のときは, f(x)=1/n となるが,ある \delta >0 について (x-\delta, x+\delta ) \subset V_n となるとき,任意の \varepsilon>0 で (x-\varepsilon, x+\varepsilon )\cap ( \operatorname{Int}(V_n)\cap \mathbb{Q})\ne \emptyset となるので, x\notin C_f である。また,そのような \delta が存在しないときは, x\notin \operatorname{Int}(V_n) なので,任意の \varepsilon>0 について (x-\varepsilon, x+\varepsilon )\cap V_i\ne\emptyset となる i\ne n が存在し, V_i 上では f(y)=0\text{ or } 1/i \ne 1/n なので,やはり x\notin C_f である。
x\in C = \bigcap_{n=0}^\infty U_n とする。このとき,x はどの V_n にも入らないので, f(x)=0 である。 x\in \cdots \subset U_2\subset U_1\subset U_0 なので,任意の n\ge 1 について, U_n は x の開近傍であり, U_n = U_{n+1}\sqcup V_n = C\sqcup (\bigsqcup_{k=n}^\infty V_k) なので, y\in U_n\implies |f(y)-f(x)|=|f(y)|\le 1/n とできる。したがって, x\in C_f である。
以上から, C_f=C が示された。
証明終
後半の関数の構成方法は,トマエ関数のときと似ていますね。