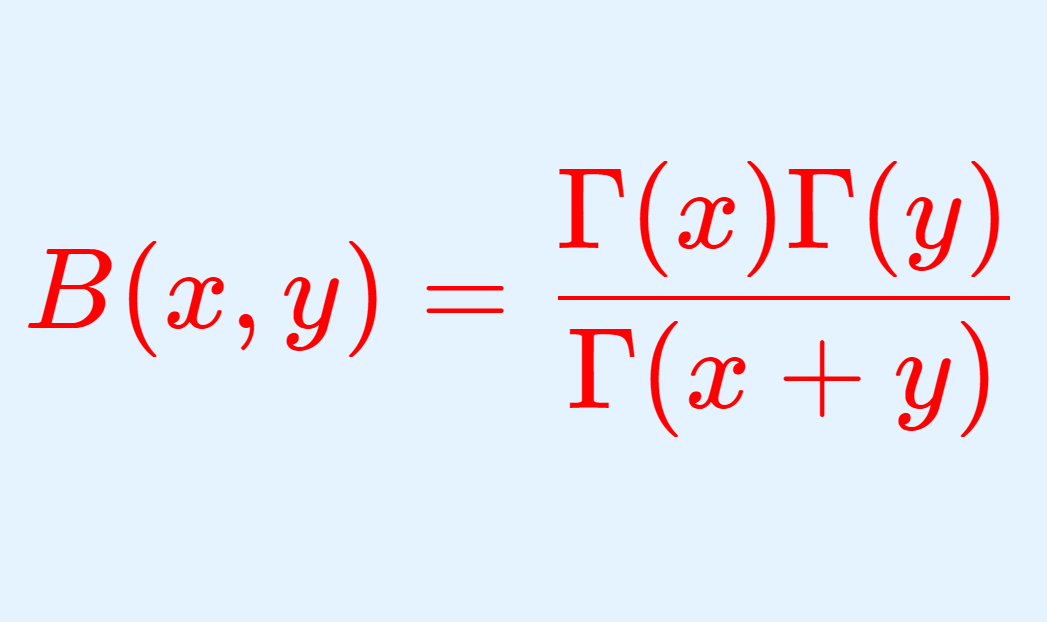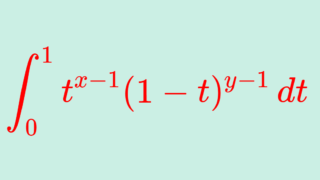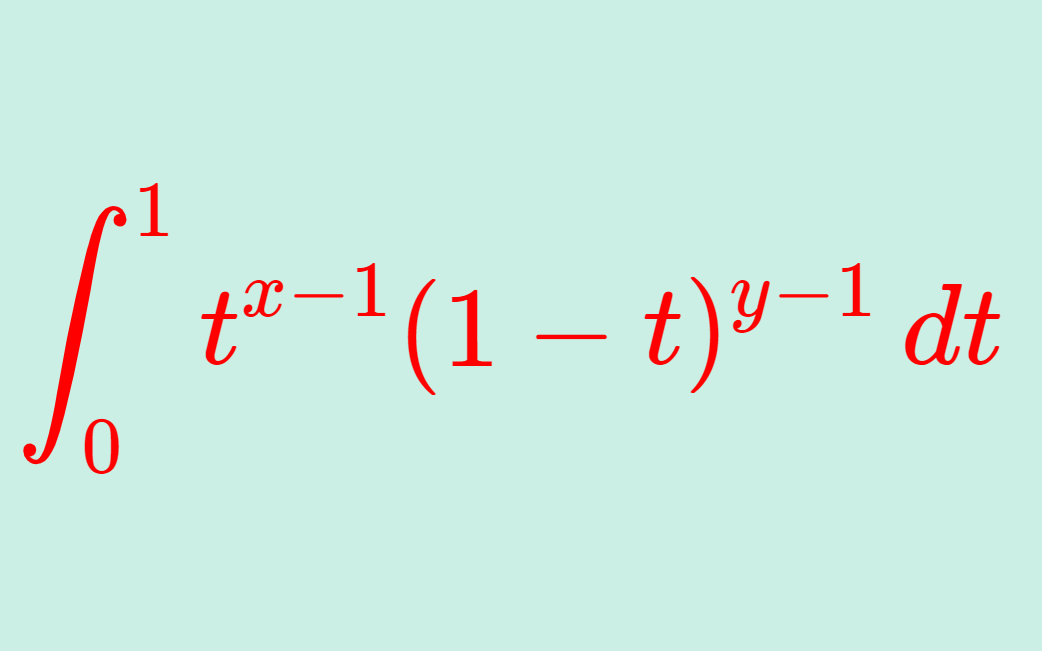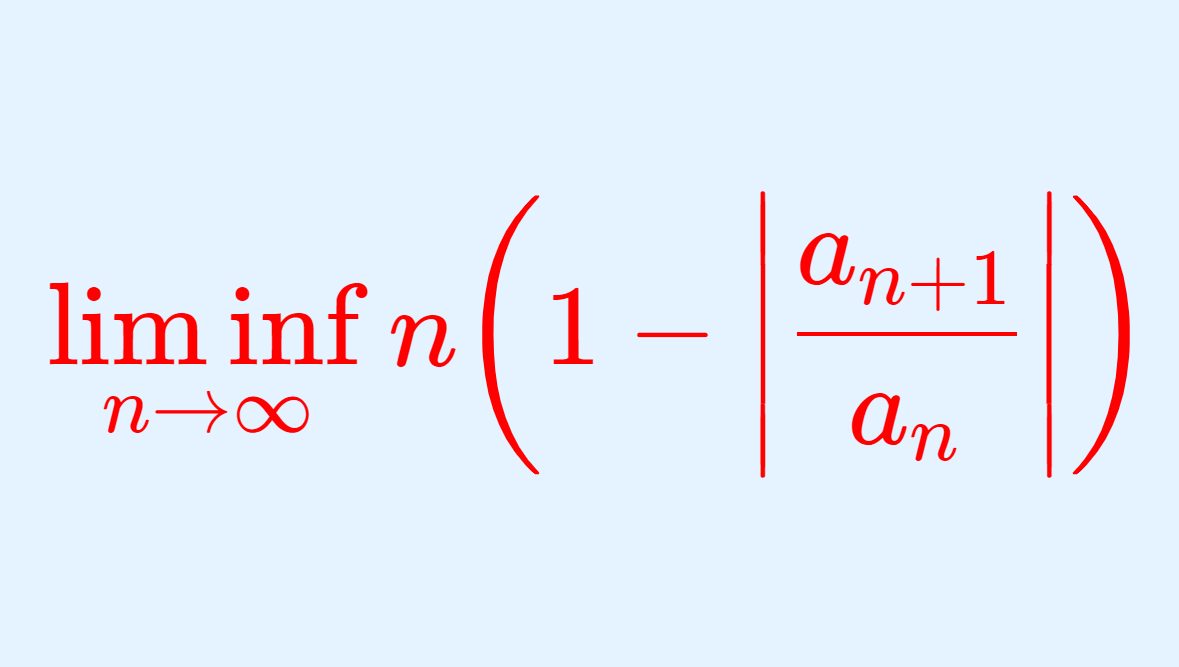ガンマ関数とベータ関数の関係式とその証明

B(x,y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}

という関係式があります。これについて，その導出の証明を行いましょう。

ガンマ関数とベータ関数の関係式

定理（ガンマ関数とベータ関数の関係）

$\operatorname{Re} x, \,\operatorname{Re} y > 0$ とする。このとき，

\color{red}B(x,y) = \frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}

である。ただし，

\begin{aligned}\Gamma(x) &= \int_0^\infty t^{x-1}e^{-t}\, dt, \\ B(x,y) &=\int_0^1 t^{x-1} (1-t)^{y-1}\, dt \end{aligned}

重積分における変数変換の知識があれば，証明はついてこれるでしょう。早速証明します。

重積分の変数変換については，以下で解説しています。

証明

ガンマ関数の定義より，

\begin{aligned}\Gamma(x) \Gamma(y) &= \int_0^\infty s^{x-1}e^{-s}\,ds \int_0^\infty t^{y-1}e^{-t}\, dt \\ &=\int_0^\infty\int_0^\infty s^{x-1}t^{y-1}e^{-s-t}\,dsdt. \end{aligned}

ここで， $s=uv,\, t=u(1-v)$ と置換積分する。

$\{(s,t)\mid s,t\in (0,\infty)\} = \{(uv, u(1-v))\mid u\in(0,\infty), v\in (0,1)\}$ ，

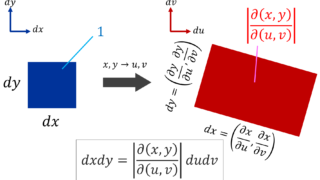
\begin{aligned} dsdt &= \left| \det\begin{pmatrix}\partial s/\partial u & \partial s/\partial v \\ \partial t/\partial u & \partial t/\partial v\end{pmatrix}\right|dudv \\ &= \left|\det\begin{pmatrix} v&u \\ 1-v & -u \end{pmatrix}\right| dudv \\ &= ududv\end{aligned}

であることに注意すると，

\begin{aligned}&\Gamma(x)\Gamma(y) \\ &= \int_0^\infty \int_0^1 e^{-u} (uv)^{x-1}(u(1-v))^{y-1}\, udvdu \\ &= \int_0^\infty \int_0^1 e^{-u} u^{x+y-1} v^{x-1}(1-v)^{y-1}\, dvdu \\ &= \int_0^\infty e^{-u}u^{x+y-1}\, du\int_0^1 v^{x-1}(1-v)^{y-1}\, dv\\ &= \Gamma(x+y)B(x,y) \end{aligned}

である。したがって， $B(x,y) =\dfrac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}.$

証明終

無事証明できましたね。厳密には複素数値重積分ですが，積分区間は実数のため，単に $\operatorname{Re} ,\operatorname{Im}$ に分ければ，実数値重積分に帰着されます。問題ないでしょう。