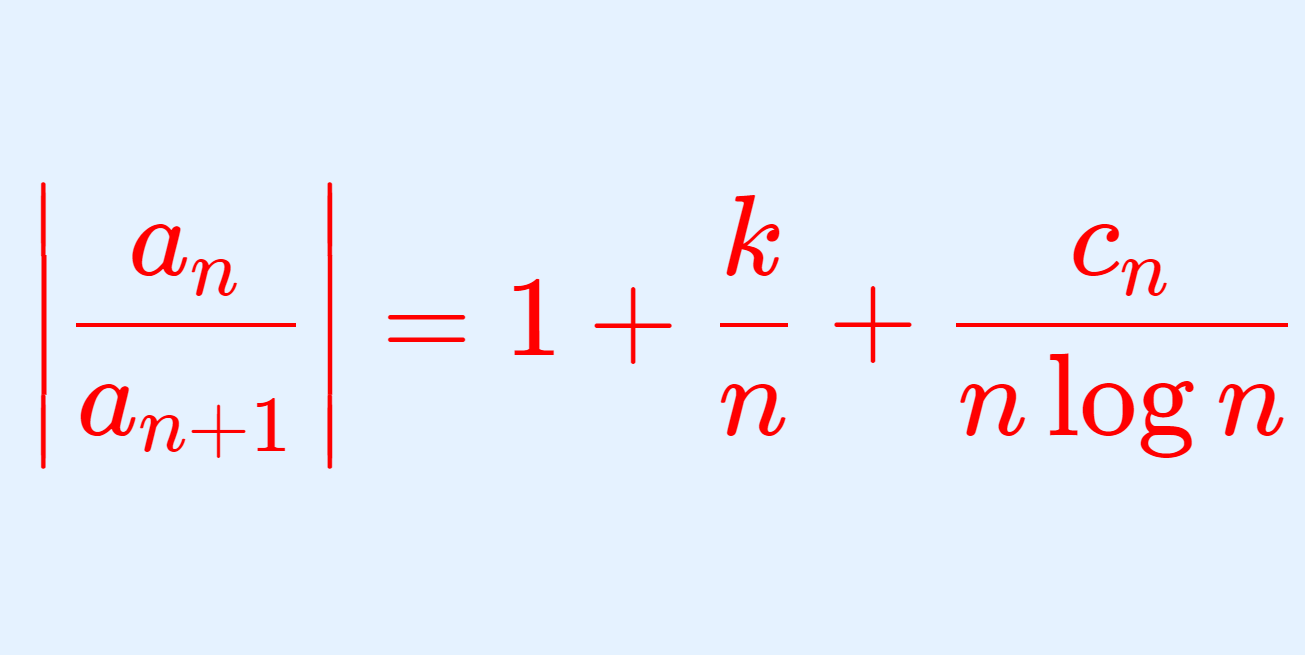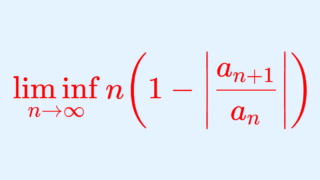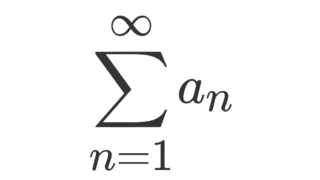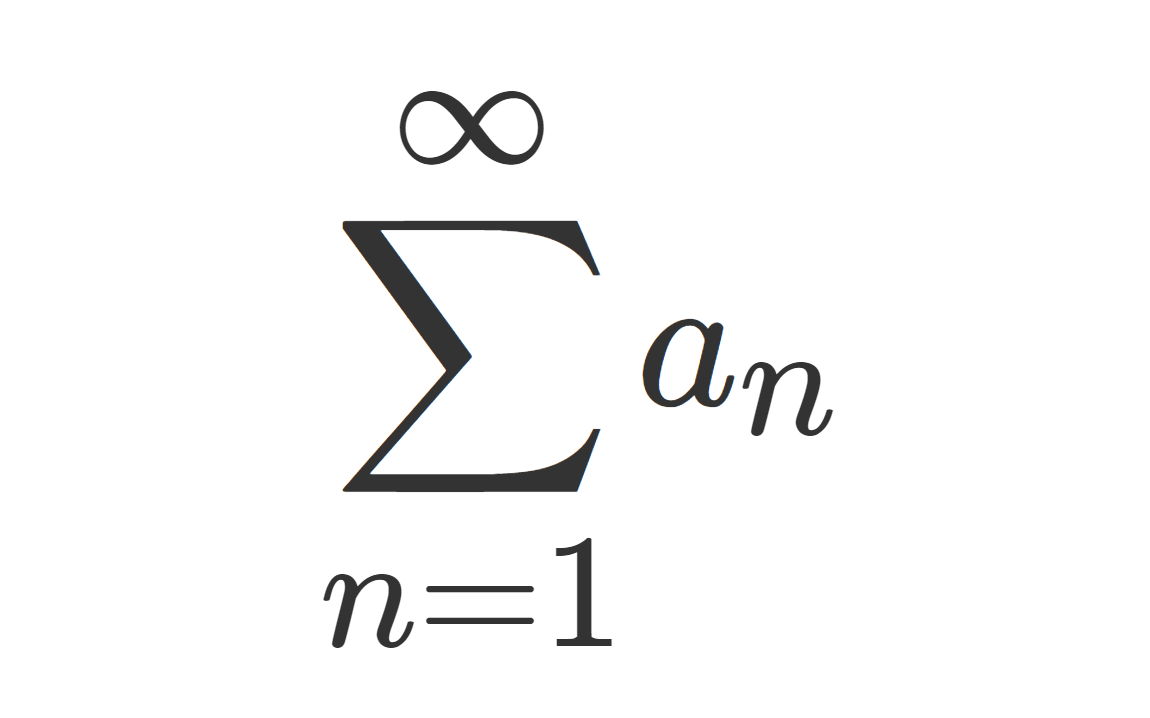ガウスの収束判定法とは,級数 \sum_{n=1}^\infty a_n の収束判定法の1つで, \lim_{n\to\infty} |a_n/a_{n+1}|=1 となってダランベールの収束判定法が使えないときに有用な収束判定法の1つです。これについて,その主張と具体例,証明を紹介しましょう。
【級数の収束判定法】ガウスの判定法とは
定理(ガウスの判定法; Gauss’s test)
0 にならない数列 \{ a_n\} に対し, c_n \xrightarrow{n\to\infty}0 となる,ある数列 \{c_n\} を用いて,
\color{red} \left| \frac{a_n}{a_{n+1}}\right| = 1+\frac{k}{n} + \frac{c_n}{n \log n}
と表せるとする。このとき, \sum_{n=1}^\infty a_n について
- \color{red} k > 1 ならば絶対収束し,
- \color{red} k \le 1 ならば条件収束または発散する(正項級数 a_n > 0 ならば発散する)。
今回は
\left| \frac{a_n}{a_{n+1}}\right| = 1+\frac{k}{n} + \frac{c_n}{n \log n}
を採用しましたが,これは,ランダウの記号を用いると,
とかけます。他に,ガウスの収束判定法は a_n/a_{n+1} の代わりにその逆数 a_{n+1}/a_n を考えて,
とかいても同じです。
さらに,ガウスの収束判定法は,ある \alpha > 0 を用いて,
\color{red} \left| \frac{a_n}{a_{n+1}}\right| = 1+\frac{k}{n} + O\!\left(\frac{1}{n^{1+\alpha}}\right)
とすることもあります。これは,定理にかいた形の特別な場合になっています。さまざまなかき方がある「ガウスの収束判定法」ですが,今回は,定理にかいた形を採用することにしましょう。
k の値を求めるには,
k = \lim_{n\to\infty} n\!\left( \left| \frac{a_n}{a_{n+1}}\right| - 1\right)
を計算すればよいです。ここで, k\ne1 の場合は,まさにラーベの収束判定法になっています。よって,ガウスの収束判定法を用いる必要はありません。以下で解説しています。
逆に,ガウスの収束判定法が真価を発揮するのは, k=1 の場合である,といえます。
ガウスの判定法の具体例
例1.
s,t>0 とする。\color{red} a_n = \dfrac{t(t+1)\dots(t+n-1)}{s(s+1)\dots(s+n-1)} とおいたときの \sum_{n=1}^\infty a_n の収束・発散について
\left| \frac{a_n}{a_{n+1}}\right| = 1+\frac{k}{n} + \frac{c_n}{n \log n}
に当てはめると, k=s-t,
であるから, s-t >1 のとき収束, s-t\le 1 のとき発散する。
ガウスの判定法の証明
証明は,他の収束判定法の証明に帰着させることで,行ったことにしましょう。
証明
k\ne 1 のときは,ラーベの収束判定法に帰着するため,そちらを参照するとよい。
k=1 のときは,
\left| \frac{a_n}{a_{n+1}}\right| = 1+\frac{1}{n} + \frac{c_n}{n \log n}
かつ \lim_{n\to\infty} c_n=0 となるが,これはBertrandの収束判定法に帰着する。これについては,【級数の収束判定法】Bertrand’s testとはを参照するとよい。
証明終