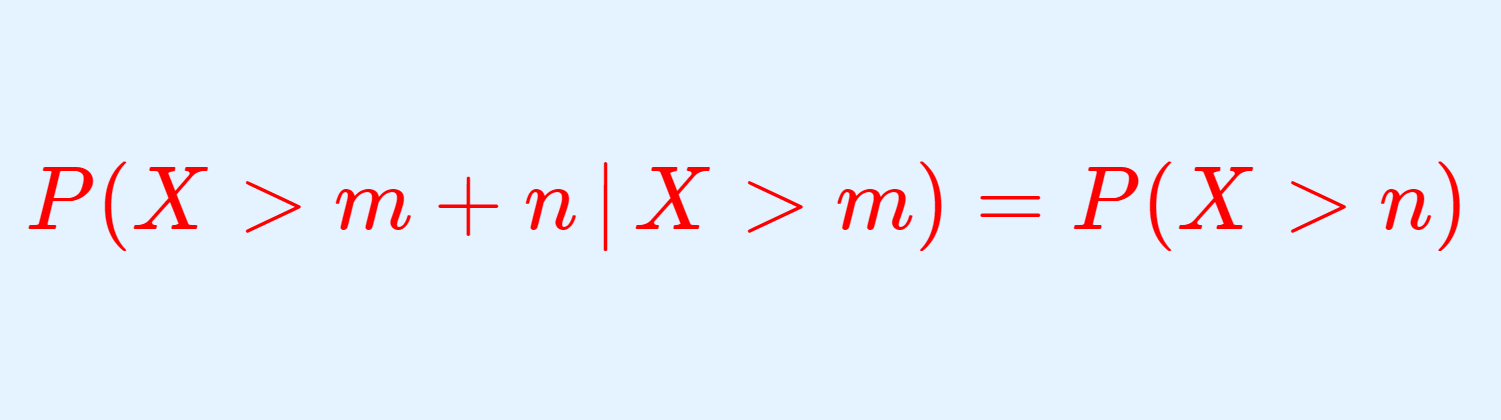幾何分布における,無記憶性と呼ばれる P(X>m+n\,|\,X>m) = P(X>n) という性質について解説し,「幾何分布が無記憶性をもつ」ことと「離散型確率分布が無記憶性をもつ場合,それは幾何分布に限る」ことの2つを証明しましょう。
幾何分布の無記憶性
定理(幾何分布の無記憶性)
X \sim \operatorname{Geo}(p) とし, m,n \ge 1 を正の整数とする。このとき,
\color{red}P(X>m+n\,|\, X>m ) =P(X>n)
である。これを無記憶性 (lack of memory property, memorylessness) という。
逆に,無記憶性をもつ離散型の確率分布は幾何分布に限る。
「無記憶性」とは,以前までの結果が後の結果に影響を与えないことを指します。幾何分布は,「コインで初めて表が出るまでにコインを投げる回数」をモデル化したものですが,たとえば, k 回目「裏」だったからと言って, k+1 回目に「表」になる確率が上がるわけではありませんね。それまでの試行は,以降の試行に関係ないわけです。
また逆に,無記憶性をもつ離散型確率分布は幾何分布に限るわけですから,離散型の確率分布で,無記憶性をもつものをモデル化したいときは,幾何分布が最適だということにもなります。
さて,上の証明に行く前に,まず幾何分布の定義を復習しておきましょう。
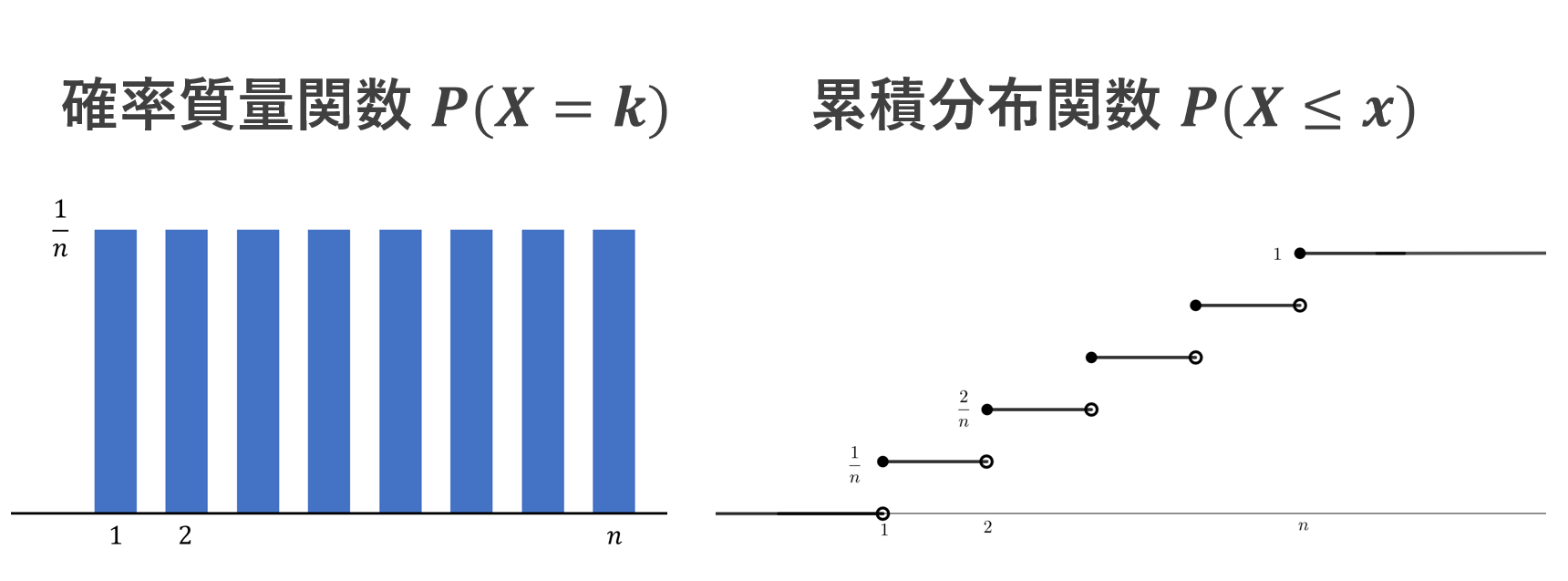
X を確率変数, 0<p<1 とする。 k=1,2,3,\ldots に対し,
\color{red} P(X=k) = (1-p)^{k-1} p
が成立するとき, X はパラメータ p の幾何分布 (geometric distribution) に従うという。本記事では,これを \color{red} X\sim \operatorname{Geo}(p) とかくことにする。
幾何分布は,離散型確率分布の1つで,「確率 p で表が出るコインを何回も振ったときに,何回目に初めて表が出るか」をモデル化したものです。幾何分布について,詳しくは以下の記事を参照してください。
幾何分布の無記憶性の証明
- 幾何分布は無記憶性をもつこと
- 無記憶性をもつ離散型確率分布は幾何分布に限ることの
の2つについて,順番に証明していきましょう。
幾何分布は無記憶性をもつこと
こちらに関しては,
\begin{aligned} P(X>m) &= \sum_{k=m+1}^\infty P(X=k) \\ &= \sum_{k=m+1}^\infty (1-p)^{k-1}p \\ &= (1-p)^m \end{aligned}
であることを踏まえれば,証明は簡単です。
証明
正の整数 m,n に対し,
\begin{aligned} P(X>m+n\,|\, X>m) &= \frac{P(X>m+n)}{P(X>m)}\\ &= \frac{(1-p)^{m+n}}{(1-p)^m} \\ &= (1-p)^n \\ &= P(X>n) \end{aligned}
であるから,無記憶性が分かる。
証明終
無記憶性をもつ離散型確率分布は幾何分布に限ること
さて,逆の証明もしていきましょう。
ここで注意ですが,「無記憶性をもつ離散型確率分布は幾何分布に限る」と言ったときの「離散型確率分布」は,正の整数値のみをとりうるものとします。 X=0.5 とかを許してしまうと,以下の証明とは,話が変わってきます。
証明
正の整数 m に対し,
P(X>m+1\, | X>1) = P(X>m)
であるから, P(X>m+1) = P(X>1)P(X>m) となる。これの繰り返しにより,
をえる。よって, q = P(X>1 ) とおくと, P(X>m) = q^m . また, P(X>0) = 1 であったから,この式は m=0 でも成立する。これにより,
q=1-p とおくと, P(X=m) = (1-p)^{m-1}p となって,これは幾何分布を表す。
証明終
なお,上の証明では正の整数値のみを許しましたが,整数値全体を許す場合について, P(X>0) > 0 のもとで無記憶性
P(X>0+0\,|\, X>0) = P(X>0)
をみたすとすると, P(X>0) = P(X>0)^2 ですから, P(X>0) =1 となって,結局 X は正の整数値のみしかとることができませんね。
なお関連して,無記憶性をもつ連続型確率分布は,指数分布に限ることが知られています。これについては,指数分布の無記憶性とその証明を参照してください。