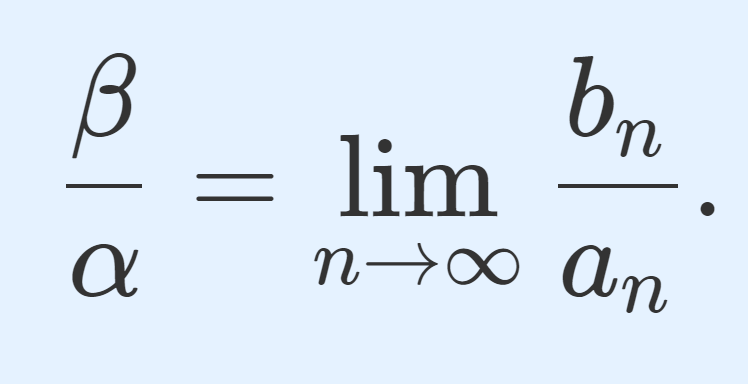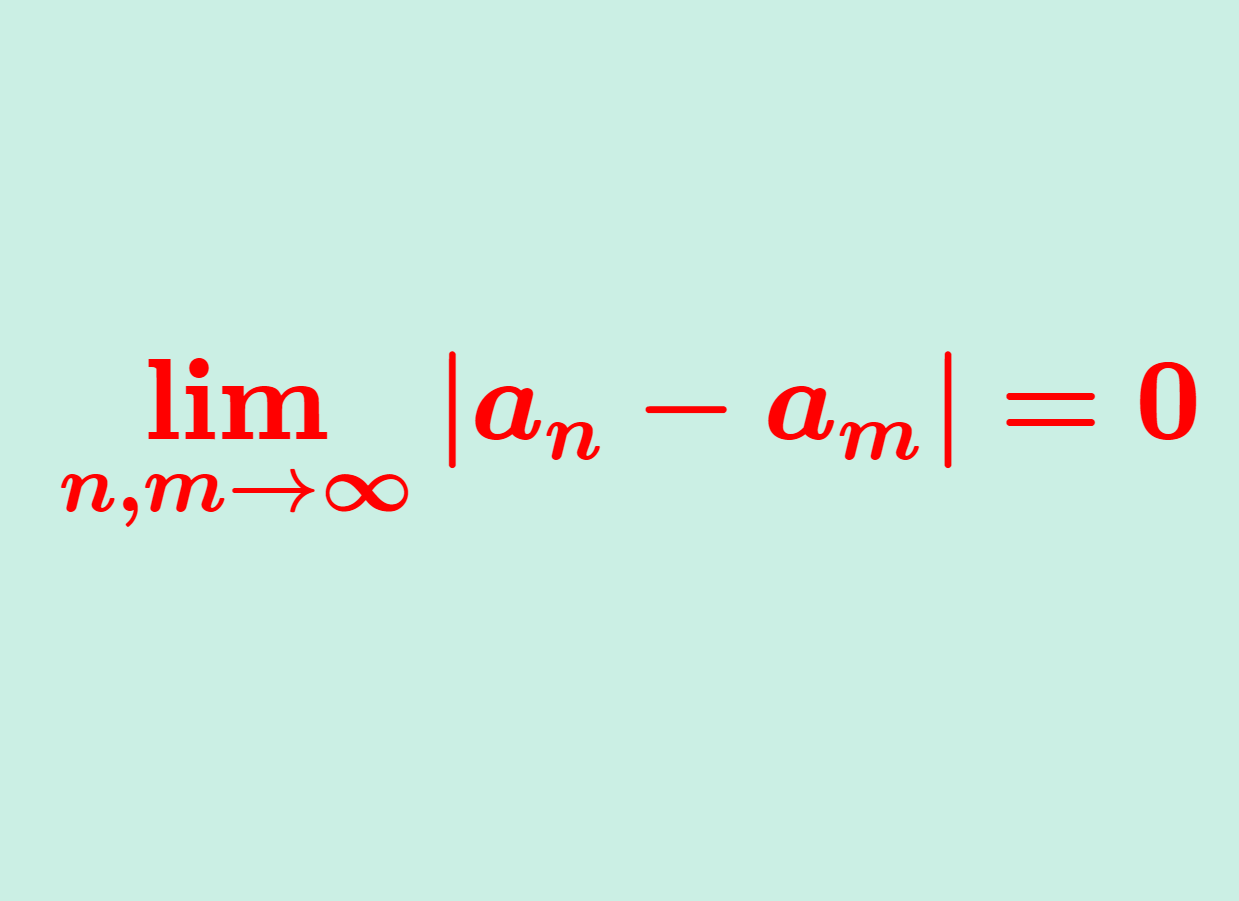極限の厳密な定義である \varepsilon\text{-}N 論法や \varepsilon\text{-}\delta 論法を踏まえて，極限の基本的な性質の証明を紹介します。
\varepsilon\text{-}N 論法や \varepsilon\text{-}\delta 論法の演習問題としても最適なので，確認していきましょう。
数列の極限を定義するイプシロンエヌ論法，関数の極限を定義するイプシロンデルタ論法については，それぞれ以下の記事で解説しています。本記事は，これらを多少なりとも既知とします。
数列の極限の基本的な性質
主張一覧
定理（数列の極限の性質）
以下， \{a_n\}, \{b_n\}, を数列とし，\displaystyle \alpha, \beta \in \mathbb{R}, \,\, \alpha=\lim_{n\to\infty} a_n, \, \beta=\lim_{n\to\infty} b_n とする。このとき，
- a_n = b_n \,\, (n\ge 1) ならば， \displaystyle \alpha = \beta である(極限の一意性)。
- \displaystyle \alpha + \beta = \lim_{n\to\infty} (a_n+b_n) . (和)
- \displaystyle \alpha\beta = \lim_{n\to\infty} a_nb_n . (積)
- \alpha \ne 0 ならば，\displaystyle \frac{\beta}{\alpha} = \lim_{n\to\infty} \frac{b_n}{a_n} . (商)
- a_n > 0 \,\,(n\ge 1) かつ \alpha = 0 ならば， \displaystyle \lim_{n\to\infty}\frac{1}{ a_n} = \infty . (商2)
- a_n \le b_n \,\,(n\ge 1) ならば， \alpha \le \beta . (大小関係の保存)
早速証明しましょう。
証明
証明する前に一つ注意ですが，以下の3つはどれを示しても， \lim_{n\to\infty} a_n = \alpha を示したことになります。
- 任意の \varepsilon > 0 に対し，ある N \ge 1 が存在して， n \ge N \implies | a_n - \alpha| < \varepsilon.
- 任意の \varepsilon > 0 に対し，ある N \ge 1 が存在して， n \ge N \implies | a_n - \alpha| < \textcolor{red}{\boldsymbol{k}} \varepsilon. ただし， k > 0 は N,\varepsilon に依存しない定数。
- 任意の 0<\varepsilon \textcolor{red}{\boldsymbol{< l}} に対し，ある N \ge 1 が存在して， n \ge N \implies | a_n - \alpha| < \varepsilon. ただし， l > 0 は N,\varepsilon に依存しない定数。
これが同値であることの説明については，イプシロンエヌ論法をわかりやすく丁寧に～数列の極限の定義～をみてください。
教科書に見かける証明の多くは，仮定に2.を使い，結論に1.(そして随時3.)が使われることが多いですが，「どうやってその定数思いついた？」なんてことがあるため，今回は逆で，仮定に1.をつかい，結論に2.を使う(そして随時3.を融合する)ことにします。
証明
\varepsilon > 0 を任意に取る。
すると，ある N_1, N_2 \ge 1 が存在して，
となる。さらに， N = \max\{N_1, N_2\} とする。これらを用いて順番に証明していこう。
1. a_n = b_n \,\, (n\ge 1) ならば， \displaystyle \alpha = \beta である(極限の一意性)。
a_n = b_n \,\, (n\ge N) と三角不等式により，
\begin{aligned}|\alpha - \beta| &\le |\alpha- a_N| + |a_N - \beta| \\ &< \varepsilon+\varepsilon = 2\varepsilon \end{aligned}
より，任意の \varepsilon > 0 に対し， |\alpha-\beta|< 2\varepsilon となるため， \alpha = \beta である。
2. \displaystyle \alpha + \beta = \lim_{n\to\infty} (a_n+b_n) . (和)
三角不等式により， n \ge N のとき，
\begin{aligned} |(a_n + b_n) - (\alpha + \beta)| &\le |a_n - \alpha| + |b_n-\beta| \\ &< \varepsilon + \varepsilon = 2\varepsilon \end{aligned}
より従う。
3. \displaystyle \alpha\beta = \lim_{n\to\infty} a_nb_n . (積)
0 < \varepsilon < 1 としておく。 n \ge N のとき，三角不等式より
\begin{aligned}|a_nb_n-\alpha\beta| &= |a_n(b_n-\beta) + \beta(a_n-\alpha) |\\ &\le |a_n||b_n-\beta| + |\beta||a_n-\alpha| \\ &< (|\alpha| + \varepsilon)\varepsilon + |\beta|\varepsilon \\ &< (|\alpha|+|\beta|+1)\varepsilon \end{aligned}
より従う。
4. \alpha \ne 0 ならば，\displaystyle \frac{\beta}{\alpha} = \lim_{n\to\infty} \frac{b_n}{a_n} . (商)
1/\alpha = \lim_{n\to\infty} 1/a_n を示せば，これと3.を使うことで結論が従うため，これを示す。
0<\varepsilon < |\alpha |/2 とすることで， |a_n - \alpha | < \varepsilon < |\alpha|/2. 特に， |a_n| > |\alpha|/2 > 0 が成り立つとしておく。すると
\begin{aligned} \left|\frac{1}{a_n} - \frac{1}{\alpha} \right| &= \frac{|\alpha-a_n|}{|a_n||\alpha|} \\ &< \frac{\varepsilon}{|\alpha|^2/2} = \frac{2}{|\alpha|^2} \varepsilon \end{aligned}
より示せた。
5. a_n > 0 \,\,(n\ge 1) かつ \alpha = 0 ならば， \displaystyle \lim_{n\to\infty}\frac{1}{ a_n} = \infty . (商2)
条件より， n \ge N \implies 0< a_n < \varepsilon であるため，
n \ge N \implies \frac{1}{a_n} > \frac{1}{\varepsilon }
である。これより結論が直ちに従う。
6. a_n \le b_n \,\,(n\ge 1) ならば， \alpha \le \beta . (大小関係の保存)
b_n - a_n \ge 0 より， n \ge N のとき，
\begin{aligned} \beta - \alpha &= (\beta - b_n) - (\alpha - a_n) + (b_n - a_n) \\ &\ge (\beta - b_n) - (\alpha - a_n) \\ &> -\varepsilon - \varepsilon = -2\varepsilon \end{aligned}
であり，任意の \varepsilon > 0 に対して， \beta-\alpha > -2\varepsilon が成立するから， \beta-\alpha \ge 0 である。
証明終
大小関係の保存に関する注意点
a_n \le b_n \,\, (n\ge 1) \implies \alpha \le \beta は正しいですが， a_n < b_n \,\, (n\ge 1) \implies \alpha < \beta は誤りです。
実際， a_n = 1/n とすると， a_n > 0 ですが，極限は \alpha =0 になるため， \alpha > 0 とはなりません。注意しましょう。
関数の極限の基本的な性質
関数に関しても，同じような性質が成立します。
定理（関数の極限の性質）
以下， f,g\colon \mathbb{R}\to\mathbb{R},\,\, -\infty \le a \le \infty とし，\displaystyle \alpha, \beta \in \mathbb{R}, \,\, \alpha=\lim_{x\to a} f(x), \, \beta=\lim_{x\to a} g(x) とする。このとき，
- f = g ならば， \displaystyle \alpha = \beta である(極限の一意性)。
- \displaystyle \alpha + \beta = \lim_{x\to a} (f(x)+g(x)) . (和)
- \displaystyle \alpha\beta = \lim_{x\to a} f(x)g(x) . (積)
- \alpha \ne 0 ならば，\displaystyle \frac{\beta}{\alpha} = \lim_{x\to a} \frac{g(x)}{f(x)} . (商)
- f(x)> 0 \,\,(x\ne a) かつ \alpha = 0 ならば， \displaystyle \lim_{x\to a}\frac{1}{f(x)} = \infty . (商2)
- f \le g \,\, (x\ne a) ならば， \alpha \le \beta . (大小関係の保存)
証明はほぼ同様（概ね n \ge N が 0<|x-a| < \delta に変わるだけ）なので，省略します。
その他の極限の性質
今回証明した以外にも，以下のような性質があります。
定理（数列の極限の性質2）
- \{a_n\} は有界，すなわち |a_n| < K \,\, (n\ge 1) となる K > 0 が存在する(有界性)。
- a_n \le c_n \le b_n \,\,(n\ge 1) かつ \displaystyle \alpha = \lim_{n\to\infty} a_n =\lim_{n\to\infty} b_n とすると， \displaystyle \lim_{n\to\infty} c_n = \alpha. (はさみうちの原理)
- a_n \le b_n \,\,(n\ge 1) かつ \displaystyle \lim_{n\to\infty} a_n = \infty とすると，\displaystyle \lim_{n\to\infty} b_n = \infty. (追い出しの原理)
- 上に有界な単調増加数列・下に有界な単調減少数列は収束する。(単調数列の収束)
- \displaystyle \alpha = \lim_{n\to\infty} a_n ならば，\displaystyle \alpha = \lim_{n\to\infty} \frac{a_1 + a_2 + \cdots +a_n}{n} . (平均値の収束)
1.から5.の証明は，それぞれ以下の記事を参照してください。
- 収束する数列は有界であることの証明
- はさみうちの原理とその厳密な証明～数列版・関数版～
- 追い出しの原理とその厳密な証明～数列版・関数版～
- 上に有界な単調増加数列は収束することの証明
- 【チェザロ平均】数列が収束するとき平均も同じ値に収束する証明
また，他にも以下のような記事があります。
