位相空間における局所連結とは,各点が連結な基本近傍系をもつことをいいます。連結であっても局所連結とは限らないし,局所連結であっても連結とは限りません。
局所連結の定義・具体例・性質を述べましょう。最後には,点ごとの局所連結・弱局所連結についても解説します。
局所連結の定義
連結の定義は既知とします(→位相空間における連結性について詳しく)。
定義1(局所連結)
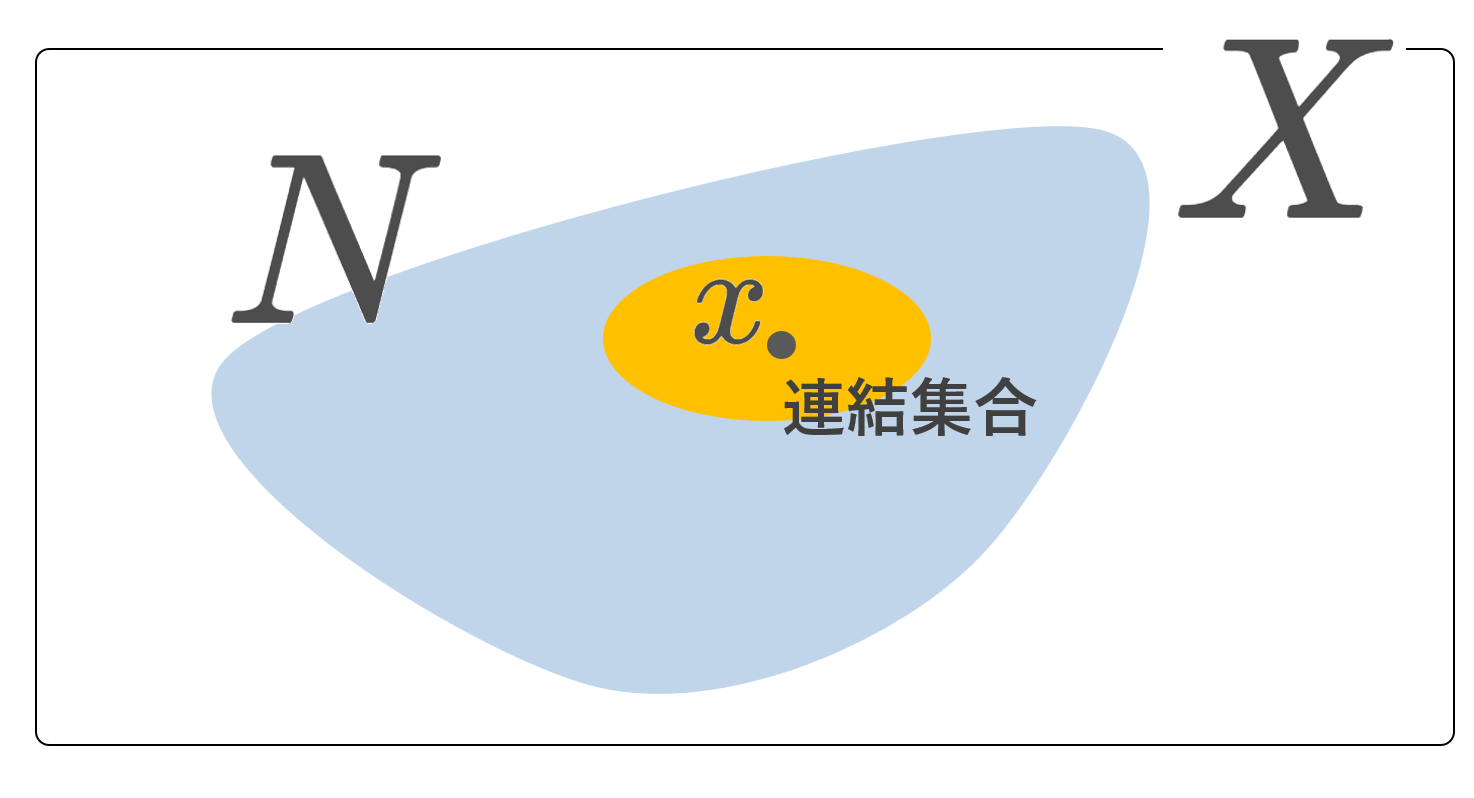
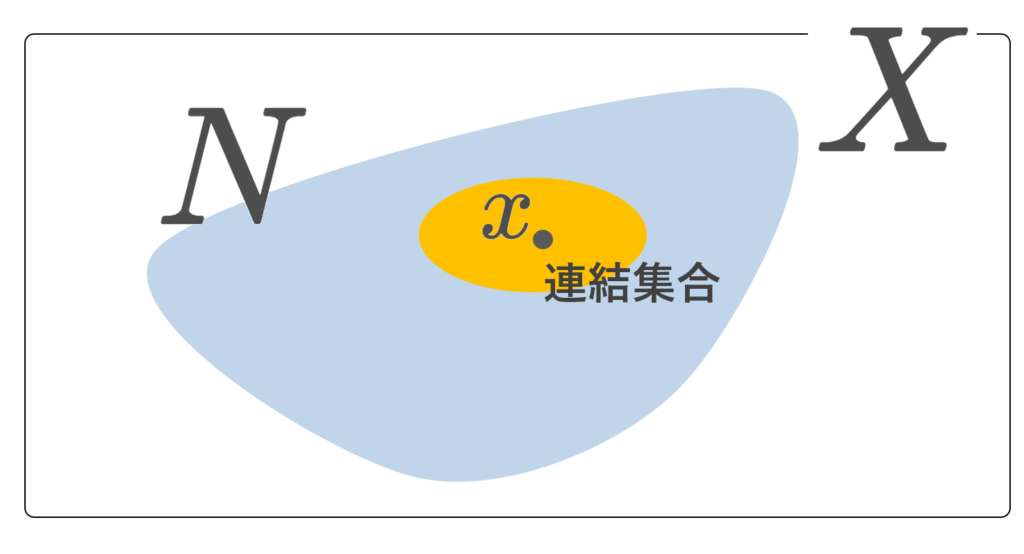
(X,\mathcal{O}) を位相空間とする。任意の x\in X に対し, x が連結集合からなる基本近傍系を持つとき, X は局所連結 (locally connected) であるという。
すなわち,任意の x\in X と x の任意の近傍 N に対し, x\in C\subset N かつ C は連結な x の近傍であるような C が取ってこれるような位相空間を局所連結というわけですね。
なお,連結性と局所連結性には関連性はなく,連結だが局所連結でない空間,局所連結だが連結でない空間の両方が存在します。具体例で紹介しましょう。
局所連結とそうでない具体例
連結性とも絡めながらみていきましょう。
例1(\R とその部分集合).
完全不連結とは,任意の連結成分が1点集合であるような位相空間のことです。
3.は,全体としてひとつながりではないので,連結ではありませんが,各点に対し,その点における十分小さい近傍を取ると,それは連結なので局所連結ではあります。
4.は,離散空間と同じです。例3.でも述べますが,離散空間においては1点集合が各点における連結成分であり,基本近傍系でもあるので局所連結です。
5.は完全不連結であることに加え,各点の近傍で連結であるものは存在しないので,局所連結にはなりません。
各点 x\in X の基本近傍系が \{X\} ですから,局所連結といえます。
各点 x\in X に対し,\{x\} が基本近傍系になりますから,局所連結です。
例4(位相幾何学者の正弦曲線).
\R^2 の部分集合
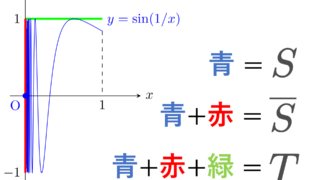
S=\left\{\left(x, \sin\frac{1}{x}\right)\middle| 0<x\le 1\right\}\cup \{(0,0)\}
とすると,その閉包は \overline{S} = S\cup \left(\{0\}\times [-1,1]\right) となる。
さらに, T=\overline{S}\cup \left([0,1]\times \{1\}\right) とする。
このとき, S,T は連結・弧状連結・弧連結である。\overline{S} は連結だが,弧状連結・弧連結ではない。
また, S,\overline{S}, T はどれも局所連結ではない。
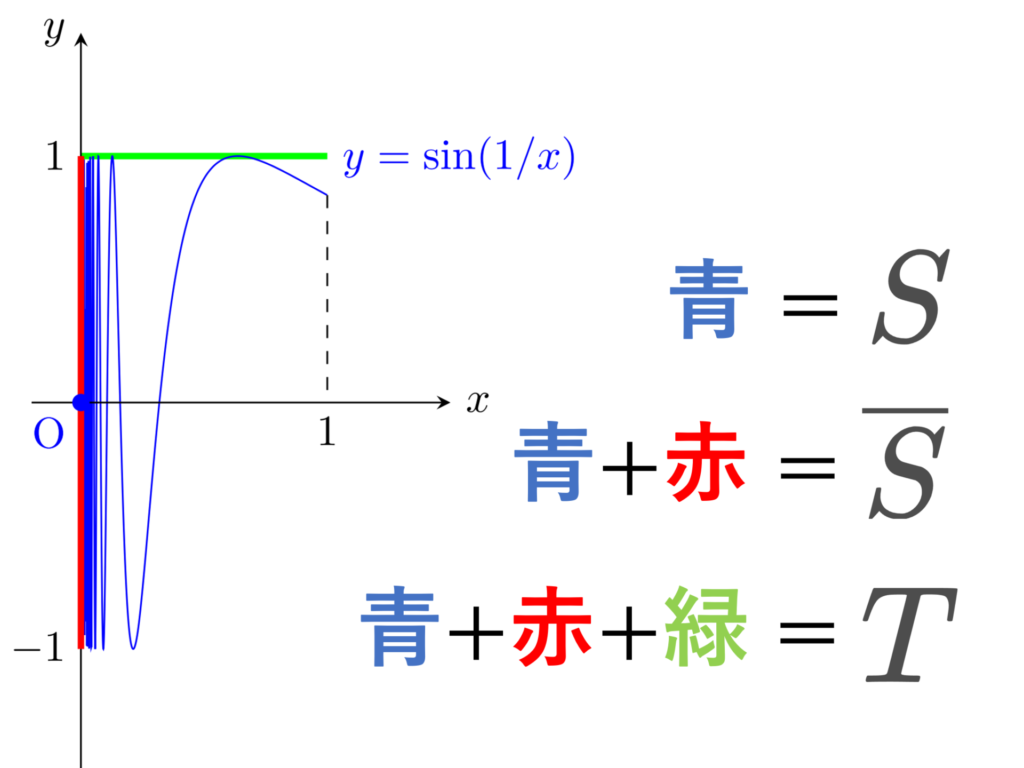
これは,連結だが弧状連結でない典型例として述べられることが多いですが,局所連結でもありません。たとえば,原点まわりの \varepsilon –近傍を考えると,これは連結集合ではありません。
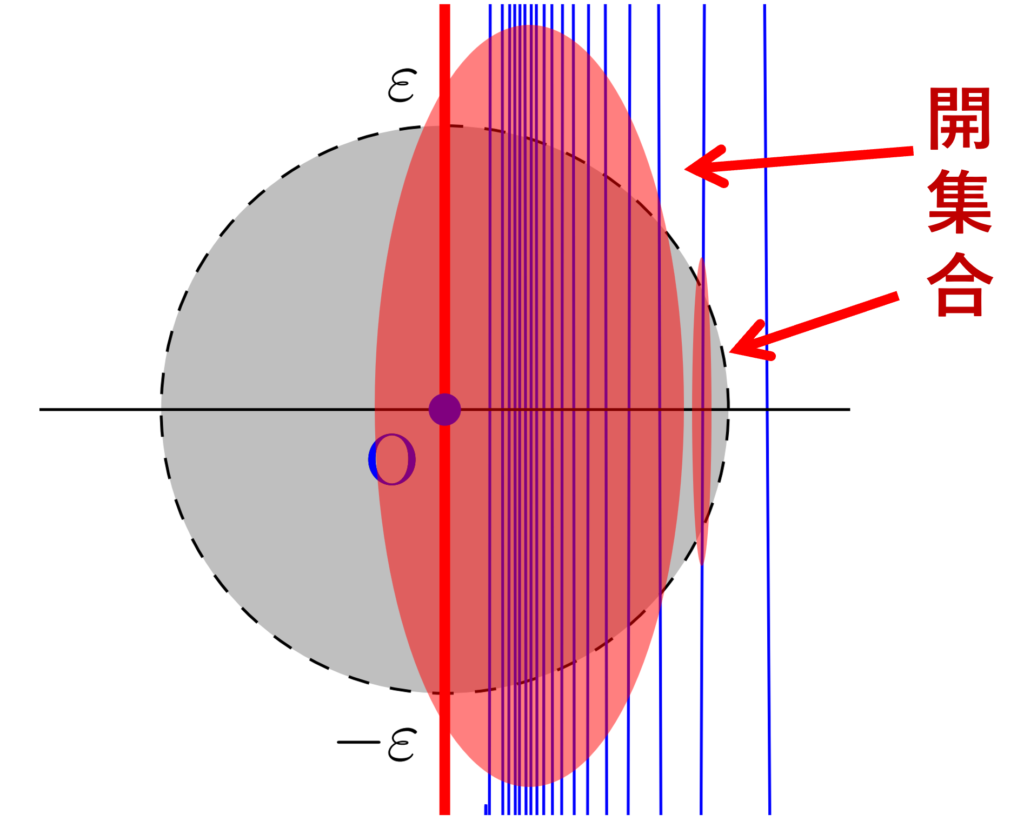
この空間の解説は,以下の記事で行っています。
類例として,くし空間 (comb space) というのもあります。【位相空間】くし空間(Comb Space)で解説しています。また,ほうき空間 (broom space) も知られています(→【位相空間】ほうき空間(Broom Space))。
局所連結の性質
性質を2つ紹介します。
1. 局所連結と同値な性質
定理1(局所連結と同値な性質)
(X,\mathcal{O}) を位相空間とする。このとき,以下は同値である。
- X は局所連結である。すなわち,任意の x\in X に対し, x が連結集合からなる基本近傍系を持つ
- 任意の x\in X に対し, x が連結開集合からなる基本近傍系を持つ
- X の任意の開部分空間の任意の連結成分は開集合である
- X の連結な開集合全体が位相 \mathcal{O} の開基になる
また,3.と連結成分は常に閉集合であることより,X が局所連結ならば, X の任意の連結成分は開かつ閉である。
同値性を証明しましょう。
同値性の証明
4. \implies 2. \implies 1.は明らか。
以下 A\subset X に対し,部分空間 A における x\in A の連結成分を C_A(x) と表すことにする。
1. \implies 3.について
U\subset X を開集合とし, x\in U とする。 C_U(x)\subset U が開集合であることを示そう( U\subset X は開集合なので, U におけるの開集合 \iff X における開集合であることに注意)。
y\in C_U(x)\subset U とすると,U は開集合なので,1.より y\in V\subset U となる連結な近傍 V が存在する。 C_U(x) は,y を含む U における最大の連結集合なので, V\subset C_U(x) である。特に C_U(x) は y の近傍であるから, C_U(x) は開集合である。
3.\implies 4.について
U\subset X を任意の開集合とすると,
U=\bigcup_{x\in U} C_U(x)
であり,3.より, C_U(x) は連結な開集合なので,連結な開集合全体が開基になっている。
証明終
2. 局所連結性と商位相
定理2(局所連結性と商位相)
(X,\mathcal{O}) を位相空間とし,\sim をその上の同値関係, X/\sim を商空間とする。
このとき, X が局所連結ならば, X/\sim も局所連結である。
以下,\pi\colon X\to X/\sim を自然な射影とします。商位相で大事なのは, V\subset X/\sim が開 \iff \pi^{-1}(V)\subset X が開が成り立つことです(→商位相と商写像)。
証明
V\subset X/\sim を開集合とし, y\in V とする。定理1より, y の V における連結成分 C_V(y) が開であることを示せばよい。
x\in \pi^{-1}(C_V(y))\subset \pi^{-1} (V) とすると, \pi は連続なので \pi^{-1}(V) は開集合であり,ゆえに X の局所連結性と定理1から x\in C\subset \pi^{-1}(V) となる連結開集合 C\subset X が存在する。
連結集合の連続像は連結なので,\pi(C) は連結集合である。また, \pi(x)\in\pi(C)\subset V であり, \pi(x)\in C_V(y), C_V(y) は x を含む最大の連結集合でもあるから,\pi(x)\in \pi(C)\subset C_V(y) である。
よって, x\in C\subset \pi^{-1}(C_V(y)) となるが, C は開集合なので, \pi^{-1}(C_V(y)) は x の近傍である。 x\in \pi^{-1}(C_V(y)) の取り方は任意だったから,\pi^{-1}(C_V(y)) は開集合である。よって証明直前に述べたことにより, C_V(y) は開集合である。
証明終
なお,一般に位相空間 X,Y と連続写像 f\colon X\to Y に対し, X が局所連結だからと言って, f(X) が局所連結にはなりません。これは連結性や弧状連結性とは対照的な性質です。
たとえば, (X,\mathcal{O}) を局所連結でない位相空間とし, (X,2^X) を,位相を離散位相に変えたものとすると,恒等写像 \operatorname{id}\colon (X, 2^X)\to (X,\mathcal{O}) は連続かつ,定義域は局所連結ですが,像は局所連結ではありません。
各点ごとの局所連結と弱局所連結
位相空間として局所連結の話をしてきましたが,局所連結性は各点で定義することも可能です。考えてみましょう。
定義2(各点ごとの局所連結・弱局所連結)
(X,\mathcal{O}) を位相空間とし, x\in X とする。
定義1より,位相空間が局所連結であるとは,各点において弱局所連結が成立することであり,定理1より,これは各点において局所連結が成立することと同値です。
しかし,位相空間として局所連結でないときは,ある点で弱局所連結だが局所連結でないようにすることができます。たとえば,以下のような閉ほうき空間 (closed infinite broom, closed broom space) を考えます。これは \R^2 において,各 n=1,2,3,\ldots に対し,原点と (1, 1/n) を結ぶ線分と,原点と (1,0) を結ぶ線分を考えた位相空間です。
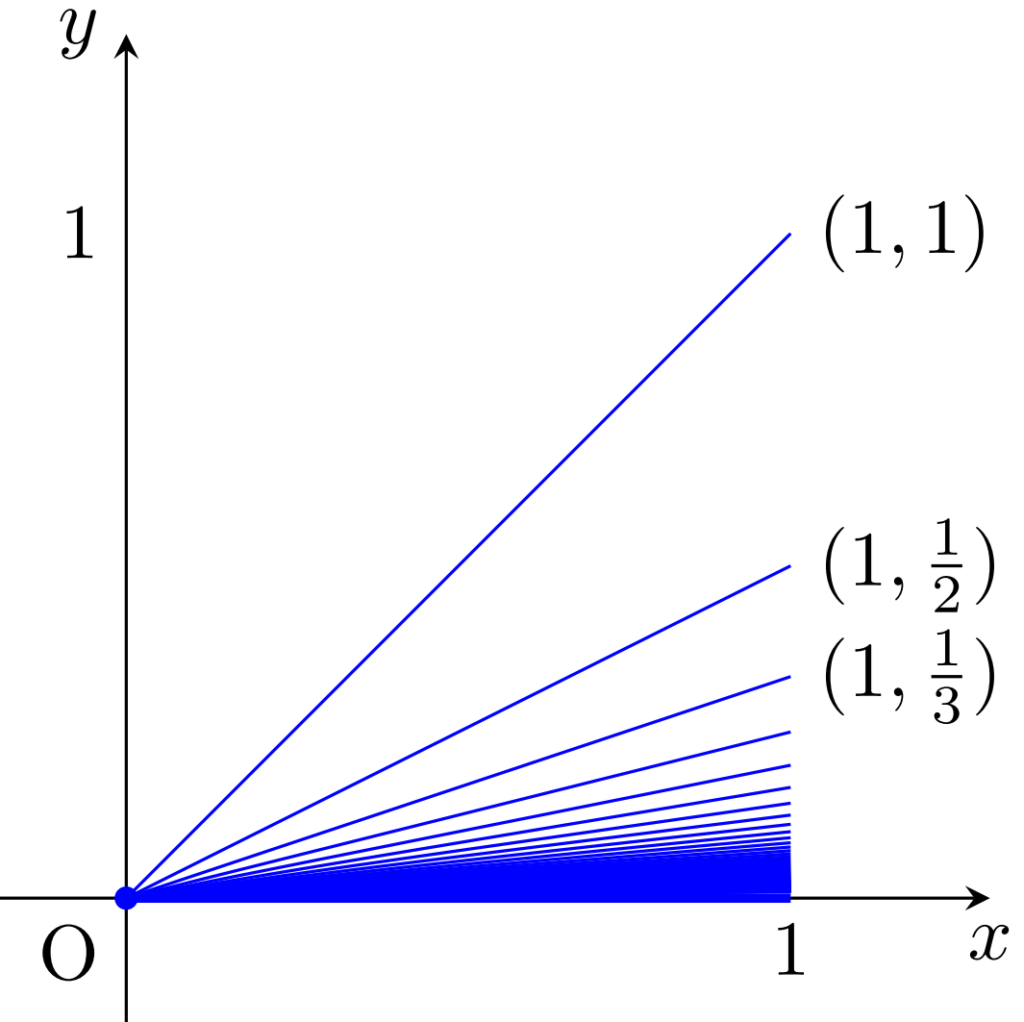
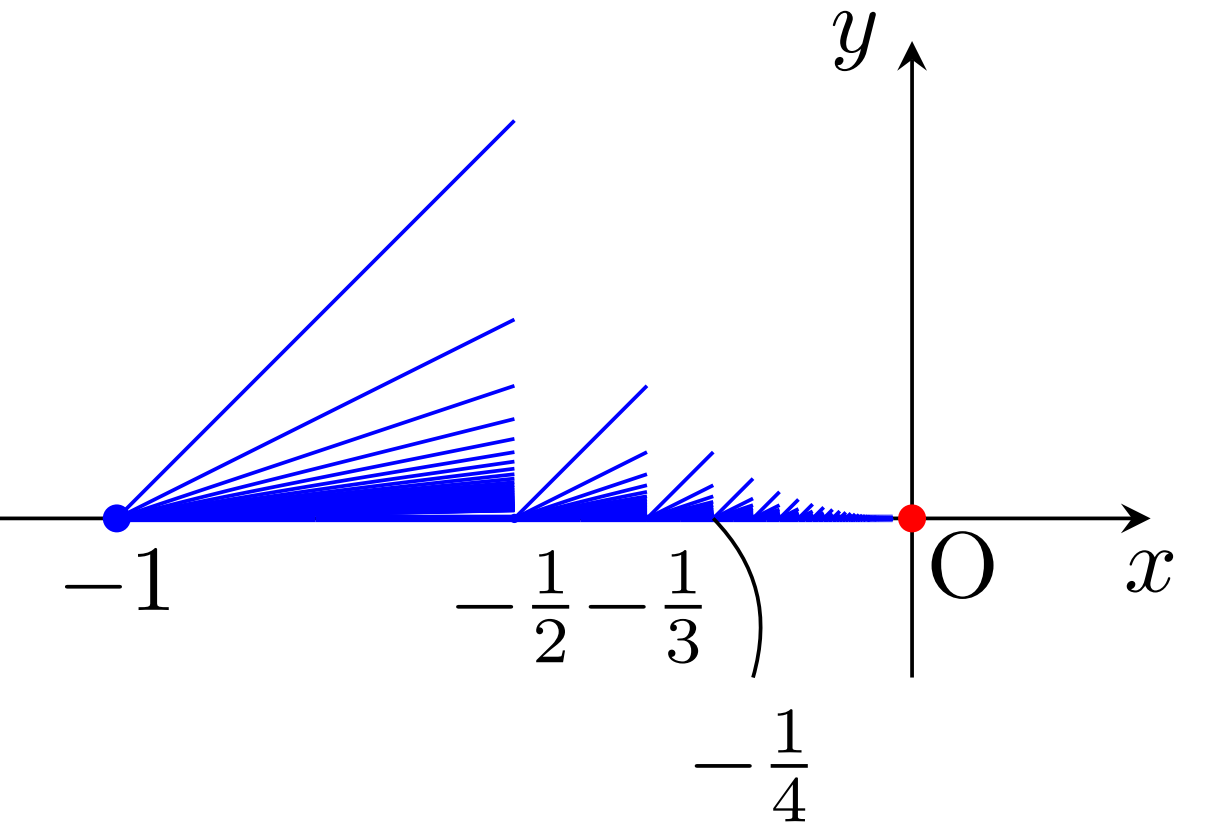
さらに,閉ほうき空間を下図のように縮小・平行移動して無限個貼り合わせ,さらに原点を合わせた位相空間 B_\infty を考えます。
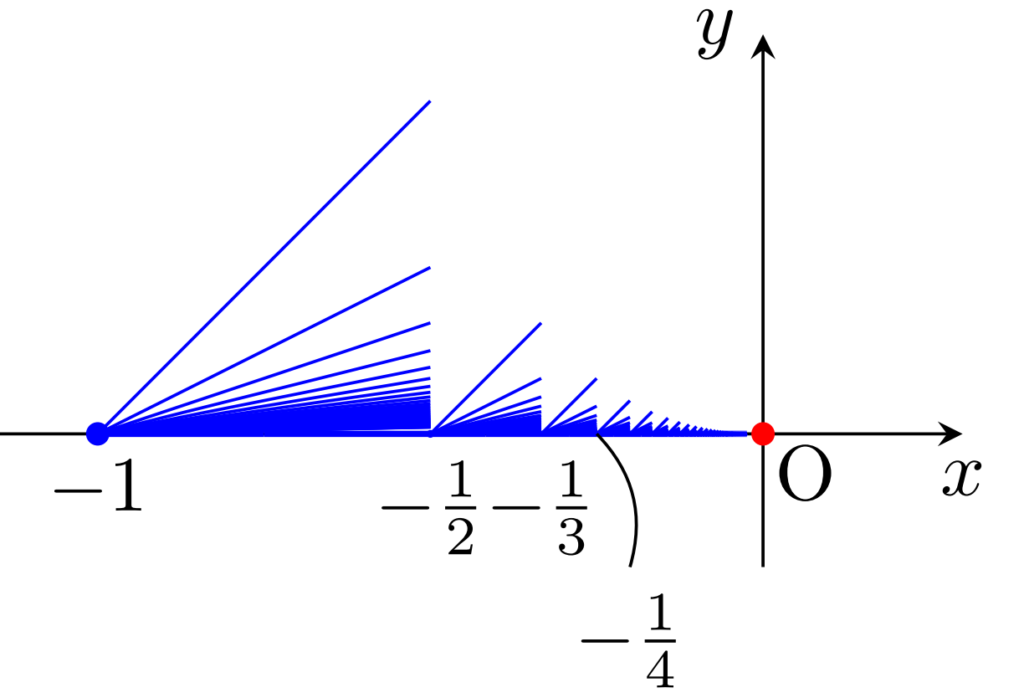
この場合,原点の開近傍で連結なものは存在しないため,原点において局所連結ではありません。一方で, n\ge 1 に対し,
\overline{B_\infty}\cap \{(x,y)\in\R^2 \mid x\ge -1/n\}
は原点における基本近傍系になっているので,原点において弱局所連結です。ほうき空間・閉ほうき空間については,以下で詳しく解説しています。
連結性に関連する概念
| 名称 | 定義 |
|---|---|
| 連結 (connected) | 2つの互いに素な空でない開集合 U,V で, U\cup V=X となっているものは存在しない |
| 弧状連結 (path connected) | 任意の異なる2点 x,y\in X について,ある連続写像 f\colon [0,1]\to X で, f(0)=x, f(1)=y となるものが存在する |
| 弧連結 (arc connected) | 上の f として,埋め込みすなわち f\colon [0,1]\to f([0,1]) が同相となっているものが常に取れる(※[2]では単に全単射なものが取れるとしている。 X がハウスドルフ ( T_2)なら弧状連結と弧連結は同値) |
| hyperconnected | 任意の空でない2つの開集合が常に共通部分を持つ |
| ultraconnected | 任意の空でない2つの閉集合が常に共通部分を持つ |
| 完全不連結 (totally disconnected) | 連結部分集合が1点集合のみ |
| 完全弧状不連結 (totally path disconnected) | 弧状連結部分集合が1点集合のみ |
| 局所連結 (locally connected) | 全ての点において,連結集合からなる基本近傍系を持つ |
| 局所弧状連結 (locally path connected) | 全ての点において,弧状連結集合からなる基本近傍系を持つ |
| 単連結 (simply connected) | f(0)=f(1) をみたす任意の連続写像 f\colon [0,1]\to X が定値写像とホモトピック |