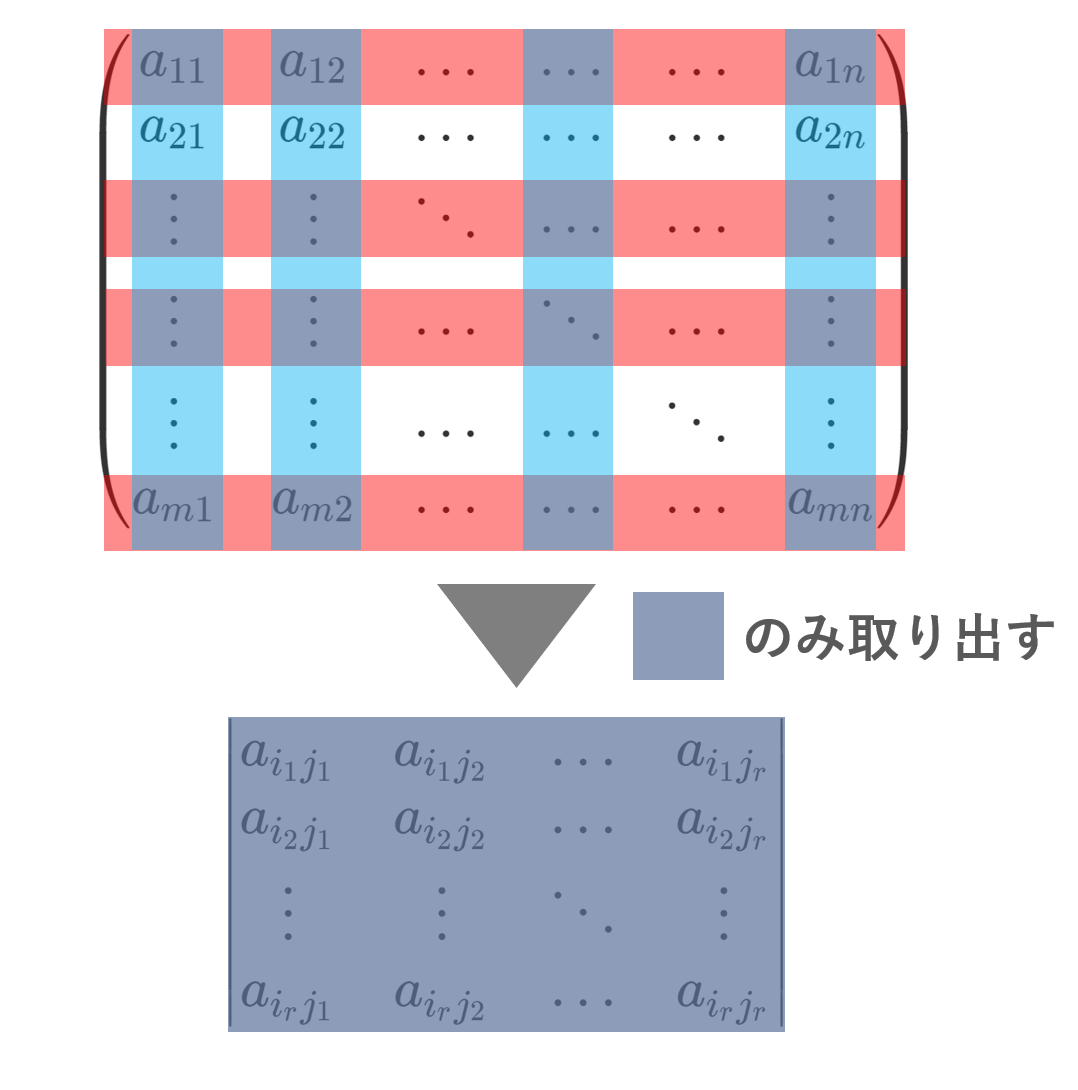
m\times n 行列における小行列式とは,元の行列から行・列を同じ数だけ選んで,それのみ並べ直した r 次正方行列の行列式(det)のことを指します。このことについて,定義と,元の行列の階数(ランク)との関係,また余因子との関係も述べましょう。
小行列式の定義と例
定義(小行列式)
A =(a_{ij}) を m\times n 行列とする。 1\le r\le \min\{m,n \} とし, A から r 個の行 i_1, i_2,\dots, i_r と r 個の列 j_1,j_2,\dots,j_r を選んで作った r 次正方行列(小行列という)の行列式
\color{red} \begin{vmatrix} a_{i_1j_1}&a_{i_1j_2}&\dots & a_{i_1j_r} \\ a_{i_2j_1} & a_{i_2j_2}&\dots& a_{i_2j_r} \\ \vdots & \vdots &\ddots & \vdots \\ a_{i_rj_1} & a_{i_rj_2}& \dots & a_{i_rj_r} \end{vmatrix}
を A の r 次の小行列式 (minor determinant) という。
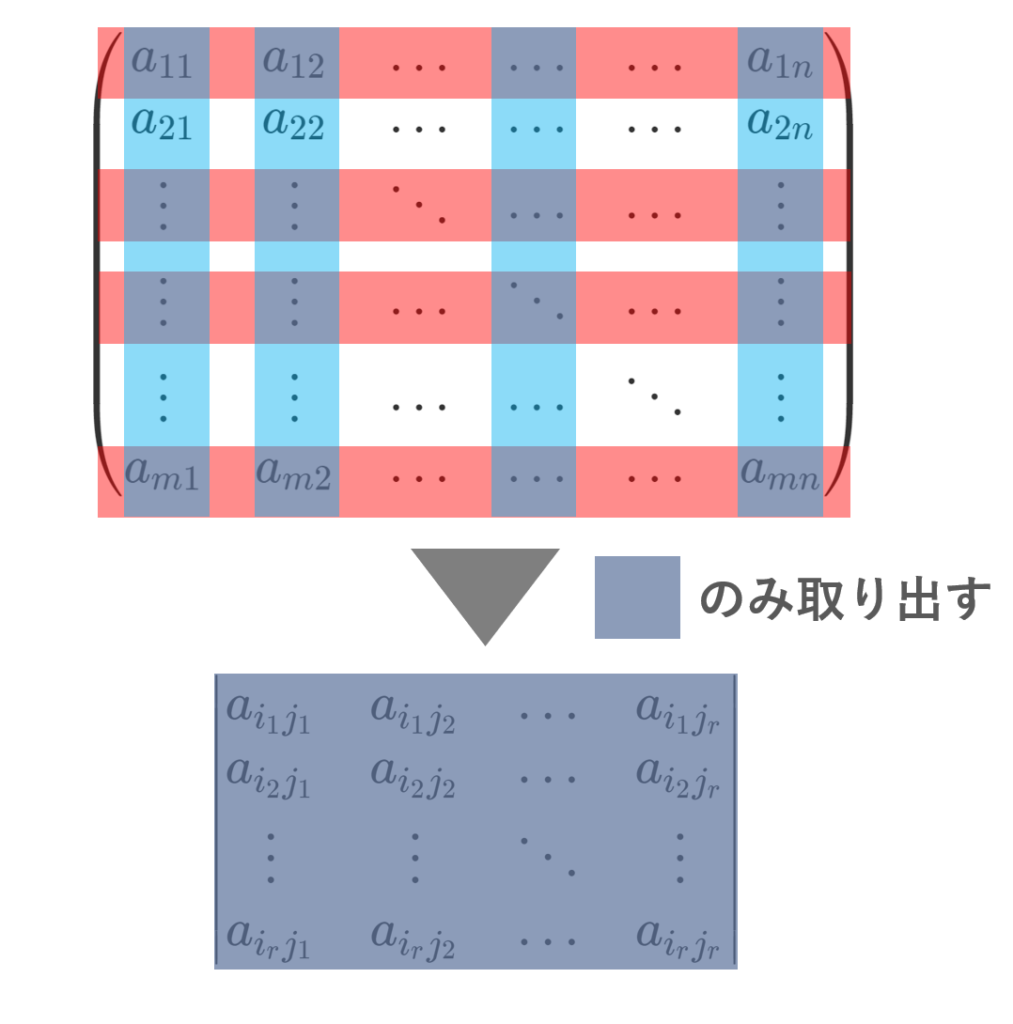
元の行列から部分的に行・列を取り出し,その行列式を考えるということですね。
例を一つ挙げましょう。
小行列式の例
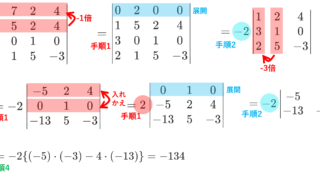
\begin{pmatrix} 1& 2& 3 \\ 4 & 5 & 6 \\ 7& 8& 9 \end{pmatrix} の第 1,2 行,第 1,3 列を取り出した小行列式は
\begin{vmatrix}1& 3 \\ 4 & 6 \end{vmatrix} = 1\cdot 6-3\cdot 4 = -6
である。
小行列式と階数(ランク)
小行列式と元の行列の階数(ランク)については,以下のような関係があります。
定理(小行列式と階数(ランク))
A を m\times n 行列, r=\operatorname{rank} A とする。このとき, A の s 次の小行列式で 0 でないものが存在する必要十分条件は s\le r である。
簡潔ですが証明しましょう。
証明
\implies について
対偶を示す。 s> r とすると, s 次の小行列 B の階数は高々 r である。 \det B \ne 0 \iff \operatorname{rank} B = s であるから, \det B = 0 である。
\impliedby について
s\le r とすると, A の行ベクトルから s 個の一次独立なベクトルが取れる。この s\times n 行列の階数は s である。この行列から,一次独立な列ベクトルが s 個取れる。この s\times s 行列の階数は s であるから,この小行列式は 0 でない。
証明終
小行列式と余因子
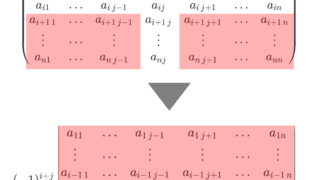
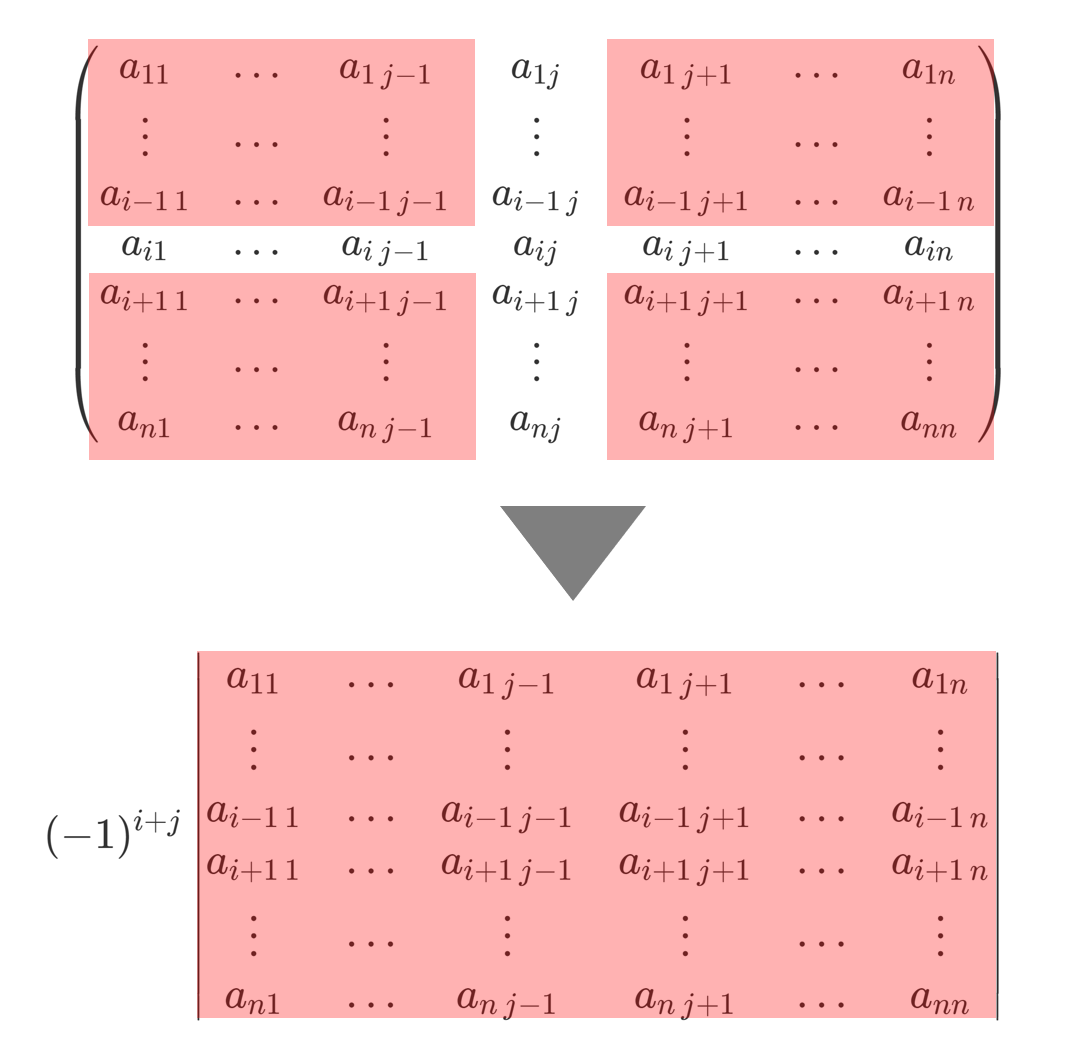
n 次正方行列において,第 i 行・第 j 列を除いて残りの n-1 個を並べて作った n-1 次正方行列の小行列式
\small \begin{vmatrix} a_{11} & \dots & a_{1\,j-1} & a_{1\,j+1} &\dots & a_{1n} \\ \vdots & \cdots & \vdots & \vdots & \cdots & \vdots \\ a_{i-1\,1} & \dots & a_{i-1\,j-1} & a_{i-1\,j+1} &\dots & a_{i-1\,n}\\ a_{i+1\,1} & \dots & a_{i+1\,j-1} & a_{i+1\,j+1} &\dots & a_{i+1\,n}\\ \vdots & \cdots & \vdots & \vdots & \cdots & \vdots \\ a_{n1} & \dots & a_{n\,j-1} & a_{n\,j+1} &\dots & a_{nn} \end{vmatrix}
に対し,その (-1)^{i+j} 倍した
を A の (i,j) 余因子 (cofactor) といいます。余因子については,良い性質があります。以下の記事で解説しましょう。