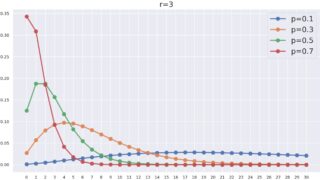
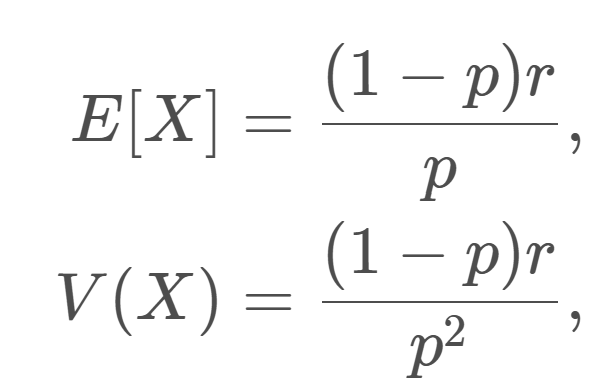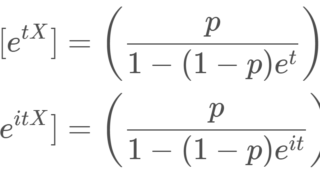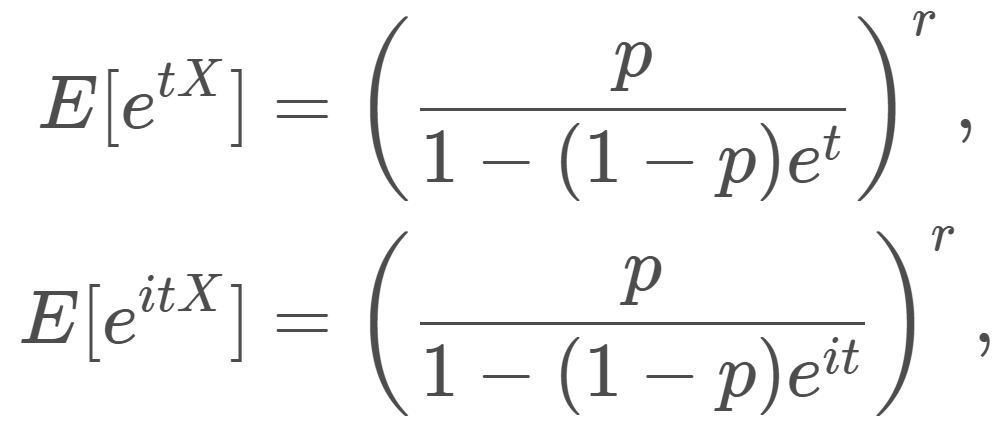負の二項分布 NB(r,p) について,その期待値(平均)・分散・標準偏差はそれぞれ
\begin{aligned} E[X] &= \dfrac{(1-p)r}{p},\\ V(X)&= \dfrac{(1-p)r}{p^2},\\ \sqrt{V(X)}&= \dfrac{\sqrt{(1-p)r}}{p} \end{aligned}
となります。これについて「直接証明する方法」「特性関数の微分を用いる方法」の2通りで証明しましょう。
負の二項分布の期待値(平均)・分散・標準偏差
定理(負の二項分布の期待値(平均)・分散・標準偏差)
X\sim NB(r, p) とする。このとき, X の期待値(平均)・分散・標準偏差は
\color{red} \begin{aligned} E[X] &= \dfrac{(1-p)r}{p},\\ V(X)&= \dfrac{(1-p)r}{p^2},\\ \sqrt{V(X)}&= \dfrac{\sqrt{(1-p)r}}{p} \end{aligned}
である。
証明に入る前に,負の二項分布の復習をしておきます。
0<p<1, \, r\ge 1 を整数とする。確率変数 X が k = 0,1,2,\ldots に対し,
\color{red}\begin{aligned} P(X=k) &= {}_{k+r-1}\mathrm{C}_k\, p^r(1-p)^k \\ &= {}_{k+r-1}\mathrm{C}_{r-1}\, p^r(1-p)^k \end{aligned}
となるとき, X はパラメータ (r, p) の負の二項分布 (negative binomial distribution) に従うという。本記事では,\color{red} X\sim NB(r,p) とかくことにする。
負の二項分布全般の性質については,以下でまとめています。
負の二項分布の期待値(平均)の導出証明
さて,早速進めていきます。
- 定義から直接証明する方法
- 特性関数の微分を用いる方法
の2通りで証明しましょう。
【期待値】定義から直接証明する方法
証明
期待値の定義より,
\begin{aligned} E[X]&= \sum_{k=0}^\infty k P(X=k) \\ &= \sum_{k=0}^\infty k \,{}_{k+r-1}\mathrm{C}_{k}\, p^r(1-p)^k \\ &= \sum_{k=1}^\infty k \,{}_{k+r-1}\mathrm{C}_{k}\, p^r(1-p)^k. \end{aligned}
ここで, k\ge 1 のとき
であるから,
である。ただし, Y\sim NB(r+1, p) と定めた。以上から, E[X] = \dfrac{(1-p)r}{p} .
証明終
【期待値】特性関数の微分を用いた方法
特性関数の微分を用いる方法を証明する前に,負の二項分布の特性関数を確認しておきます。
証明
特性関数の両辺を t で微分すると,
\small E[iXe^{itX}] = \frac{i(1-p)re^{it}}{1-(1-p)pe^{it}} \left(\dfrac{p}{1-(1-p)e^{it}}\right)^{r}両辺 t=0 を代入すると,
E[iX] = \frac{i(1-p)r}{p}
であるから, E[X] = \dfrac{(1-p)r}{p} .
証明終
なお,今回は特性関数を用いましたが,積率母関数(モーメント母関数)を用いても,同様に証明できます。
負の二項分布の分散の導出証明
さて,分散の証明も,
- 定義から直接証明する方法
- 特性関数の微分を用いる方法
の2通りで証明しましょう。 V(X) = E[X^2] - E[X]^2 を用います。
【分散】定義から直接証明する方法
証明
まず,期待値の2次モーメントについて,
\small \begin{aligned} &E[X^2] \\ &= \sum_{k=0}^\infty k^2 P(X=k) \\ &= \sum_{k=0}^\infty k^2 \,{}_{k+r-1}\mathrm{C}_{k}\, p^r(1-p)^k \\ &= \sum_{k=2}^\infty k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\, p^r(1-p)^k \\ &\quad + \sum_{k=1}^\infty k \,{}_{k+r-1}\mathrm{C}_{k}\, p^r(1-p)^k \\ &= \sum_{k=2}^\infty k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\, p^r(1-p)^k + E[X] \\ &= \sum_{k=2}^\infty k(k-1) \,{}_{k+r-1}\mathrm{C}_{k}\, p^r(1-p)^k + \dfrac{(1-p)r}{p} \end{aligned}
である。ここで, k\ge 2 のとき,
であるから,
ただし, Z\sim NB(r+2 ,p) とした。よって,
なので,
証明終
【分散】特性関数の微分を用いる方法
証明
特性関数の式 E[e^{itX}]=\left(\dfrac{p}{1-(1-p)e^{it}}\right)^r,\quad t\in\mathbb{R} の両辺 t で2回微分すると,
\small \begin{aligned}&E[(iX)^2e^{itX}] \\ &= - \frac{(1-p)re^{it}\{1+(1-p)re^{it}\}}{\{1-(1-p)e^{it}\}^2} \left(\dfrac{p}{1-(1-p)e^{it}}\right)^r \end{aligned}
となる。両辺 t=0 を代入して -1 倍すると,
したがって,
証明終
負の二項分布の標準偏差について
標準偏差は,分散の平方根 \sqrt{V(X)} でしたから,上で分散を求めたことで,
\sqrt{V(X)} = \frac{\sqrt{(1-p)r}}{p}
と求まりますね。